図形の回転は、すべてが同じ角度で回転する～～

図形を回転させるとき、どこを回転の中心にしても

中心と各頂点でできる線の 回転角度は どの頂点においても

同じ角度だけ 回転します。

また、その時  回転前と 回転後の 各辺がつくる角度も 同じになります。

ここで、どうしてみんな同じ角度になるのか？ということを

納得できるまで じっくり説明してもらえる場が、学校の授業だといいのですが

これがなかなか難しいようで、できない場合が多いようです。

 

今回は、この図形の回転の性質を使います。

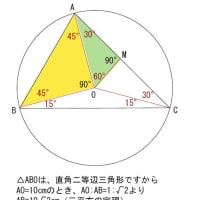
前回の問題で、図の中に

Aを 回転の中心とした

回転前の三角形（黄色）と回転後の三角形（緑色）を考えます。

黄色の三角形で辺AEは、緑色の三角形辺ABまで回転します。

これは△ADBが正三角形だから回転した角度は６０°

同じように、黄色の三角形の辺ACは 緑色の三角形の辺AEまで回転します。

これも△ACEが正三角形だから回転した角度は６０°

回転前の図形と 回転後の図形がぴったり重なりますので

これはたしかに緑色の三角形は、黄色の三角形が６０°回転した図形です。

これで、辺DCと 辺BEは 回転前の辺と 回転後の辺になりますので

これも回転角度は ６０°  Xは６０° です。

 

問題の中にかかれてある６５°の角度は回転には関係のない角度でした。

ここは何度であっても、Xに影響しませんね。