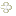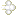どもども。
今回は前回に引き続き,2012年東大入試理系数学第5問をやってみたいと思います
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon5.html
前回は主に行列の累乗を求める話をやっていて(2)がまだ途中でした。
上手にkを取ると,B^kA または {B^(-1)}^kA が与えられた4つの行列に
等しくすることができる,ということを確かめる問題です。
このB^kA と {B^(-1)}^k を求めるところまで話が済んでいます。
まぁ,残りはただのやっつけ仕事なんですが
さて,ad-bc=0,c=0 という情報が与えられています。
このことより,(a,d)=(1,1)=(-1,-1)の2パターンに絞られるわけなので
まずはdの値が1か-1かで分けて考えてみます。
右上の成分のみがkによって変動し,それが0になるときを選べばOKです

与えられた4つの行列に右からAの逆行列をかけたもののいずれかが
BまたはB^(-1)の累乗の形になることを確かめるのもよいです。

(3)をみてみます。問題文はゴチャゴチャ書いてますが
早い話が, |a+c|<|a| か,或いは |a-c|<|a| かどちらかは成り立つことを
確かめる問題です。シンプルな話なので説明の仕方は色々あるでしょう。
±cの存在範囲は -|a|≦|c|≦|a|,c≠0 より
半開区間 [-|a|,0) または (0,|a|] です。
|a+c|は点cと点-aの距離,|a-c|は点cと点aの距離を表します。
cはaか-aかどちらかと同符号ですが,点cとその同符号の方の点との距離が|a|より小さいわけであります

|a+c|<|a| か,或いは |a-c|<|a| かを示すわけですが,
非負実数の大小比較なので,2乗の大小関係で比較してもいいです。

cは整数であるという仮定ですが,これを連続変数と思って
cの関数 f(c)=|a|-|a+c| と g(c)=|a|-|a-c| を考える作戦もあります。
このときaは固定して定数だとみなして考えるわけですね

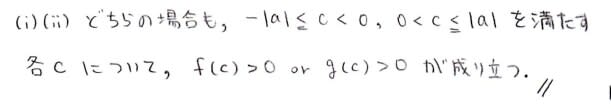
一般に,X,Y≠0のとき,XY<0が成り立つなら
X,Yは異符号でどちらか一方は正,もう一方は負です。
|a|>|a+c|のとき|a|<|a-c|となることが図から分かると思います。
(|a|-|a+c|)×(|a|-|a-c|)<0を示せば
|a|>|a+c| か |a|>|a-c|が成り立つことがいえます。
下の解法ではcを変数として扱ってますが,わざわざそんな事しなくても
良さそうですね。

さて,上の解法に関連した別解法としては次のような方針もあります。
点cと点aの距離をL,点cと点-aの距離をMとおくと
L+M=2|a|になってることが数直線から分かるはずです。
つまり|a+c|+|a-c|=2|a|です。これを移項すれば
|a+c|-|a|=|a|-|a-c|となります。
この式より,|a|-|a+c|と|a|-|a-c|が異符合であることが分かるので
|a|>|a+c| か |a|>|a-c|が成り立つことがいえます
今回は前回に引き続き,2012年東大入試理系数学第5問をやってみたいと思います

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon5.html
前回は主に行列の累乗を求める話をやっていて(2)がまだ途中でした。
上手にkを取ると,B^kA または {B^(-1)}^kA が与えられた4つの行列に
等しくすることができる,ということを確かめる問題です。
このB^kA と {B^(-1)}^k を求めるところまで話が済んでいます。
まぁ,残りはただのやっつけ仕事なんですが

さて,ad-bc=0,c=0 という情報が与えられています。
このことより,(a,d)=(1,1)=(-1,-1)の2パターンに絞られるわけなので
まずはdの値が1か-1かで分けて考えてみます。
右上の成分のみがkによって変動し,それが0になるときを選べばOKです


与えられた4つの行列に右からAの逆行列をかけたもののいずれかが
BまたはB^(-1)の累乗の形になることを確かめるのもよいです。

(3)をみてみます。問題文はゴチャゴチャ書いてますが
早い話が, |a+c|<|a| か,或いは |a-c|<|a| かどちらかは成り立つことを
確かめる問題です。シンプルな話なので説明の仕方は色々あるでしょう。
±cの存在範囲は -|a|≦|c|≦|a|,c≠0 より
半開区間 [-|a|,0) または (0,|a|] です。
|a+c|は点cと点-aの距離,|a-c|は点cと点aの距離を表します。
cはaか-aかどちらかと同符号ですが,点cとその同符号の方の点との距離が|a|より小さいわけであります


|a+c|<|a| か,或いは |a-c|<|a| かを示すわけですが,
非負実数の大小比較なので,2乗の大小関係で比較してもいいです。

cは整数であるという仮定ですが,これを連続変数と思って
cの関数 f(c)=|a|-|a+c| と g(c)=|a|-|a-c| を考える作戦もあります。
このときaは固定して定数だとみなして考えるわけですね


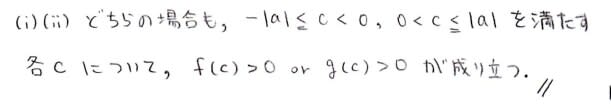
一般に,X,Y≠0のとき,XY<0が成り立つなら
X,Yは異符号でどちらか一方は正,もう一方は負です。
|a|>|a+c|のとき|a|<|a-c|となることが図から分かると思います。
(|a|-|a+c|)×(|a|-|a-c|)<0を示せば
|a|>|a+c| か |a|>|a-c|が成り立つことがいえます。
下の解法ではcを変数として扱ってますが,わざわざそんな事しなくても
良さそうですね。

さて,上の解法に関連した別解法としては次のような方針もあります。
点cと点aの距離をL,点cと点-aの距離をMとおくと
L+M=2|a|になってることが数直線から分かるはずです。
つまり|a+c|+|a-c|=2|a|です。これを移項すれば
|a+c|-|a|=|a|-|a-c|となります。
この式より,|a|-|a+c|と|a|-|a-c|が異符合であることが分かるので
|a|>|a+c| か |a|>|a-c|が成り立つことがいえます

















 ということを証明してくれという問題です。
ということを証明してくれという問題です。