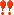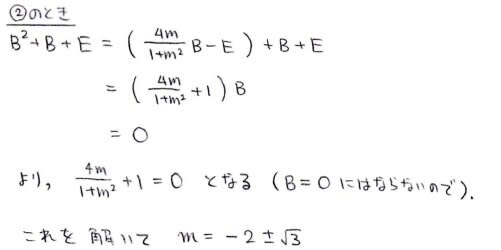どもども。
今回は今年の東北大入試理系数学の第5問をやっていきます~

問題はこちら


まぁ早い話が上の図において,(1)yをxの式で表せ (2)yが最大のときのxは?
という問題です
図形的な問題なので様々な解法があるでしょう。
後半は微分です
今年の東大入試第1問に似た雰囲気があります
yをxの式で表すよう指示しておきながら,xの関数と思って微分するより
角度を変数として微分するほうが簡単といういやらしさがあります~
それではやっていきましょう~
 △PBQで正弦定理を使うパターン
△PBQで正弦定理を使うパターン
まずは一番手っ取り早そうな解法からいきます~
△PBQは2辺の長さがx,yになってるので,なんか正弦定理とか使うとうまくいきそうですね
円の中心をO,∠PBQ=θ(0<θ<π/2)とおいておきます。
ABは円の直径なので∠APBは直角です。△APBに着目するとx=cosθであることが分かります
0<θ<π/2 なので sinθ>0 ですから,sinθ=√(1-x^2)です。
これでxとθを結ぶ関係が得られましたね


答えの式がなかなか複雑です
どこまで計算して“答え”とするかは悩みどころですが,
(2)を見れば分かるようにyが最大のときのxを求めるのがこの問題の趣旨のようなので
(1)に関しては答えの形に関してはあまり気にしなくてもよさそうです
ただ,yをどのような形で表示するかによって(2)の計算の面倒さなどには影響は与えそうです。
 △PBQで余弦定理を使うパターン
△PBQで余弦定理を使うパターン
正弦定理を使う解法があるなら余弦定理を使う解法だってあるだろう~
ってことで今度は余弦定理を使ってみます
ただし,どの三角形のどの部分に余弦定理を使うかによって計算量は大きく変わります。
ここでは△PBQで2通りの式を使って解いてみたいと思います

先ほどとは違う形のyの表示が出てきましたが,
最初の解法で求めたyの式の分母を有理化をしたらこの形が出てきます。
しかしまぁ,最初にこの有理化を施した式を求めてしまった場合,
正解なのかどうか不安で堪らないでしょうね
しかもこれを微分して増減を調べなきゃいけないわけですから
(1)でうっかり計算を間違えてると取り返しのつかないことになりそうです
 平行線と線分の比の関係を用いるパターン
平行線と線分の比の関係を用いるパターン
次は三角比など用いずに中学数学程度の図形の知識で解いてみましょう~
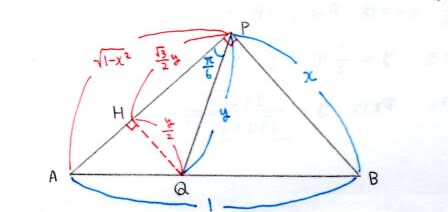
図のように垂線QHを引くと,∠QPH=π/6であるおかげでQHやPHなどの長さが
すぐに分かります。更にQH//PBなのでAH:AP=QH:PBの関係式を用いて立式できます

 ∠Pを円周角とする弧を引くパターン
∠Pを円周角とする弧を引くパターン
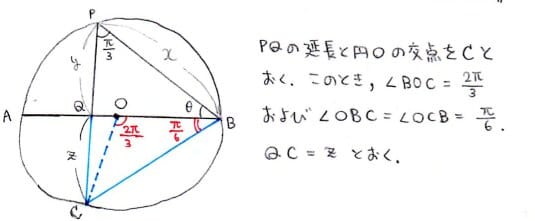
問題文中で円周のことをCと定義していたので上の図で頂点をCとおくのは
ホントはまずかったですね
Pがどの位置にあっても上図の点Cの位置はいつも一緒です。
まずはz,PCの値を求めて,y=PC-zを計算すればOKです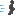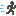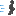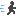


 △OPBが二等辺三角形であることを利用するパターン
△OPBが二等辺三角形であることを利用するパターン
OB=OP=1/2(円の半径)ですので,△OPBはOB=OPの二等辺三角形です
Pが円周上にあるという条件を,この二等辺三角形の条件に置き換えて問題を解くことができます~
さて,∠Bがπ/4より大きいか小さいか等しいかで図がちょっと変わりますので注意しましょう。
特に等しい場合なんかはうっかり忘れやすいので注意です
自分はうっかり忘れてしまいました


(ウ)OB=QBのとき
△OBPは正三角形で,y=PQ=OP=1/2,x=1/2なので
上式はこのときも正しい
ていうのをしっかり添えてやってください
 座標を用いるパターン
座標を用いるパターン
最後に円の中心を原点として座標を入れてXY平面上で考えてみます

まずはPの座標を求めます。直線BPと円の交点の1つが(1/2,0)であることを使うと
多少因数分解が楽になります
Pの座標を求めたら直線PQの式を求めます。傾きはtan∠PQBで与えられます~
∠PQBが直角になるθ=π/6の場合は後で別個に考えましょう

P,Qの座標が分かったのでPQの長さが計算できます

mとxの関係式を求めてyをxの式で表せばOKです~
m<0であることには注意です~

最後にθ=π/6の場合に触れて終了です~

しかしまぁ,結構な計算量でした
 面積を利用するパターン
面積を利用するパターン
△PAB=△PQA+△PQBの関係式から
1/2・x・√(1-x^2)=1/2・√(1-x^2)・y・sin(π/6)+1/2・y・x・sin(π/3)
と立式することもできます
これはなかなか簡単でいいですね
次回は(2)をやっていきます
今回は今年の東北大入試理系数学の第5問をやっていきます~


問題はこちら



まぁ早い話が上の図において,(1)yをxの式で表せ (2)yが最大のときのxは?
という問題です

図形的な問題なので様々な解法があるでしょう。
後半は微分です

今年の東大入試第1問に似た雰囲気があります

yをxの式で表すよう指示しておきながら,xの関数と思って微分するより
角度を変数として微分するほうが簡単といういやらしさがあります~

それではやっていきましょう~

 △PBQで正弦定理を使うパターン
△PBQで正弦定理を使うパターンまずは一番手っ取り早そうな解法からいきます~

△PBQは2辺の長さがx,yになってるので,なんか正弦定理とか使うとうまくいきそうですね

円の中心をO,∠PBQ=θ(0<θ<π/2)とおいておきます。
ABは円の直径なので∠APBは直角です。△APBに着目するとx=cosθであることが分かります

0<θ<π/2 なので sinθ>0 ですから,sinθ=√(1-x^2)です。
これでxとθを結ぶ関係が得られましたね



答えの式がなかなか複雑です

どこまで計算して“答え”とするかは悩みどころですが,
(2)を見れば分かるようにyが最大のときのxを求めるのがこの問題の趣旨のようなので
(1)に関しては答えの形に関してはあまり気にしなくてもよさそうです

ただ,yをどのような形で表示するかによって(2)の計算の面倒さなどには影響は与えそうです。
 △PBQで余弦定理を使うパターン
△PBQで余弦定理を使うパターン正弦定理を使う解法があるなら余弦定理を使う解法だってあるだろう~
ってことで今度は余弦定理を使ってみます

ただし,どの三角形のどの部分に余弦定理を使うかによって計算量は大きく変わります。
ここでは△PBQで2通りの式を使って解いてみたいと思います


先ほどとは違う形のyの表示が出てきましたが,
最初の解法で求めたyの式の分母を有理化をしたらこの形が出てきます。
しかしまぁ,最初にこの有理化を施した式を求めてしまった場合,
正解なのかどうか不安で堪らないでしょうね

しかもこれを微分して増減を調べなきゃいけないわけですから
(1)でうっかり計算を間違えてると取り返しのつかないことになりそうです

 平行線と線分の比の関係を用いるパターン
平行線と線分の比の関係を用いるパターン次は三角比など用いずに中学数学程度の図形の知識で解いてみましょう~

図のように垂線QHを引くと,∠QPH=π/6であるおかげでQHやPHなどの長さが
すぐに分かります。更にQH//PBなのでAH:AP=QH:PBの関係式を用いて立式できます


 ∠Pを円周角とする弧を引くパターン
∠Pを円周角とする弧を引くパターン
問題文中で円周のことをCと定義していたので上の図で頂点をCとおくのは
ホントはまずかったですね

Pがどの位置にあっても上図の点Cの位置はいつも一緒です。
まずはz,PCの値を求めて,y=PC-zを計算すればOKです


 △OPBが二等辺三角形であることを利用するパターン
△OPBが二等辺三角形であることを利用するパターンOB=OP=1/2(円の半径)ですので,△OPBはOB=OPの二等辺三角形です

Pが円周上にあるという条件を,この二等辺三角形の条件に置き換えて問題を解くことができます~
さて,∠Bがπ/4より大きいか小さいか等しいかで図がちょっと変わりますので注意しましょう。
特に等しい場合なんかはうっかり忘れやすいので注意です

自分はうっかり忘れてしまいました



(ウ)OB=QBのとき
△OBPは正三角形で,y=PQ=OP=1/2,x=1/2なので
上式はこのときも正しい

ていうのをしっかり添えてやってください

 座標を用いるパターン
座標を用いるパターン最後に円の中心を原点として座標を入れてXY平面上で考えてみます


まずはPの座標を求めます。直線BPと円の交点の1つが(1/2,0)であることを使うと
多少因数分解が楽になります

Pの座標を求めたら直線PQの式を求めます。傾きはtan∠PQBで与えられます~
∠PQBが直角になるθ=π/6の場合は後で別個に考えましょう


P,Qの座標が分かったのでPQの長さが計算できます


mとxの関係式を求めてyをxの式で表せばOKです~
m<0であることには注意です~


最後にθ=π/6の場合に触れて終了です~

しかしまぁ,結構な計算量でした

 面積を利用するパターン
面積を利用するパターン△PAB=△PQA+△PQBの関係式から
1/2・x・√(1-x^2)=1/2・√(1-x^2)・y・sin(π/6)+1/2・y・x・sin(π/3)
と立式することもできます

これはなかなか簡単でいいですね
次回は(2)をやっていきます















 だといいですが~
だといいですが~




























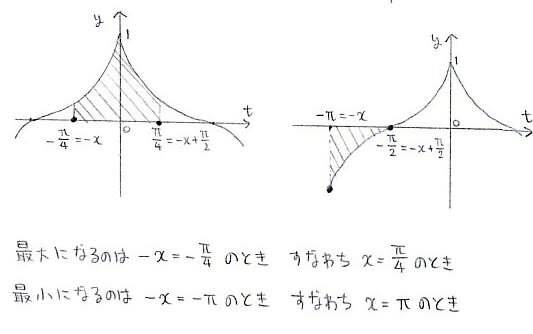





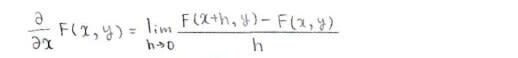





















































 どのkについてa_k=b_kが成り立つか
どのkについてa_k=b_kが成り立つか