2012年東北大入試理系数学第2問その1

どもども。


今回は今年の東北大入試理系数学の第2問をやります～

問題はこちら


1次変換に関する問題です～
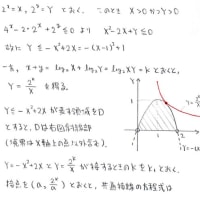
解答の方針がいろいろ考えられるタイプの問題ですが，
ある直線に関して点を対称移動させてその座標を求める，という計算は
恐らく受験までに何度も何度もやらされたことでしょうから
自分に合った方法を既に確立していることでしょう
今回は対称点をいろんな方法で求めてみたいと思いますですよ～

(1)はどのようなやり方でやっても労力はそんなに変わりませんが，
(3)は結構変わってくると思います
行列Bが回転を表す行列だと気付いて利用するかしないかが分かれ目でしょう


まずは(1)です


直線ｙ＝ｘに関して反転させるのがｆ，直線ｙ＝ｍｘに関して反転させるのがｇです。
P(X,Y)をｇによって写した点がP’(s，t)であるとしましょう。
色んな解法パターンを示しますが，いちいち断らないかもしれません。

考え方1
一番基本的な解法からやってみましょ～
・線分PP´の中点が直線ｙ＝ｍｘ上にあること
・直線PP´と直線ｙ＝ｍｘが直交すること
の2点に基づいてs，tに関する連立方程式を立てて解きます






考え方２
ベクトルを使ってみます～
コレ，個人的によく使うやり方です～
ベクトルPP´のことは(→PP´)みたいに書くことにしますね
(→PP´)は直線ｙ＝ｍｘの方向ベクトル(1，m)に垂直なベクトルなので
(→ｄ)＝(-m,1)の定数倍になっています。PP´の中点をMとして，
(→PM)＝ｋ(→ｄ)とおきます。このｋさえ求めれば(→OP´)＝(→OP)＋２ｋ(→ｄ)です





考え方３
もういっちょベクトルでいってみましょ
互いに垂直な1次独立なベクトル(→a)=(1,m)と(→b)=(-m,1)を使って
(→OP)と(→OP´)を表します。そのときの係数を求めましょう





考え方４
直線PP´は点Pを通る傾き(-1/m)の直線です。これとｙ＝ｍｘの交点Mの座標を
求めてそれが線分PP´の中点であることからP´の座標を求めます





考え方５
2点P，P´が与えられたとき，線分PP´の垂直二等分線の方程式を求めることが出来ますが
今回これがｙ＝ｍｘと一致するので，それを使って立式します





考え方６
線分PP´の中点をM，∠POM=∠P´OM=θとおくと，点P´は点Pを原点を中心として
角度２θまたは－２θの回転移動を施したものになっています
２θになるか－２θになるかはPの位置，ｍの正負によって変わってくるので場合分けが必要になってきます。
ただし向き付きの角を考えると，常に２θとおくことも出来そうです
また，θを鋭角のほうに取るか鈍角のほうに取るかによってもcosθ，sinθの符号が変わってきます。
ここでは鋭角のほうを取ってみます。




めんどくさいので最後は割愛してしまいましたが
なるべくならこういうめんどくさい解法は取らないほうがよさげです



考え方７
回転といえば複素数
そんなわけで複素数計算を使ってみましょう～



あとは上の解法みたいに２倍角のcosとsinを求めて代入すればOKです。
向き付きの角を考えてるし，鋭角鈍角の区別もいらないので場合分けなく出来てます





そんなこんなで幾つかの解法方針を挙げましたが，他にもまだまだ色々あるかと思われます
相似を使ってみるとか三平方の定理を使ってみるとか。
またいくつかの解法パターンの合体版みたいのも考えられるでしょうね


続いては(２)です
といっても（２）は一瞬で終わるサービス問題です～

ｇとｆの合成を表す行列Bを求めよっていう問題です
ｆは直線ｙ＝ｘに関する対称移動をする変換ですから
（１）で求めたｙ＝ｍｘに関する対称移動で特にｍ＝１としたものです。
だからｆに対応する行列Cはすぐ求まります
ｇとｆの合成は行列の積ACを計算すればよかです～



なお，ｆは（X,Y）を（Y,X）に写す変換だから～っていう観点からもCを求められます



あとは(１)と同様に多彩な方法でCを求めることが出来ます～
特に４５°の角を活かして求めることも出来そうですね


さて，答えのBの形をよくみると～～。
コレ，回転行列になってます
m=tan(θ/2)とおくと，cosθ＝(1-m^2)/(1+m^2)，sinθ＝2m/(1+m^2)
と書けるので，置換積分するときなど，よくこの変数変換を用いますが，
おかげでこの行列Bに出てくる成分の数値にピンとくる人も多いはずです

今回は　cosφ＝2m/(1+m^2)，sinφ＝(m^2-1)/(1+m^2)　とおけば
回転角φの回転行列になってる事に気付きます

これは今回が特別なわけではなく，直線に関する対称移動を２回施すと
回転移動になるようです
（直線に関する対称移動も上の考え方6，7でみたように原点中心の回転移動を
表していましたが，その回転角は点Pの位置に依存していました。）

試しに１つの図を使ってみてみましょう。


∠POQはαには依存してないですね
これ以外の図の場合も考えてみてください

Bが回転行列だと気付けば（３）は比較的楽に解けるはず。
それはとりあえず次回やりませう～～