
図を見てください。
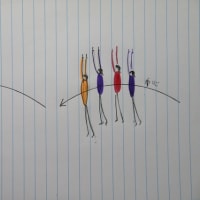
今度は、床の上に立った選手が青い●の位置からボールをやや上方に投げ上げます。ボールが描く放物線の頂点は●で、床に落下した個所は●で表示しておりますが、
ボールをA→B→Cという具合に遠くへ投げた場合と、A→D→Eと近くに投げた場合に、頂点であるBとDの高さが同じである場合、要した時間はどうなんだろう?
ということなのですが、どうでしょうか。
実は、この場合の時間も飛距離に関係なく同じなのですね。
ただ、注意しなければならないのは、横向きのスピードは違いますからね。たとえば前回の記事の問題を参考に考えると、同じ時間(1秒間)に方や20m飛び(つまり、秒速20mですね。)、方や4mしか飛ばなかった(秒速4mですね。)ということになりますと、20m÷4m=5倍。
5倍もスピードが違うってことになるのですね。
この不思議なボールの運動法則がサーブやトスの中に現れるのですが、このことを理解しておくと、戦術を練る上で便がいいのですね。
明日は、時間を算出するための式を紹介し、あさってには、実際のボールの運動と見かけのボールの運動が異なるという話へ進めていきます。(ここ、テストにでますからね。)
では、またよろしくお願いします。












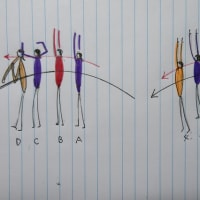


※コメント投稿者のブログIDはブログ作成者のみに通知されます