台形と円の不思議な関係 その２！

全国学力テストが実施され、その問題と解答が新聞に掲載されました。

この問題に立ち向かう子供達を見守る大人達は、

同じ問題にはチャレンジしないでしょうね～

難しくてできない！という場合が多いかと思います。

事実、むつかしいのです。

大人ができなければ面目が立たない！・・・でも

自分ができない難問に立ち向かう子供達を、

なかなかほめようとはしない～

点数は横においといて、まずできた問題があれば、

ほめてあげましょうよ！

 

前置きはこのへんにして

前回の答え

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

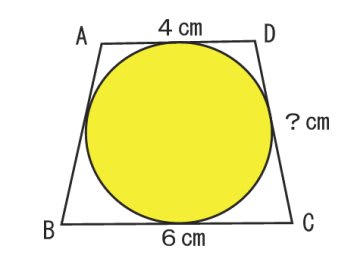
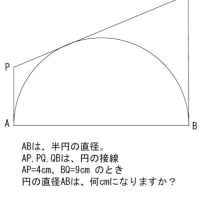
台形の中に入る円があって、辺DCの長さはいくらか？って問題でしたね。

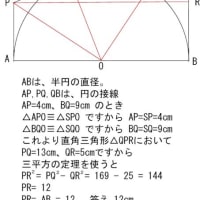
この図に点と線を書き加えますと

直角三角形PODと直角三角形RODは、２組の辺の長さが等しいので

同じ三角形 合同 です。

このことから辺PD＝辺RD＝２ｃｍ

同じように直角三角形QOC＝直角三角形ROCより

辺QC=辺RC＝３ｃｍ

辺DC＝DR+RC＝２＋３＝５   答え ５ｃｍ     

１つの図形の中に、円がぴったり入ると言うことは

図形の辺が円の接線になります。

２つの接線で作られる２つの直角三角形は、いつも合同！

ここがこの問題のミソです。

 

それでは、円と接線の関係が分かったところで

次のような問題なら、どうやって解けばいいのでしょうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

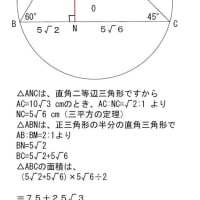
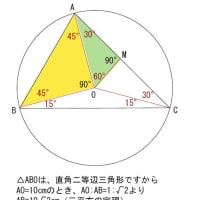
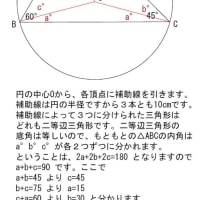
図のように台形に内接する円があり

下底の長さが６ｃｍ、底角が６０°のとき

辺ADと 辺DC の長さはいくらか？

さあ、どうするどうする？