ここで、差分による計算法をつかって、100以上の数の2乗 並びに 100台同士の数の掛け算
を具体的に考えてみます。
方法としては、もちろん、100との差分 をとって考えてます。
先ず、2乗の方から考えます。
例は 124 × 124
差分をとって考えれば、
(100+24+24)×100 + 24×24
= 148×100 + 576
= 15376
となります。4つの四角形で表わしてみましょう。
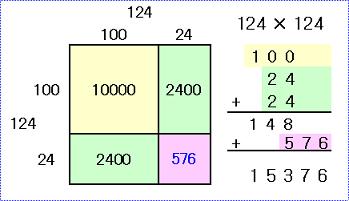
この図でも判ります通り、124 の 2乗 と 24 の 2乗 は下二桁が同じですよね。
先に3つの四角形の合計 (10000+2400+2400) を出したら、あと、576 を足すわけですが、
桁同士がぶつかって実際に足し算をするのは100の位(または1000の位)です。
つまり、148 に 5 を足す計算を考えれば良いわけです。
意外と、簡単でしょう。



さらに、100台同士の数の掛け算一般を考えます。
別に、変わったところはありません。

例は 131 × 123 ですが、
この場合、31 × 23 を 最初に計算しておいた方がいいでしょう。これを先にやって、ちょっと覚えておく。
あとは、131 に 23 を足して 100倍 すなわち 15400 を考えて、覚えておいた 713 を足す。
答えは 16113
あるいは、147 × 168 でしたら
まず、47 × 68 を考えて。。。
7×6 + 4×8 =42+32=74 内側同士と外側同士、それぞれ掛けて足す
74×10=740 それを10倍する
2400+740=3140 それに10の位同士の積を足す
3140+56 = 3196 それに1の位同士の積を足す
3196 これを覚えておいて。。。
147+68 = 215 ⇒ 21500
これに 3196 を 位どりに注意しながら足す
21500
3196
24696 答えは 24696
少し、集中力と注意力が要りますが、やってやれない計算ではありませんね。


この計算法になれるための方法が一つあります。
それは、101×101、102×102、103×103。。。と順に暗算して行くのです。
最初は簡単なんですよ。。。
101×101 = 10201 (10200 + 1)
102×102 = 10404 (10400 + 4)
103×103 = 10609 (10600 + 9)
104×104 = 10816 (10800 + 16)
105×105 = 11025 (11000 + 25)
106×106 = 11236 (11200 + 36)
107×107 = 11449 (11400 + 49)
108×108 = 11664 (11600 + 64)
109×109 = 11881 (11800 + 81)
 楽勝です。
楽勝です。
しかし、だんだん、最後の2乗の足し算のところで100の位への繰り上がりが起きてきます。
最初は1だけですが、
111×111 = 12321 (12200 + 121)
112×112 = 12544 (12400 + 144)
113×113 = 12769 (12600 + 169)
114×114 = 12996 (12800 + 196)
次第に、繰り上がる数も増えます。
115×115 = 13225 (13000 + 225)
116×116 = 13456 (13200 + 256)
117×117 = 13689 (13400 + 289)
118×118 = 13924 (13600 + 324)
119×119 = 14161 (13800 + 361)
120×120 = 14400 (14000 + 400)
121×121 = 14641 (14200 + 441)
。。。。
さらには万の位にも繰り上がり
141×141 = 19881 (18200 + 1681)
142×142 = 20164 (18400 + 1764)
143×143 = 20449 (18600 + 1849)
。。。。
後半、終盤はかなりきつくなりますね。
182×182 = 33124 (26400 + 6724)
183×183 = 33489 (26600 + 6889)
184×184 = 33856 (26800 + 7056)
。。。。
最後はこうなります。
198×198 = 39204 (29600 + 9604)
199×199 = 39601 (29800 + 9801)
200×200 = 40000 (30000 + 10000)
これを自分なりにきつくなるところ、「もういいや」というところまで暗算してみます。
計算方法自体にはなれるでしょう。
私は半分位まで行くとかなり考えるなぁ。。という感じになります。
ただ、曲がりなりとも3桁同士の掛け算を暗算でやるわけですから、
今までやったことのない人でしたら「プチ凄いな」感は得られます。


では、以上を踏まえ、以下の計算を暗算してみて下さい。
(答えは白色文字で書いてあります。色を反転させて確認が出来ます。)
135 × 165 = 22275
142 × 158 = 22436
あっと思った方、この計算法が判った方です。



小学校教育 ブログランキングへ
を具体的に考えてみます。
方法としては、もちろん、100との差分 をとって考えてます。
先ず、2乗の方から考えます。
例は 124 × 124
差分をとって考えれば、
(100+24+24)×100 + 24×24
= 148×100 + 576
= 15376
となります。4つの四角形で表わしてみましょう。

この図でも判ります通り、124 の 2乗 と 24 の 2乗 は下二桁が同じですよね。
先に3つの四角形の合計 (10000+2400+2400) を出したら、あと、576 を足すわけですが、
桁同士がぶつかって実際に足し算をするのは100の位(または1000の位)です。
つまり、148 に 5 を足す計算を考えれば良いわけです。
意外と、簡単でしょう。



さらに、100台同士の数の掛け算一般を考えます。
別に、変わったところはありません。

例は 131 × 123 ですが、
この場合、31 × 23 を 最初に計算しておいた方がいいでしょう。これを先にやって、ちょっと覚えておく。
あとは、131 に 23 を足して 100倍 すなわち 15400 を考えて、覚えておいた 713 を足す。
答えは 16113
あるいは、147 × 168 でしたら
まず、47 × 68 を考えて。。。
7×6 + 4×8 =42+32=74 内側同士と外側同士、それぞれ掛けて足す
74×10=740 それを10倍する
2400+740=3140 それに10の位同士の積を足す
3140+56 = 3196 それに1の位同士の積を足す
3196 これを覚えておいて。。。
147+68 = 215 ⇒ 21500
これに 3196 を 位どりに注意しながら足す
21500
3196
24696 答えは 24696
少し、集中力と注意力が要りますが、やってやれない計算ではありませんね。


この計算法になれるための方法が一つあります。
それは、101×101、102×102、103×103。。。と順に暗算して行くのです。
最初は簡単なんですよ。。。
101×101 = 10201 (10200 + 1)
102×102 = 10404 (10400 + 4)
103×103 = 10609 (10600 + 9)
104×104 = 10816 (10800 + 16)
105×105 = 11025 (11000 + 25)
106×106 = 11236 (11200 + 36)
107×107 = 11449 (11400 + 49)
108×108 = 11664 (11600 + 64)
109×109 = 11881 (11800 + 81)
 楽勝です。
楽勝です。しかし、だんだん、最後の2乗の足し算のところで100の位への繰り上がりが起きてきます。
最初は1だけですが、
111×111 = 12321 (12200 + 121)
112×112 = 12544 (12400 + 144)
113×113 = 12769 (12600 + 169)
114×114 = 12996 (12800 + 196)
次第に、繰り上がる数も増えます。
115×115 = 13225 (13000 + 225)
116×116 = 13456 (13200 + 256)
117×117 = 13689 (13400 + 289)
118×118 = 13924 (13600 + 324)
119×119 = 14161 (13800 + 361)
120×120 = 14400 (14000 + 400)
121×121 = 14641 (14200 + 441)
。。。。
さらには万の位にも繰り上がり
141×141 = 19881 (18200 + 1681)
142×142 = 20164 (18400 + 1764)
143×143 = 20449 (18600 + 1849)
。。。。
後半、終盤はかなりきつくなりますね。

182×182 = 33124 (26400 + 6724)
183×183 = 33489 (26600 + 6889)
184×184 = 33856 (26800 + 7056)
。。。。
最後はこうなります。
198×198 = 39204 (29600 + 9604)
199×199 = 39601 (29800 + 9801)
200×200 = 40000 (30000 + 10000)
これを自分なりにきつくなるところ、「もういいや」というところまで暗算してみます。
計算方法自体にはなれるでしょう。
私は半分位まで行くとかなり考えるなぁ。。という感じになります。
ただ、曲がりなりとも3桁同士の掛け算を暗算でやるわけですから、
今までやったことのない人でしたら「プチ凄いな」感は得られます。


では、以上を踏まえ、以下の計算を暗算してみて下さい。
(答えは白色文字で書いてあります。色を反転させて確認が出来ます。)
135 × 165 = 22275
142 × 158 = 22436
あっと思った方、この計算法が判った方です。


小学校教育 ブログランキングへ











 ならば拡散移動砲? 違います。
ならば拡散移動砲? 違います。