比の学習が始まったら注意する点 マスコミの基準はわれら日本人を大切にしてるか。他国の見方ばかり。

「比の学習が始まったら注意する点」

主な対象は5年生。

ただ、この時期の6年生でも
これからお話しする問題点を抱えているケースが毎年見られます。

4年生以下のお子さんは
そんな問題点がこれから待ち構えているということを
事前に認識しておいてください。

では、いきましょう。

比の学習が進んでいきます

5年生のカリキュラムを見ると
この夏から秋にかけて比の学習が始まる塾が多いんですね。

で、比の学習が始まります。

簡単な整数比に直す方法から始まり
①当たりの大きさ
連比
逆比
と学習が続きます。

そうこうするうちに
これまで学習してきた様々なテーマで
比を用いた新たな解法が登場します。

速さ
平面図形
食塩水
売買損益
仕事算
水量変化
etc.

どれも馴染みのあるテーマです。

そう
この、馴染みのあるテーマだということ
つまり、既に学習が済んでいるテーマだということが
厄介な原因になります。

注意すべき点って何？

ここで先に結論から。

比の学習が始まったら注意する点とは
既習のテーマについて
これまでの解法に固執せず
比を用いた解法を習得する

以前取り組んだ問題とまったく同じものが
これから再登場します。

比を用いて解くことが目的です。

でも、まったく同じ問題なので
以前身に着けた解法でも答えが出せてしまう。

わざわざ新しい解法にしなくても正解しているから
このままでいいや。

そう思ってしまうのも無理はないですね。

また、これまでの解法でたくさんの演習を重ねてきた生徒ほど
その解法に固執します。

これだけ練習したのに。
別の解法とかいらないし。

その気持ちもわかります。

身に着けたものを封印したり手放したりするのは
勇気がいります。

そこの気持ちに折り合いをつけて
比を用いた解法に取り組んでください。

例えば旅人算

ひとつ例を挙げておきます。

＜問題＞

[ ]mはなれたA地点とB地点の間を太郎くんと次郎くんが往復
します。A地点から太郎くんが，B地点から次郎くんが同時に出発
したところ，AB間の真ん中から60mはなれた地点で2人は出会い
ました。太郎くんは毎分55m，次郎くんは毎分45mで進んだとします。
このとき，[ ]にあてはまる数を答えなさい。

旅人算の問題です。

【これまでの解法】
太郎くんの方が速いので、出会った地点は真ん中より60mB地寄りです。

ここで、2人が出会うまでに進んだ距離の差に注目します。
太郎くんはAB間の半分の距離より60m長い
次郎くんはAB間の半分の距離より60m短い
2人の進んだ距離の差は60✕2＝120mです。

2人の進んだ距離の差が120mになるのは出発してから
120÷(55－45)＝12分後

よって、AB間の距離は
(55＋45)✕12＝1200m

【比を用いた解法】
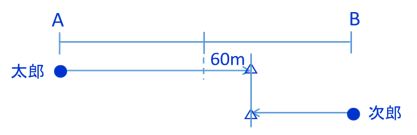
進行の様子を図示すると以下のようになります。

2人が出発してから出会うまでを考えると
時間　同じ
速さ　55m/分：45m/分＝11：9
距離　⑪：⑨

AB間の距離は　⑪＋⑨＝⑳

AB間の半分の距離は　⑳÷2＝⑩

太郎が進んだ距離とAB間の半分の距離との差が60ｍなので
⑪－⑩＝①
①＝60m

よって、AB間の距離は　⑳＝60✕20＝1200m

両方やってみる

いま見てきたように
どちらの解法をとっても正答にたどり着くことができます。

でも、これからの学習で重要なのは
比を用いた解法を身につけること。

比を用いることにより
これまでと比べて処理量を減らすことができます。

あ、でも、これまでの解法も忘れないように。

異なる解法で同じ問題を解くことにより
確かめの計算にもなりますよ。

おしまい。

公約数が見つからないとき 子供が迷ったらお父さんが助ける 家長にまかせろ

 

「公約数が見つからないとき　　どうする？」　　

では、いきましょう。

どうしても見つからない・・・

分数を約分するとき
簡単な整数比で答えるとき

算数の問題を解くにあたり
公約数を探す局面って案外多いんですね。

で、本題です。
公約数がなかなか見つからずに困ることってありませんか？

AとBの公約数を見つけたい
でも、そのAとBがあまりなじみのない整数で、なかなか公約数が見つからない
両方ともわれる数、もうないの？？？

探す手法として
「ユークリッドの互除法（ごじょほう）」
というものがあります。

ご存知の方もいらっしゃるでしょう。
たてAcm、横Bcmの長方形から、切り取ることができる最大の正方形を切り取っていき
最後に切り取った正方形の1辺の長さがAとBの最大公約数になっている
というものですね。

今回はそれ以外の2通りの探し方をお伝えします。

おきまりの　差に注目！

まずは1つ目。

2つの整数の差をとり
その差の約数でわれるか確認してみましょう。

【問題】　209と247の公約数は？

2つの整数の差をとると
247－209＝38

38の約数1・2・19・38
のうち、1以外の2・19・38でわれるか確認します。

2と38は偶数なので、奇数の247と209をわると余りが出てしまいます。

残るは19ですが
209÷19＝11
247÷19＝13

われました。

ということで、209と247の最大公約数は19です。

この手法を用いると
これ以上われる数があるのか、ないのか、が判断できるようになります。

例えば
【問題】　102と107の公約数は？

102は偶数で2でわれるけど
107って・・・われる数あるの？？？

となったとき
2つの整数の差をとってみましょう。

107－102＝5

5ではわれないので、公約数が1以外にないということがわかります。

両方見るから大変なんです

次、2つ目いきましょう。

【問題】　85と391の公約数は？

2つの整数の差が大きい場合には
1つ目の手法は適さないといえます。

そんなときは、われる数がすぐに思いつく方に注目してください。

85は5でわれると、すぐにわかります。
でも、391は5ではわれない。

そこで85を5でわったときの商に注目です。
85＝5×17

391を17でわってみると
391÷17＝23
われました。

ということで、85と391の最大公約数は17です。

なかなか公約数が見つからないときは
この2つの手法のどちらかを試せば
ほぼ解決します。

おしまい。