中学受験での志望校合格を目指す上で、
実際の理科の学習で最も大切なのは「根本原理を理解すること」で
これは間違いありません。
テクニックしか覚えていない人は、
少し違う聞き方をされただけで対応できなくなってしまうからです
しかし、一部の難関校を目指す場合などには、
効率よく問題を処理していかないと時間が足りなくなってしまいま
スピードと正確さ……
一見、相反する二つの要求を満たさなければ、
では、どうすれば 「速く」 「正確に」 解くことができるのか?
その答えは、「根本原理を理解した上でのテクニック」を使うこと
動いている物体が出す音の聞こえ方
まずは、次の例題をご覧ください。
<例題>秒速17mで岸壁に向かって垂直に進む船が、
ただし、音の速さは秒速323mとします。
苦手な人も多い問題だと思います。
この問題を普通に解く場合は、音と船との旅人算になります。
ほとんど算数ですね。
しかも、汽笛は10秒間鳴らし続けていますので、
鳴らし始めた瞬間と、鳴らし終えた瞬間とでは、
この問題を普通に解く場合には、
つまり、上の図のように、3.4km(=3400m)
船と音が出会う旅人算ですから、
3400×2÷(17+323)=20(秒後) に初めて反射音を聞きます。
次に、鳴り終わりの音が出た場所は、
岸壁からは 3400-17×10=3230(m) 離れた位置です。
この鳴り終わりの音も、
3230×2÷(17+323)=19(秒後)
ただし、これは、
汽笛を鳴らし始めてからでいうと、 10+19=29(秒後) です。
つまり、反射音が聞こえるのは、汽笛を鳴らし始めてから20~
29-20=9(秒間) と求まります。
テクニックを使ってみよう!
さて、この問題は計算しやすい数値にしてありましたが、
音の速さを毎秒340mとするような実際の問題では、
そこでテクニックを使ってみましょう。
音の速さが一定なら、
この音波の長さに注目するのが、
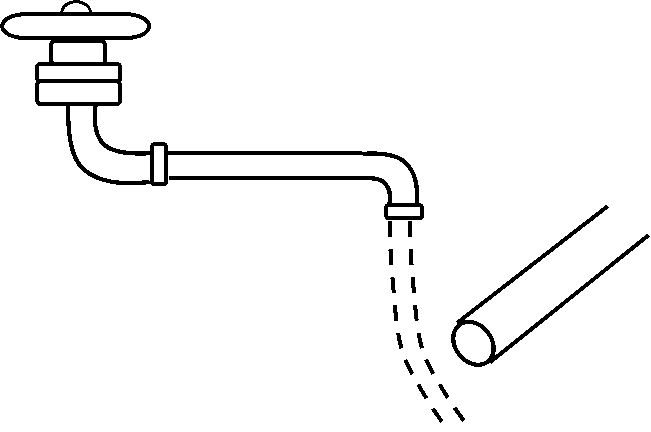
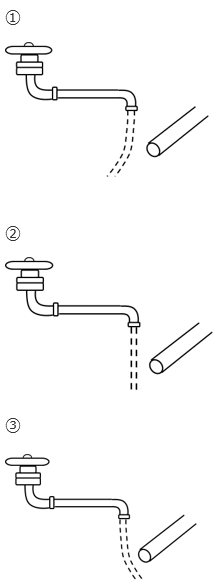
音を出している物体(発音体)や、音を聞いている物体(受音体)
その分だけ音波が縮められて短くなり、音も短く聞こえるのです。
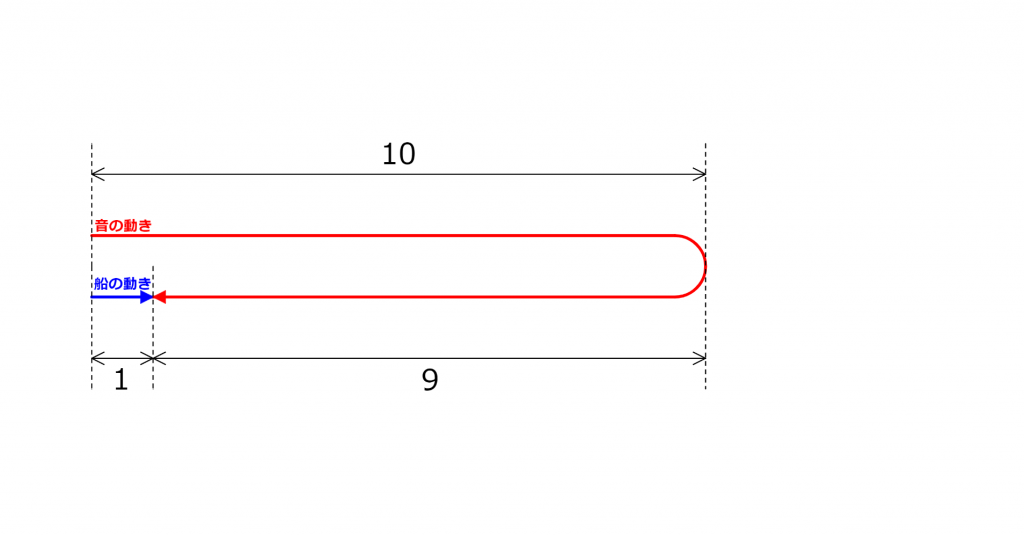
先ほどの「音の旅人算」の図の中から、
今回の問題では、船の速さと音の速さの比は1:
船を出た音が反射して再び船に出会うまでに進んだ距離の比も1:
つまり、比の大きさを数字で書き込むと、このようになります。
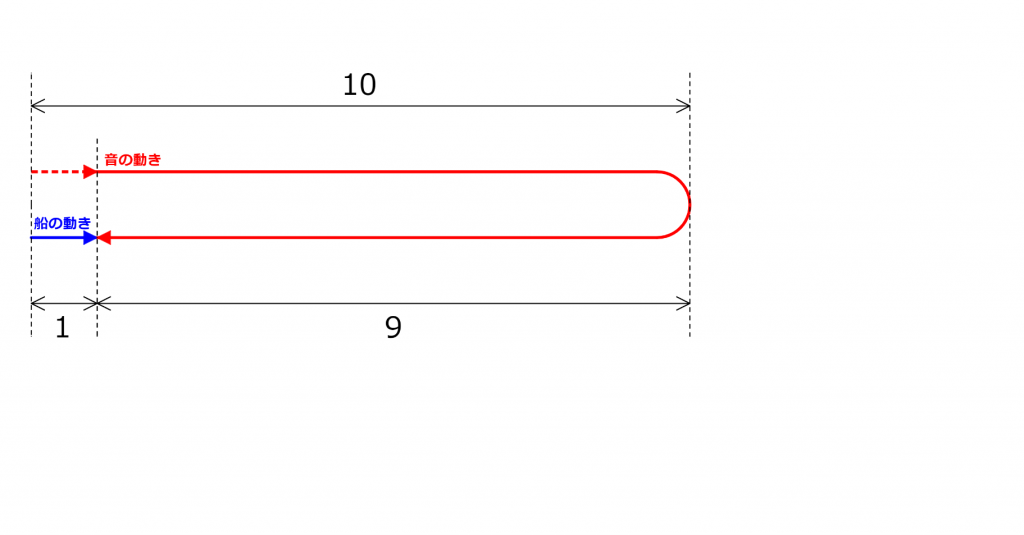
ここで、音を受け取る側だけでなく、
旅人算の状況図としては正しくありませんが、
本来、船が止まっていれば、
船が動くことで、青い部分(聞く側)と赤い点線部分(出す側)
これを、20の中で2にあたる長さ(全体の10分の1)
それに比例して音の長さも短くなるとイメージするのです。
10秒間鳴らした汽笛は、
9秒間だけ聞こえることになります。
コツをつかめば簡単なので、ぜひ試してみてください!












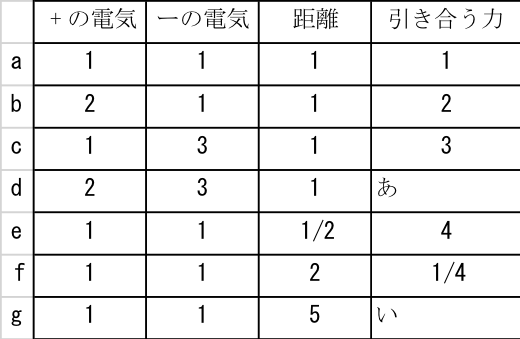
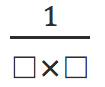 倍になっている
倍になっている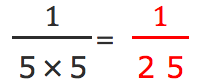

 く
く