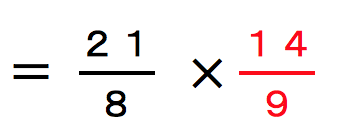表面積は簡単！～立体図形～ がんばろう大日本 令和二年度

令和二年度の入試問題を見ていると、立体に関する問題が以前より

難度が高くなっていることに気づかされます。

 

そこで本日は、立体の問題、特に、表面積の求め方について

まとめたいと思います。

 

表面積を求める問題は、手立てはすぐにみつかるのですが、正答にたどり着くには

時間がかかったり、計算ミスをおこしてしまったりと厄介な問題になります。

しかし、本日は、手順が分かっていれば必ず解ける方法をご提示いたします。

 

それでは実際に問題を解いていきましょう。

 

問題【1】次の立体の表面積を求めなさい。

 

表面積は、基本、

3方向から見てください。

 

上、手前、右の3方向です。

 

 

 

 

 

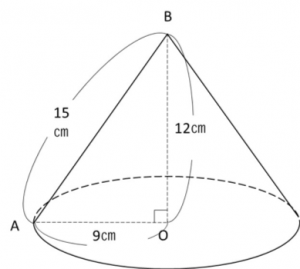
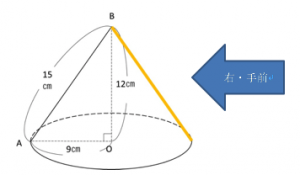
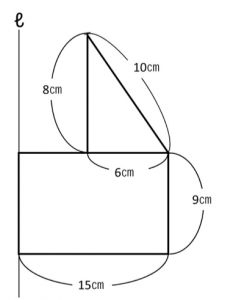
円すいの場合、右からみた表面積と、手前から見た表面積は同じなので、

2方向からで大丈夫です。

 

 

しかし、立体図形は、3方向から考えることを基本と覚えておいてください。

 

まず、「上」からみると

 

円Oが見えますね。

 

次に、「手前」と「右」からみると、

 

 

 

 

 

 

黄色で塗った部分が見えます。

 

この黄色い部分を開くと、おうぎ形になるので、

右図のようなおうぎ形になります。

 
 

円すいの側面のおうぎ形の面積を求めるには、

母線と半径が必要になるので、展開図は、次のように描きます。

 

 

底面の円もくっつけて描くようにしましょう。

 

部分図が描き終わったので、次に式を立てて解いていきます。

 

【式】　9×9×3.14＋15×15×3.14×＝(81＋135)×3.14＝216×3.14＝678.24㎠

 

 

以上です。

 

まとめると、

①3方向(2方向)から見る

②部分図を描く

③式を立てて解く

 

この3ステップです！

これだけで確実に解けるようになります！

 

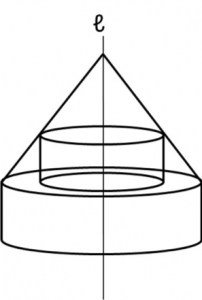
更に、回転体にもチャレンジしてみましょう！

 

 

 

 
 

 

問題【2】右の図のような直角三角形と長方形を

組み合わせた図形を、直線ℓを軸として回転してできる

立体の表面積を求めなさい。

 

 
 
 
 

 

まず、回転した時の完成図を描きます。

 
 

先ほどの3ステップを思い出してください。

まず、ステップ①3方向から見る

上から見ると、半径9㎝の円が見えます。

 

 

 

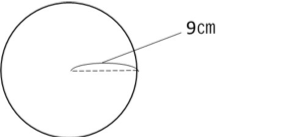
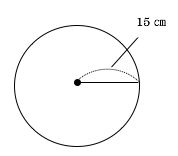
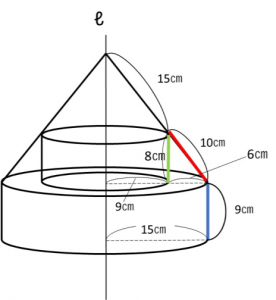
また、下から見ると、半径15㎝の円が見えます。

 
 

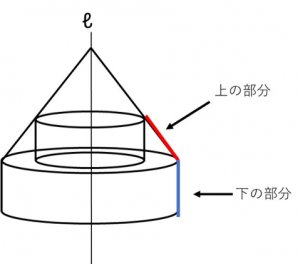
次に、右から見ると、

上の部分と下の部分が見えます。

 

 

上の部分は、円すいの一部となり、下の部分は円柱の側面になります。

まず「上の部分」赤いところの側面積は、

円すいの一部なので、

 

 

 

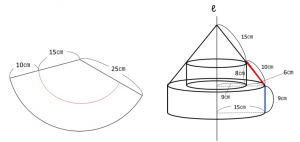
この15㎝、25㎝は相似形を利用して求めています。

 

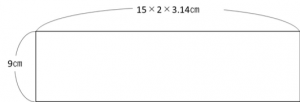
「下の部分」青い部分は、円柱の側面になるので、長方形になります。

 

 

 

 

あと、最後に忘れていけないのは、上から覗き込んだときに、空洞になっている部分の側面です。

 
 
つまり、

 

図の緑の部分です。

 

この部分は、半径9㎝の円柱の側面ということがわかるので、

 

 

 
 
右の図の長方形になります。

 

 

 

これでステップ②部分図を描くところは終わったので、

 

あとは、

ステップ③式を立てていきます。

 

9×9×3.14＋15×15×3.14＋25×25×3.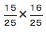14×＋9×15×2×3.14＋8×9×2×3.14

 

＝(81＋225＋240＋270＋144)×3.14

＝960×3.14

＝3014.4㎠

 

 

となります。

最後の式に持っていければアッという間ですが、式が長いですね。

3.14でまとめることも忘れないようにしましょう。

式からもわかるように、この回転体の表面積は、部分が、5か所にわかれています。

これを頭の中だけでやっていくのは、無理です！

「半径」や「高さ」を求めながら、式も作って、部分を考えるということは、

どんなに計算が得意だとしても、どこかで計算ミスをしてしまったり、見落としてしまったりということが起こります。

 

必ず、部分図を描いて式を作ってから解くようにしましょう！

最後は、3，14でまとめるということも忘れずに。

 

本日は、表面積を求めるときの手順3順番でした。

分数計算～手順が大事～ がんばろう大和民族

こんにちは

本日は、「手順」が大事！

 

というお話をしたいと思います。

 

分数計算

 

 

という問題で、（分数のやり方はすでに知っているという前提で話を進めていきます。）

 

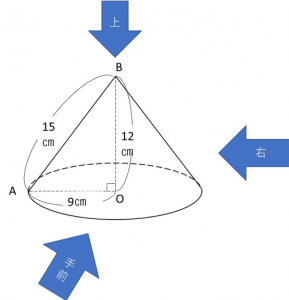
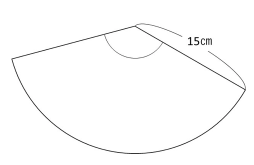
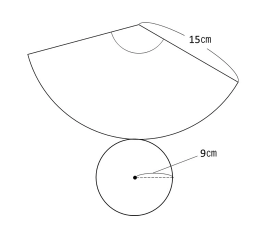
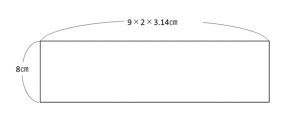
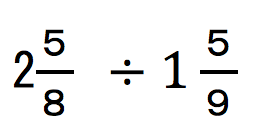
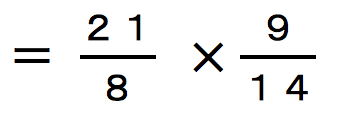←一気にこの状態に持っていく生徒さんが多い

上の式は合っているので、まーまー良しとします。

しかし、この手順でやってしまうと、

 

 

というミスを犯してしまう生徒さんが40％くらいいます。（40％は個人的な感覚です）

5人に2人くらいの割合でミスをする生徒さんが出てきます。

5回計算問題を解いて2回くらいミスをすると考えてもいいかもしれません。

 

つまり、100％の正答率からはかけ離れてしまうということです。

 

とにかく、「リスクを減らす」というのが算数の問題を解く上で大事な心掛けです。

 

「確実性」と「スピード」のどちらを先に選ぶかは、

やはりまずは「確実性」です。「スピード」は確実に解けるようになってから十分

練習はできます。しかし、「確実性」は「スピード」からは生まれません。

 

分数の計算の手順は以下のようになっています。

 

 

①帯分数を仮分数にする

②÷を×にし、×の後ろの分数を逆数にする

③約分する

④仮分数を帯分数にする

 

という4つの手順があります。

これだけの手立てをやっているのです。

頭の中でこれを一気にやるのではなく、

1回につき1作業を守り、ノートに書いて解いていきましょう！

特に逆数にするとき、÷を×に直しただけで終わりにしないようにしましょう。

 

では、分数のたし算・ひき算ではどうでしょうか。

 

 

やはり3つの手順に分けることができます。

①通分する

②帯分数のまま引き算の形をつくる

③整数部分と分数部分に分けて計算

 

分数のたし算・ひき算の解法で指導の中でよく見かけるのが、

 

 

という、初めの段階で、帯分数を仮分数にしてから通分、計算をする方法です。

間違ってはいません。

 

しかし、②のプロセス、通分するために□倍するというところに

リスクが潜んでいます。

大きな数字になればなるほど、計算ミスをしやすくなるのです。

更に、③の引き算、また、④の仮分数をあらためてまた帯分数に直す

というところにもリスクが潜んでいます。

 

計算のモットーは、「リスクを減らす」ということにあります。

 

大きな数字にするまえに、まずは「帯分数のまま」で「通分する」

「かけ算の形にもっていって早めのうちに約分する」など、

リスクを減らす手立てを知っているのであればそれを使うべきです。

 

仮分数に直してから全部を通分するというやり方は間違っていないので

絶対にやってはいけないとは言えませんが、

「リスクを減らす」という観点からもう一度自分の計算方法を見直してみてください。

 

「手順」は、どの問題でも大事です。

 

すっ飛ばして先をやってしまうと、思わぬところでつっかかっているということもあります。

もちろん、慣れてきて、自分は絶対に計算を間違わないと誰もが認めるくらいまできたら、

スピードをつけるために手順をすっ飛ばしてもいいでしょう。ただ、順番は間違わないようにしましょう。

 

 

余談ですが、分数のこの手順は、実はAIには難しいそうです。

AIに難しいことを、人間は、小学3年生、4年生ですでに習得しているのです！

それは、ちゃんと「手順」を踏むということができるからです。

 

人間てすごいね。

日本人すごいね。