マンスリー１カ月対策〜流水算を制する者は速さを制す 大和民族繁栄がんばろう

今回は、５年生の10月マンスリーテストに的を絞ってお話しいたします。

5年生は、これから速さと比、旅人算、流水算、時計算、通過算と速さが続きます。

まず、この「速さ」の単元でつまずく第一のポイントは、
単位変換がまだしっかりと定着していない
という可能性があります。

そういうお子様は、秒速、分速、時速の関係図を書いてあげて、問題を出して確認です。
演習は、SAPIXですと、BASIC「速さ」P.9ステップ①、P.10 ステップ②　P.11 ステップ③
四谷の予習シリーズ５年上「基本演習問題集」１６回速さ（２）P．70トレーニング１
にありますのでしっかりと練習しましょう。

また、次のステップでつまずくお子様は、
速さの三公式がまだ使えていないという状況が考えられます。
速さは、きょりと時間がわかれば出てくる。
つまり、どれだけの時間かかって、どれだけ進んだかを表しているのが「速さ」という
ものなので、問題を読んだ時に、まずは、きょりや時間にチェックを入れましょう。

更に、
「速さ」には、「旅人算」「流水算」「時計算」「通過算」と
入試の出題率から見ても、多様な問題が作られています。

その中で、大きくつまずいてしまうのが「流水算」でしょう。

速さが、上り、下り、流速、静水時の4つ出てくる上に、
更に、流速が変わったり、
こぐ速さを変えたりと、
途中で速さが変わってしまう問題もあります。

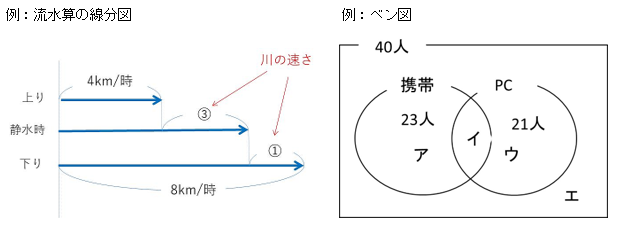
流水の問題では、４つの速さの関係を線分図に表しましょう。
初めのうちは簡単なので、線分図を書かなくてもできると
全く書かずに頭の中だけでやってしまう生徒さんが多いですが、
簡単なものから書いておかないと、少し難しくなっただけで
全く書くことができず解けないということが起こっています。

例えば、
上流のA地点から16㎞下流にあるB地点まで、上りに４時間、下りに２時間かかる
船があります。

上りの速さは、１６÷４＝４km/時
下りの速さは、１６÷２＝８km/時
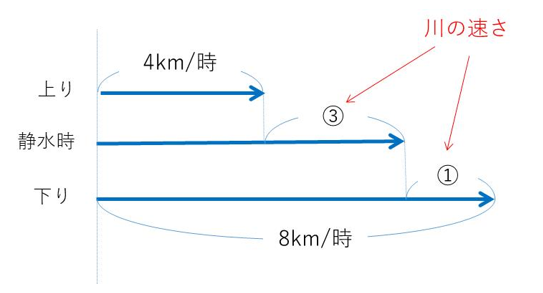
ということがわかったら、すぐに線分図にしてみてください。

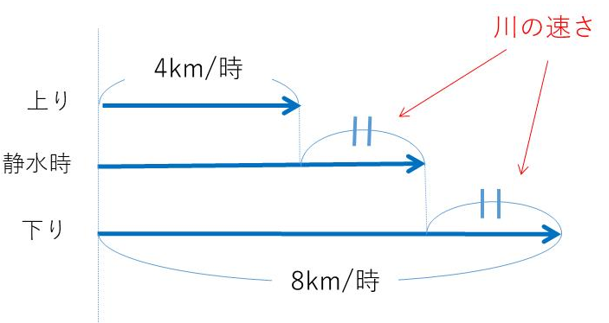
ここから川の速さ、静水時の速さを求めることができます。
流速は、（８−４）÷２＝２km/時

流速が変わる問題は、

上流のA地点から16㎞下流にあるB地点まで、下りに２時間かかりましたが、
帰りは、流速が３倍になっていたため、4時間かかりました。
という問題があるとします。
この時の線分図を書くことができるか試しにやってみてください。

この時の、流速は、
行きは、（８−４）÷④＝１km/時
となりますが、帰りは１×３＝３km/時です。

次に、静水時の速さが変わる問題は、
線分図がやや描きにくいのですが、

例えば、
上流のA地点から14㎞下流にあるB地点まで、上りに7時間かかりましたが、
こぐ速さを２倍にしたので、下りは２時間で着くことができました。
という問題があった場合、

上りの速さは、１４÷７＝２km/時
下りの速さは、１４÷２＝７km/時
です。

上りは、静水時ー川＝２km/時
下りは、静水時×２＋川＝７km/時
上り＋下り＝静水時×１＋静水時×２＝９km/時
川は変わっていないので、
上りと下りの速さの和は、川の速さが消去されて、変える前の静水時と変えた後の静水時となります。

つまり、

上りと下りの和は、変える前の静水時＋変えた後の静水時

静水時が変わる前の線分図を書くと、

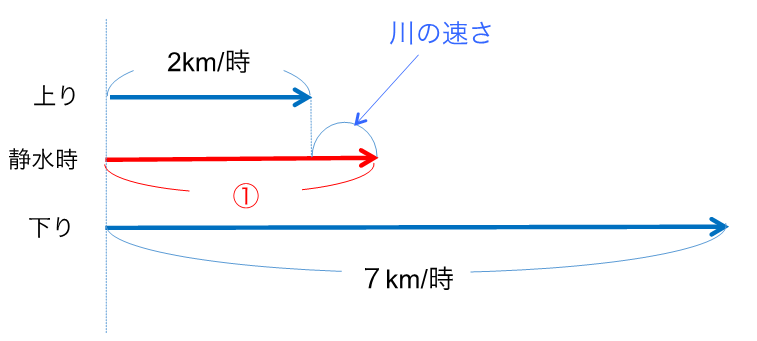
この線分図に変わった後の静水時を書いてしまうと、
ややわかりにくくなるので、

上りと下りの和は、変える前の静水時＋変えた後の静水時

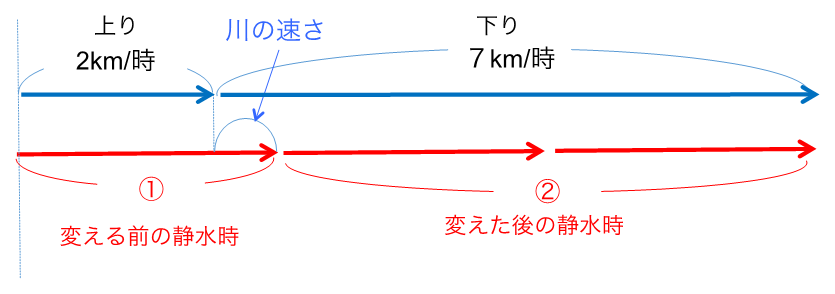
この関係を知っていると便利です。
テストでも使えます

特殊算〜消去と代入法と和差算 強く優しい国なろう大日本帝国

特殊算についてお話しいたします。

特殊算とは、
つるかめ、和差算、過不足算、消去算、差集め算を指します。

その中で消去算は比較的得意だが、代入法になると意外と
間違えてしまったりという生徒さんも多いのではないでしょうか。

そこで、今日は、代入法の簡単な解き方をご紹介いたします。

例えば、
「モンブランケーキ３個と抹茶アイス２個で1600円です。
モンブランケーキは抹茶アイスより150円高い。
モンブランケーキはいくらでしょう」

という問題があるとします。

モ×３＋抹茶×２＝１６００
モ＝抹茶＋１５０

とまず式を書くことは皆さんできますね。

次に、塾やテキストなどで教えるスタイルは、
この「モ＝抹茶＋１５０」を
モ×３＋抹茶×２＝１６００

の式の、モ×３の所に代入するという方法です。

これが、意外と子どもたちの思考では難しいものなのです。

そこで考えたのが、
和差算の投入です！
線分図で
モンブランケーキと抹茶アイスを表してみます。

和差算の方法で、
モンブランケーキの高い150円を３つ分１６００円から引くと、
１６００—１５０×３＝１１５０
１１５０が抹茶アイス５個分になるので、
１１５０÷５＝２３０円・・・これが抹茶アイス１個分の値段です。

そうすると、モンブランケーキは、２３０＋１５０＝３８０円
となります。
大人の思考では、
代入法はすんなり「入れ替える」という概念があるので
しっくりくると思いますが、
子どもたちの思考では、
まだ方程式もないので、
代入する→「置き換えて入れ替える」という思考がなかなか難度の上がる技になります。

この和差算方式を利用すれば、
「モンブランケーキは、抹茶アイスの２倍よりも３０円高い」という
問題になっても簡単に解くことができます。

問題
「モンブランケーキ３個と抹茶アイス２個で1290円です。
モンブランケーキは抹茶アイスの２倍より30円高い。
モンブランケーキはいくらでしょう」

結局、
１２９０から余分の３０円３つ分を引いて１２９０−３０×３＝１２００
この１２００円が、抹茶アイス②×３＋①×２＝⑧となるので、
１２００÷⑧＝１５０円・・・これが抹茶アイス１個分の値段となります。

モンブランケーキは、１５０×２＋３０＝３３０円です。

いかがでしょうか。

算数を教えてていつも思うのが、
式や解法だけではなく、問題を目で見えるようにしてあげることこそが
算数を指導する醍醐味ではないかと思うのです。

式でぱぱっと解くことはできますが、
どうしてそうなるのかを「目で見えるように」「イメージ化」することが大事です。
算数の問題をいかに「イメージ化」できるかを
日々研究して指導していきます。

 

問題を解くカギ〜イメージ図とイメージ式 がんばろう日本人大和民族

教えている方としては、
テストの時に何を思い出して欲しいか。
問題を読んだ時に何を思い浮かべて欲しいか。

結論から申しますと、

算数の問題を読んだとき、
イメージ＝解けるイメージ＝解くための図式＝解くポイント

これを浮かべて欲しいのです。

「言われた通りにイメージ図を描く」
ときには、図ではない時もあります。その時は、
「言われた通り式にする」

これが大事です。

勝手な想像で、思い込みで解かない

この時期の6年生だと、いろいろな問題に当たっていて
余計に考え過ぎてしまうということが起こります。

むしろ習いたての5年生の方ができてしまうということも

そのままシンプルに考える

ということができなくなってしまっているのです。

例えば、

「写真の現像を頼むとき、50枚までは1枚ア円に手数料100円がかかります。
51枚以上では、1枚イ円で現像できます。
34枚現像するのと55枚では料金が一緒で、また、50枚と75枚でも料金が一緒になります。
アとイに当てはまる数値を入れなさい」

という問題があったとします。

とにかく、言われた通りに式にするしか手立ては無さそうです。

強いて言うなら、
やはり○○が一緒という言葉から、比が連想できればなおいいのですが。
皆さんはどうでしたか。

では式にしてみます。

50枚までは手数料が100円かかるので、
34×ア＋100円

また、55枚だと51枚以上になっているので、
55×イ

ということより、この2つが等しいので
34×ア＋100円＝55×イ・・・・①
もう一つの文章から、
50×ア＋100円＝75×イ・・・・②

① ②の式より、
100円が消去できるので、

② －①
16×ア＝20×イ

この式は！！
比の利用ができますね。
この部分で、式は作ったはいいけど、その先が。。。という生徒さんも
無きにしも非ず。

等しいときたら比から逆比の利用ができる

ということも頭に入れておいてほしいポイントです。

ア：イ＝⑤：④
ということより、
⑤×34＋100＝④×55
[170]＋100円＝[220]
[50]＝100円

① ＝2円
となり、ア＝⑤＝10円、イ＝④＝8円

となります。

いわゆる上位校となると、
一旦式に表して比の①を求めるという問題が出題されます。
文章で言われていることを式にするというのは、中学で学ぶ方程式に通じるものだからでしょう。

言われた通り、とにかく、式にしてみるというのもとても大事です。
ただ、問題をじーっと見ていても解けません。
よく、
「手を動かす！」

と先生から言われることがあると思いますが、
なんでもいいからとにかく書いてみるということです。

思い込みや、習った式に当てはめようとするのではなく、
書いてみてから考えるということも大事です。

いろいろと想像力を膨らますことも大事だと思います。

「なんと（７１０）きれいな平城京」

という語呂合わせがありますが、それを聞いて、
ぱーっと目の前に、平城京の様子を頭に浮かべるとか、

「1192（いいくに）作ろう鎌倉幕府」と聞いて
武士がうぉーっと刀を上げているシーンとか

それぞれ、言葉をきいて想像を膨らまして
そのイメージを頭に入れるというのはとても楽しいことでもありますよね。
算数も、イメージ図やイメージの式をパッと浮かぶようにできたらいいなと
思っています。

 

数と規則性 毎日労働家族のための家長のお父さま 大和民族

本日は、数と規則性についてお話いたします。

数列にはいろいろなルールや規則性があり、自分で発見できると楽しいものです。

例えば、
１，１，２，３，５，８，１３，２１,　３４・・・・・・
などは、よくご存じのフィボナッチ数列

簡単に言うと、
「直前の2項を足した数を並べていく」
という規則性ですよね。

1+1＝2
1+2＝3
2+3＝5
3+5＝8
・・・・

と。

また、前前項÷前項を計算すると、

1÷1＝1
1÷2＝1/2＝0.5
2÷3＝2/3＝0.66666…
3÷5＝3/5＝0.6
5÷8＝5/8＝0.625
8÷13＝8/13＝0.615…
13÷21＝13/21＝0.619…
というように前々項÷前項＝黄金数-1に近づいていくということがわかっています。
黄金比というのは、
人間が心地よい、美しいと感じる比率と言われています。
デザインなどでよく用いられています。

黄金数は、

黄金比率は、

長方形のたて対横の比が、
だいたい1：1.6＝5：8（5÷8＝0.625）が、しっくりくる大きさになっています。

更に、
前項÷前前項にしてみると、
1÷1＝1
2÷1＝2
3÷2＝1.5
5÷3＝1.666666…
8÷5＝1.6
13÷8＝1.625
21÷13＝1.615384615…
34÷21＝1.619047619…
というように、1.6180339887…の黄金数に近づいていきます。

規則的に並んでいる数字に何か規則がないかな？という思いで見てみると、
問題ももっと楽しく解けるはず？？

また
数字の特徴を生かすと、
4×4×4　×　4×4×4　×　4×4×4

という問題が出たとしても、

「4×4×4＝8×8」
4＝2×2
4×4×4＝2×2　×　2×2　×　2×2
＝2×2×2　×　2×2×2
＝8×8

ということに気付けば、8×8＝64なので、64×64×64をするだけで済みます。
4を9回かけるよりも少し速いのではないでしょうか。

更に、
三角数を皆さんご存知だと思いますが、
奇数の数が並ぶ三角数を考えてみたいと思います。

各段の和に何か規則性はないでしょうか？

実は、
1＝1×1×1
8＝2×2×2
27＝3×3×3
64＝4×4×4

ということが分かれば、10段目に並んだ数字の和？と聞かれても、
わざわざ10段目の一番左や右を求めなくても、
10×10×10＝1000と出すことができます。

では、
偶数になったらどうでしょうか？

各段の和に何か規則性はないでしょうか。
ヒントは、先ほどの奇数を参考にしてみてください。

2＝1×1×1＋1
10＝2×2×2＋2
30＝3×3×3＋3
68＝4×4×4＋4

というように、奇数の各段の和にそれぞれの段数を足すと求められます。

このように、
数には何かルールが隠されているのではないかと考えてみると、
計算が楽になったり、
視点を変えてみることができるようになり、
考え方が広がる→思考力がつくということになります。

各学校の入試問題も、根本原理をうまく誘導して
問題に盛り込んでいることが多いです。

算数の答案作成力 頑張ろう大和民族みんな

「記述力とは何か」

式、図、表、言葉

この4つをしっかりと普段から書けるようにしましょう。
いきなりテスト本番で書けるようになるということはないので、普段の授業から
自分の考えたプロセスを残すようにしましょう。

１．式
算数の問題は、必ず式があります。
テストが終わった後に、テストの問題用紙を持ってきてもらうのですが、
問題の横に書きなぐった筆算や、ごちゃごちゃっと書いた数字などが残っていることがあります。
もちろん、それでもいいのですが、ちゃんと式を書いて解くようにしましょう。
特に後ろの方になる大問は、１つ１つ式を書くことによって、自分の頭の中を整理するということにもなります。ただ、ただ、問題の字ずらを追って、
見えた数字だけを式にするのではなく、考えた後を残すという意味で式を書いてほしいのです。

2．図
図には、線分図、面積図、ベン図、進行図、てんびん図・・・などがあります。
どの問題でどう使うのかは練習が必要です。
また、図の目的は、問題を整理してわかりやすくするということでもあります。

3．表
規則性や場合の数は「表」にして整理するという手段があります。
とにかく手を動かして、自分で書き出すということが大事であり、書いているときに
気づけるようにするということです。

4．言葉
2×3＝6という式だけでもいろんな意味があります。
「2個ずつ3人に配った」のか、「比の②が3倍」されているのか。

また、6という答えも「女子の人数」を求めたのか「行きの速さ」を求めたのか、
などなど、答えにもいろんな意味があります。
この時に、しっかりと自分で「何を求めたのか」ということを意識することが大事です。

この4つ、「式、図、表、言葉」を書けるようにするというのは、集団授業での指導ではなかなか難しいものがありました。
そのまま、真似して書いてほしいのですが、問題集などは、完成した図しか書かれていないので、
どうやって書くのか、どこから書くのかということが、指導しにくいものがあります。

書き順があるのです。
「○かいて、チョン、○かいて、チョンだよ」と
よく生徒に言っています。

順番を間違えて書かないように。
図を描く順番まで教えることができるのは、
個別のメリットでもあります。

普段からどうやって図を有効に使うのか、
それを示していきたいと思います。

テストでは、自分を落ち着かせるためにも、
しっかりと図や式を書くようにしましょう。