どもども。
前回は今年の京大入試理系数学の第3問をやりました~
今回は別の手法でこの問題を考えてみます
前回:http://blog.goo.ne.jp/mathnegi/e/2b66ed8cc2a052c6ff52a4c29b1988f6
問題:http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon3.html
前回は,X=x+y,Y=xy という変数変換を使いましたが,
今回はまずは線形変換を使ってみましょう。
x^2+xy+y^2=6 が表す楕円を短軸と長軸がx軸,y軸となるように
すなわち AX^2+BY^2=C の形になるようにX,Yをとってみたいと思います。
x^2+xy+y^2 という式はいわゆる2次形式と呼ばれてるもので,
対称行列(元の行列とその転置行列が等しい行列)を使って行列の積表示に直すことができます。
ここに現われる対称行列の対角化を利用して欲しい変換を手に入れます

とまぁ,固有値と固有ベクトルを求めますです。
固有ベクトルは絶対値が1になるように正規化したものを使います。
何やらcos45°,sin45°を匂わすような√2とか出てきますね

ここで出てきたTは直交行列と呼ばれます。転置をとると元の行列の逆行列になっています。
正規化するのは実はTを直交行列にするためだったり。
そーいうコトを大学の線形代数で学びますよ~。
そもそも x^2+xy+y^2 はx,yの対称式でした。
一般にy=f(x)のグラフと逆関数x=f(y)のグラフは直線y=xに関して対称になっていますが,
そのことからx,yに関して対称な関数(あるいは曲線)というのは直線y=xに関して
線対称になっていることが分かるかと思います。 x^2+xy+y^2=6 もまさにそれで,
短軸と長軸が直線 y=x,y=-x になっています。先ほど45°ぽい数字が出てきたのはそういうことだったんですね。
なのでそれを意識すればわざわざ固有値の計算とかしなくても上手い変数変換を見つけられたりするわけですね。
√2 なしで X=x-y,Y=x+y とおいた方が,この後の計算が実は楽になったりもするかも
さて,手に入れた新変数を使って解析を進めます。

x^2y+xy^2-x^2-2xy-y^2+x+y=k をX,Yの式で表します。
X^2=の形に直すと少し扱いやすそうなYの関数が得られました。
どちらかというとXとYが逆の方が見栄えがイイデスネ
ついでにXに付いた2乗が邪魔です。
というわけでX^2=y,Y=xという風に更に置き直してしまいました。
Xに付いた2乗を無くしたおかげで楕円が2次関数になっちゃいましたよ
X^2=yとおいたので,y≧0の部分のみを考えなければならないことに注意です。
f(x)=(x-√2)^2-(√2/x)k は,放物線 y=(x-√2)^2 と双曲線 y=(√2/x)k
の各xに対するy座標の差として考えることができますね。
y≧0で考えるので,放物線の方が大きい部分を考えなければなりません。
これでイメージを膨らましながらy=f(x)のグラフを考えてみましょう。
k>0,k=0,k<0の場合に分けて考察します。
まずはk>0の場合を考えますが,放物線 y=(x-√2)^2 と双曲線 y=(√2/x)k は
必ず交点を持つことが分かります
交点のx座標がy=f(x)の零点になるわけですね。
kが大きい時は交点が1個ですが,小さくなると複数になります。
とりあえずy=f(x)のグラフをx>0部分とx<0とに分けて考えて
それぞれが放物線 y=-3x^2+12 と交点を持つようなkの範囲を求めます




続いて,放物線と双曲線が交点を複数持つ場合です。
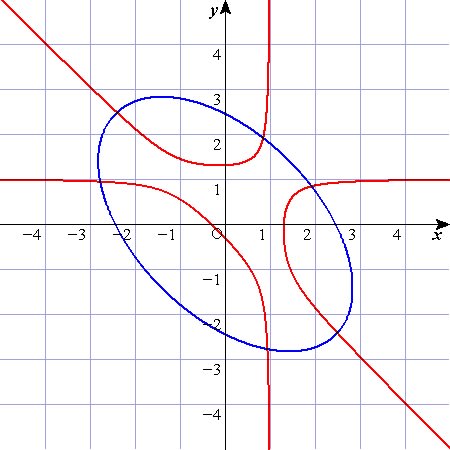
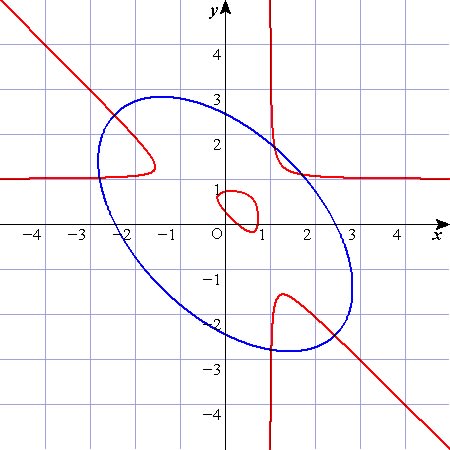
前回,元の変数のままでkを動かしてグラフの変化を見てみましたが
途中で真ん中に変な島みたいなのが出現しましたよね。
それに相当する部分ですかね,この交点が複数現われて来る現象は~。

kを0に近づけていくとどんどんαは√2に近付いていきます。
だから相変わらずy=f(x)のグラフは放物線 y=-3x^2+12 と交わるんですね。
k=0の時も問題ありません。
k<0の場合もまったく同様に考えます。

というわけでy=f(x)のグラフが放物線 y=-3x^2+12 と交点を持つような
kの範囲を求めることができました

やはり骨が折れますね


試験場でこんな大層なことをやることはまず不可能でしょう
次回はメンドクサイ解法をもう1パターンやってみます(まだやるんかーい )
)
前回は今年の京大入試理系数学の第3問をやりました~
今回は別の手法でこの問題を考えてみます

前回:http://blog.goo.ne.jp/mathnegi/e/2b66ed8cc2a052c6ff52a4c29b1988f6
問題:http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon3.html
前回は,X=x+y,Y=xy という変数変換を使いましたが,
今回はまずは線形変換を使ってみましょう。
x^2+xy+y^2=6 が表す楕円を短軸と長軸がx軸,y軸となるように
すなわち AX^2+BY^2=C の形になるようにX,Yをとってみたいと思います。
x^2+xy+y^2 という式はいわゆる2次形式と呼ばれてるもので,
対称行列(元の行列とその転置行列が等しい行列)を使って行列の積表示に直すことができます。
ここに現われる対称行列の対角化を利用して欲しい変換を手に入れます


とまぁ,固有値と固有ベクトルを求めますです。
固有ベクトルは絶対値が1になるように正規化したものを使います。
何やらcos45°,sin45°を匂わすような√2とか出てきますね


ここで出てきたTは直交行列と呼ばれます。転置をとると元の行列の逆行列になっています。
正規化するのは実はTを直交行列にするためだったり。
そーいうコトを大学の線形代数で学びますよ~。
そもそも x^2+xy+y^2 はx,yの対称式でした。
一般にy=f(x)のグラフと逆関数x=f(y)のグラフは直線y=xに関して対称になっていますが,
そのことからx,yに関して対称な関数(あるいは曲線)というのは直線y=xに関して
線対称になっていることが分かるかと思います。 x^2+xy+y^2=6 もまさにそれで,
短軸と長軸が直線 y=x,y=-x になっています。先ほど45°ぽい数字が出てきたのはそういうことだったんですね。
なのでそれを意識すればわざわざ固有値の計算とかしなくても上手い変数変換を見つけられたりするわけですね。
√2 なしで X=x-y,Y=x+y とおいた方が,この後の計算が実は楽になったりもするかも

さて,手に入れた新変数を使って解析を進めます。

x^2y+xy^2-x^2-2xy-y^2+x+y=k をX,Yの式で表します。
X^2=の形に直すと少し扱いやすそうなYの関数が得られました。
どちらかというとXとYが逆の方が見栄えがイイデスネ

ついでにXに付いた2乗が邪魔です。
というわけでX^2=y,Y=xという風に更に置き直してしまいました。
Xに付いた2乗を無くしたおかげで楕円が2次関数になっちゃいましたよ

X^2=yとおいたので,y≧0の部分のみを考えなければならないことに注意です。
f(x)=(x-√2)^2-(√2/x)k は,放物線 y=(x-√2)^2 と双曲線 y=(√2/x)k
の各xに対するy座標の差として考えることができますね。
y≧0で考えるので,放物線の方が大きい部分を考えなければなりません。
これでイメージを膨らましながらy=f(x)のグラフを考えてみましょう。
k>0,k=0,k<0の場合に分けて考察します。
まずはk>0の場合を考えますが,放物線 y=(x-√2)^2 と双曲線 y=(√2/x)k は
必ず交点を持つことが分かります

交点のx座標がy=f(x)の零点になるわけですね。
kが大きい時は交点が1個ですが,小さくなると複数になります。
とりあえずy=f(x)のグラフをx>0部分とx<0とに分けて考えて
それぞれが放物線 y=-3x^2+12 と交点を持つようなkの範囲を求めます





続いて,放物線と双曲線が交点を複数持つ場合です。
前回,元の変数のままでkを動かしてグラフの変化を見てみましたが
途中で真ん中に変な島みたいなのが出現しましたよね。
それに相当する部分ですかね,この交点が複数現われて来る現象は~。

kを0に近づけていくとどんどんαは√2に近付いていきます。
だから相変わらずy=f(x)のグラフは放物線 y=-3x^2+12 と交わるんですね。
k=0の時も問題ありません。
k<0の場合もまったく同様に考えます。

というわけでy=f(x)のグラフが放物線 y=-3x^2+12 と交点を持つような
kの範囲を求めることができました


やはり骨が折れますね



試験場でこんな大層なことをやることはまず不可能でしょう

次回はメンドクサイ解法をもう1パターンやってみます(まだやるんかーい
 )
)




















































 前回のはこちら
前回のはこちら