どもども。
今回は今年の京大入試理系数学の第3問をやります
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon3.html
第2問と同様に,誘導とかは無いので自分でアプローチ方法を探らなければなりません。
一番シンプルな発想は, x^2y+xy^2-x^2-2xy-y^2+x+y=k とおいて,
kをパラメータだと思って色々動かします。2次曲線 x^2+xy+y^2=6 と交点を持つような
kの範囲を求めるという方法ですね
しかしまぁ,それは恐ろしく複雑骨折級に骨が折れる作業なのですよ。
骨だけでなく心も折れます
とても試験場でやれる作業ではありません。
ていうか時間があってもやる気が起きません
さて, x^2y+xy^2-x^2-2xy-y^2+x+y も x^2+xy+y^2 も
わかりやすーくx,yの対称式になっていますね~
ということは基本対称式 x+y,xy の多項式で表現できます
そこで,X=x+y,Y=xy とおいて新変数X,Yを主役にして考えてみることにしましょう。
もしかしたら考えやすくなるかも,という期待を込めて
X=x+y,Y=xy という変換はよく使いますが,その際に必ずセットで付いてくるのは
(X,Y)の存在範囲を確かめることですね。
x,yが全実数を動いたとしてもX,Yは全実数を動くわけでは無いんですね~。

1変数Xの3次関数の考察になってしまったので,随分スッキリしましたね

あとはいつものように微分して増減表なりグラフなりを描いて値域を求めておしまいで御座います。

文字の置き換えによって劇的に簡単に解けてしまいましたね~。
では,元の変数のままでやったらどうなるんでしょうか。
最初に挙げたように素朴に x^2y+xy^2-x^2-2xy-y^2+x+y=k とおくパターンです。
位置を比較するもう一方の曲線 x^2+xy+y^2=6 は斜めに傾いた楕円です。
3次曲線 x^2y+xy^2-x^2-2xy-y^2+x+y=k の概形を考えるだけでもしんどいのに
そのあと傾いた楕円と接する条件を考えるのは,もうペンをぶん投げたくなりますね
参考までに,グラフを描いた図を挙げておきます
・k<-8-6√2のとき

赤いのが x^2y+xy^2-x^2-2xy-y^2+x+y=k で
青いのが楕円 x^2+xy+y^2=6 です。
赤い方は何やら3つのパートからなるみたいですね,やはり考察はめんどくさそうです!
・k=-8-6√2のとき

赤と青が接するkの最小値です。赤はだんだん中心に向かって迫ってくるようです。
・-8-6√2<k<0のとき

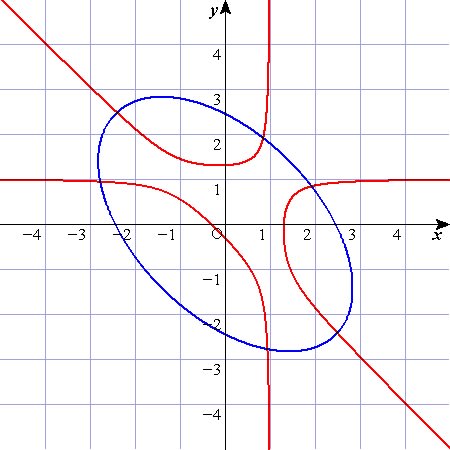
上はk=-8,下はk=-0.4のときです。
このときは赤と青は複数の交点を持っていますね。
・k=0のとき

赤が退化して直線3本になっちゃいました~
そういえば x^2y+xy^2-x^2-2xy-y^2+x+y=(x-1)(y-1)(x-y)
と因数分解できるんですよ
・0<k<3のとき
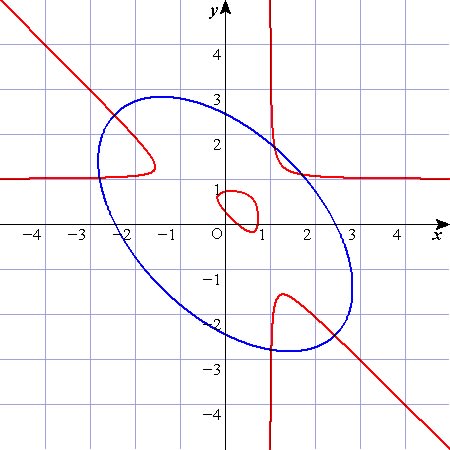

上がk=0.2,下がk=0.4の場合です。
上の方,なんだか真ん中に何かあります
k=0の時の真ん中部分が分離して小さな島のように残っちゃうんですね。
この島はkが大きくなるにつれ小さくなってやがて消滅します。
外側の3つの部分も向きが変わりました。
kが大きくなるにつれてどんどん遠くに向かっていくようです。
・k=3のとき

これが赤と青が接するkの最大値です。
・k>3のとき

赤と青は交点を持たず赤はどんどん中心から遠ざかっていきます。
素朴な手法でこの問題を解くには今挙げたこの変化の様子を
せっせと調べなければいけないわけです。イヤですね~~
せめて楕円の長軸と短軸がx軸とy軸と一致していれば少しは
考察しやすくなるかもなんですが~

というわけで次回は少しメンドクサイ解法でこの問題にトライしてみます。
今回は今年の京大入試理系数学の第3問をやります

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon3.html
第2問と同様に,誘導とかは無いので自分でアプローチ方法を探らなければなりません。
一番シンプルな発想は, x^2y+xy^2-x^2-2xy-y^2+x+y=k とおいて,
kをパラメータだと思って色々動かします。2次曲線 x^2+xy+y^2=6 と交点を持つような
kの範囲を求めるという方法ですね

しかしまぁ,それは恐ろしく複雑骨折級に骨が折れる作業なのですよ。
骨だけでなく心も折れます

とても試験場でやれる作業ではありません。
ていうか時間があってもやる気が起きません

さて, x^2y+xy^2-x^2-2xy-y^2+x+y も x^2+xy+y^2 も
わかりやすーくx,yの対称式になっていますね~
ということは基本対称式 x+y,xy の多項式で表現できます

そこで,X=x+y,Y=xy とおいて新変数X,Yを主役にして考えてみることにしましょう。
もしかしたら考えやすくなるかも,という期待を込めて

X=x+y,Y=xy という変換はよく使いますが,その際に必ずセットで付いてくるのは
(X,Y)の存在範囲を確かめることですね。
x,yが全実数を動いたとしてもX,Yは全実数を動くわけでは無いんですね~。

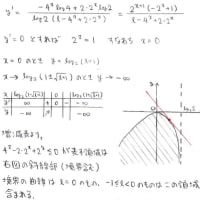
1変数Xの3次関数の考察になってしまったので,随分スッキリしましたね


あとはいつものように微分して増減表なりグラフなりを描いて値域を求めておしまいで御座います。

文字の置き換えによって劇的に簡単に解けてしまいましたね~。
では,元の変数のままでやったらどうなるんでしょうか。
最初に挙げたように素朴に x^2y+xy^2-x^2-2xy-y^2+x+y=k とおくパターンです。
位置を比較するもう一方の曲線 x^2+xy+y^2=6 は斜めに傾いた楕円です。
3次曲線 x^2y+xy^2-x^2-2xy-y^2+x+y=k の概形を考えるだけでもしんどいのに
そのあと傾いた楕円と接する条件を考えるのは,もうペンをぶん投げたくなりますね

参考までに,グラフを描いた図を挙げておきます

・k<-8-6√2のとき

赤いのが x^2y+xy^2-x^2-2xy-y^2+x+y=k で
青いのが楕円 x^2+xy+y^2=6 です。
赤い方は何やら3つのパートからなるみたいですね,やはり考察はめんどくさそうです!
・k=-8-6√2のとき

赤と青が接するkの最小値です。赤はだんだん中心に向かって迫ってくるようです。
・-8-6√2<k<0のとき


上はk=-8,下はk=-0.4のときです。
このときは赤と青は複数の交点を持っていますね。
・k=0のとき

赤が退化して直線3本になっちゃいました~
そういえば x^2y+xy^2-x^2-2xy-y^2+x+y=(x-1)(y-1)(x-y)
と因数分解できるんですよ

・0<k<3のとき


上がk=0.2,下がk=0.4の場合です。
上の方,なんだか真ん中に何かあります

k=0の時の真ん中部分が分離して小さな島のように残っちゃうんですね。
この島はkが大きくなるにつれ小さくなってやがて消滅します。
外側の3つの部分も向きが変わりました。
kが大きくなるにつれてどんどん遠くに向かっていくようです。
・k=3のとき

これが赤と青が接するkの最大値です。
・k>3のとき

赤と青は交点を持たず赤はどんどん中心から遠ざかっていきます。
素朴な手法でこの問題を解くには今挙げたこの変化の様子を
せっせと調べなければいけないわけです。イヤですね~~

せめて楕円の長軸と短軸がx軸とy軸と一致していれば少しは
考察しやすくなるかもなんですが~


というわけで次回は少しメンドクサイ解法でこの問題にトライしてみます。












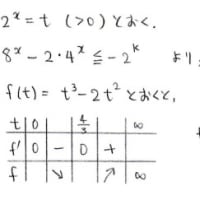



※コメント投稿者のブログIDはブログ作成者のみに通知されます