どもども。
今回からは今年の東北大入試理系数学の問題をやっていこうと思いますです~
と言いますのも,当方,現在宮城県在住なものでして,
そういうのもあってここらで東北大の問題でもやっつけましょう~っていう話なわけであります
そんなわけで今年の問題を見てみますと,
難易度的には並,といった感じで標準的な入試問題っぽいセットになってます。
簡単そうに見せかけといて,意外とうっかりつまずいちゃうかもしれない,
しかもそのまま動揺が止まらなくなってしまうかもしれない,
そんな予感がするのは1,5,6あたり?
落ち着いてやれば決して出来ないことはない問題ですので,頑張って泥沼に沈まないようにしたいところです。
ではでは今回は第1問です
問題はこちら

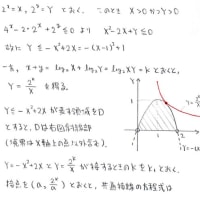
2つのパラメータs,tが動くときの(x,y)の存在領域を求める問題です~
こういうの嫌いな受験生,多いんじゃないでしょうか
考え方は幾つかあるので,その場その場で上手く使い分けられると素敵です
そんな幾つかの考え方を使って解いていってみます。
 考え方1
考え方1
(X,Y)という点が答えの領域に含まれているとしましょう~
ということは,何かしらのs,t(s≧0,t≧0)が存在して
X=s+t+1,Y=s-t-1を満たしているわけですね。
それじゃあ,具体的にその「何かしらのsとt」を求めてしまいましょう という作戦です。
という作戦です。
実際にその「何かしらのsとt」が求められたのなら,
確かにこの(X,Y)という点は答えの領域に含まれているわけだ といえますね。
といえますね。


X=s+t+1,Y=s-t-1を満たす(s,t)がもしも存在するのなら
それはs=(X+Y)/2,t=(X-Y-2)/2 というモノでなければならない。
そして実際にこのようなものが存在するのはX+Y≧0かつX-Y-2≧0という条件を満たしているときである
という理屈ですね~~
 考え方2
考え方2
sとtという2つのパラメータがあるから話がややこしくなるんだ~
じゃあ~1個消しちゃえばいいじゃん~~


という発想です。
x=s+t+1…… ,y=s-t-1……
,y=s-t-1……
の2式を使えばsとtのうち片方を消去することが可能です。
例えば足せばx+y=2s…… ,引けばx-y=2t+2……
,引けばx-y=2t+2……
が得られますね。ただし,注意しなきゃいけないことがあります。
「 かつ
かつ 」という条件は「
」という条件は「 かつ
かつ 」と同値なので,
」と同値なので,
くれぐれも だけを考えておしまいにしないようにしなきゃならんのです
だけを考えておしまいにしないようにしなきゃならんのです
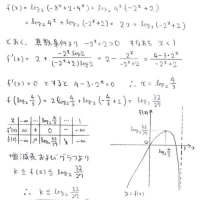
さて, の考察ですが,これはsをパラメータとした直線を表していますね。
の考察ですが,これはsをパラメータとした直線を表していますね。
s(≧0)が動くことによって様々な直線を表します。
これらの直線の合併集合を考えることによって を満たす(x,y)の存在領域が分かります。
を満たす(x,y)の存在領域が分かります。
そこでその合併集合の中で特にx=x_0である部分を考えます。
つまりxを固定する,とか,縦の切り口を考える,とか,そういう作業です
sがあれこれ動いたときにyはどのような範囲を動くでしょうか。
x_0ごとにそれを考えてそれを合体させれば全体の形が分かります。
一方で もまたtをパラメータとした直線群を表しますので,こっちも同じように考察してください。
もまたtをパラメータとした直線群を表しますので,こっちも同じように考察してください。
両方を同時に満たす領域が答えです



上の解答の中では「s≧0,t≧0よりx≧1なので」などと触れていますが
 を考える上ではs≧0だけ考えれば実際は十分です(
を考える上ではs≧0だけ考えれば実際は十分です( にはtとか
にはtとか は無関係なので)。
は無関係なので)。
 考え方3
考え方3
x=s+t+1をs,tに関する2変数関数だと思いましょう。
s≧0,t≧0のときのxの値域はx≧1です
そこでX(≧1)を定数として,x=Xとなる(s,t)全体を考えます。
そのような(s,t)たち限定で2変数関数y(s,t)=s-t-1の値域を求めるという発想です

 考え方4
考え方4
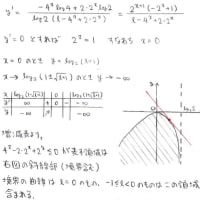
x=s+t+1,y=s-t-1をベクトル表記して
(x,y)=s(1,1)+t(1,-1)+(1,-1) と書いてみましょう
変形して, (x-1,y+1)=s(1,1)+t(1,-1)
この右辺は1次独立なベクトル(1,1)と(1,-1)の1次結合になってるわけですな
普段我々が使うxy座標は,(x,y)=x(1,0)+y(0,1)と書き直すことが出来て,
(1,0)方向の成分がxで(0,1)方向の成分がyであるという解釈が可能でした
それと同じ考えをすればいいんですね~


長くなってきたので(2)は次回に回します~
今回と同じような手法などでやっていきます~
今回からは今年の東北大入試理系数学の問題をやっていこうと思いますです~

と言いますのも,当方,現在宮城県在住なものでして,
そういうのもあってここらで東北大の問題でもやっつけましょう~っていう話なわけであります

そんなわけで今年の問題を見てみますと,
難易度的には並,といった感じで標準的な入試問題っぽいセットになってます。
簡単そうに見せかけといて,意外とうっかりつまずいちゃうかもしれない,
しかもそのまま動揺が止まらなくなってしまうかもしれない,
そんな予感がするのは1,5,6あたり?

落ち着いてやれば決して出来ないことはない問題ですので,頑張って泥沼に沈まないようにしたいところです。
ではでは今回は第1問です

問題はこちら

2つのパラメータs,tが動くときの(x,y)の存在領域を求める問題です~

こういうの嫌いな受験生,多いんじゃないでしょうか

考え方は幾つかあるので,その場その場で上手く使い分けられると素敵です

そんな幾つかの考え方を使って解いていってみます。
 考え方1
考え方1(X,Y)という点が答えの領域に含まれているとしましょう~

ということは,何かしらのs,t(s≧0,t≧0)が存在して
X=s+t+1,Y=s-t-1を満たしているわけですね。
それじゃあ,具体的にその「何かしらのsとt」を求めてしまいましょう
 という作戦です。
という作戦です。実際にその「何かしらのsとt」が求められたのなら,
確かにこの(X,Y)という点は答えの領域に含まれているわけだ
 といえますね。
といえますね。

X=s+t+1,Y=s-t-1を満たす(s,t)がもしも存在するのなら
それはs=(X+Y)/2,t=(X-Y-2)/2 というモノでなければならない。
そして実際にこのようなものが存在するのはX+Y≧0かつX-Y-2≧0という条件を満たしているときである

という理屈ですね~~
 考え方2
考え方2sとtという2つのパラメータがあるから話がややこしくなるんだ~

じゃあ~1個消しちゃえばいいじゃん~~



という発想です。
x=s+t+1……
 ,y=s-t-1……
,y=s-t-1……
の2式を使えばsとtのうち片方を消去することが可能です。
例えば足せばx+y=2s……
 ,引けばx-y=2t+2……
,引けばx-y=2t+2……
が得られますね。ただし,注意しなきゃいけないことがあります。
「
 かつ
かつ 」という条件は「
」という条件は「 かつ
かつ 」と同値なので,
」と同値なので,くれぐれも
 だけを考えておしまいにしないようにしなきゃならんのです
だけを考えておしまいにしないようにしなきゃならんのです
さて,
 の考察ですが,これはsをパラメータとした直線を表していますね。
の考察ですが,これはsをパラメータとした直線を表していますね。s(≧0)が動くことによって様々な直線を表します。
これらの直線の合併集合を考えることによって
 を満たす(x,y)の存在領域が分かります。
を満たす(x,y)の存在領域が分かります。そこでその合併集合の中で特にx=x_0である部分を考えます。
つまりxを固定する,とか,縦の切り口を考える,とか,そういう作業です

sがあれこれ動いたときにyはどのような範囲を動くでしょうか。
x_0ごとにそれを考えてそれを合体させれば全体の形が分かります。
一方で
 もまたtをパラメータとした直線群を表しますので,こっちも同じように考察してください。
もまたtをパラメータとした直線群を表しますので,こっちも同じように考察してください。両方を同時に満たす領域が答えです




上の解答の中では「s≧0,t≧0よりx≧1なので」などと触れていますが
 を考える上ではs≧0だけ考えれば実際は十分です(
を考える上ではs≧0だけ考えれば実際は十分です( にはtとか
にはtとか は無関係なので)。
は無関係なので)。 考え方3
考え方3x=s+t+1をs,tに関する2変数関数だと思いましょう。
s≧0,t≧0のときのxの値域はx≧1です

そこでX(≧1)を定数として,x=Xとなる(s,t)全体を考えます。
そのような(s,t)たち限定で2変数関数y(s,t)=s-t-1の値域を求めるという発想です


 考え方4
考え方4x=s+t+1,y=s-t-1をベクトル表記して
(x,y)=s(1,1)+t(1,-1)+(1,-1) と書いてみましょう

変形して, (x-1,y+1)=s(1,1)+t(1,-1)
この右辺は1次独立なベクトル(1,1)と(1,-1)の1次結合になってるわけですな

普段我々が使うxy座標は,(x,y)=x(1,0)+y(0,1)と書き直すことが出来て,
(1,0)方向の成分がxで(0,1)方向の成分がyであるという解釈が可能でした

それと同じ考えをすればいいんですね~



長くなってきたので(2)は次回に回します~

今回と同じような手法などでやっていきます~













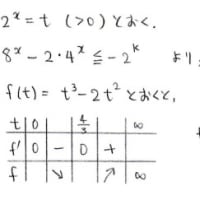



※コメント投稿者のブログIDはブログ作成者のみに通知されます