どもども。こんにちは。
今日もゆるゆる~と頑張りましょう。
前回の2012年東大入試理系数学第2問を取り上げましたので
今回は第3問をやります
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon3.html
標準的な回転体の問題だと思います。東大は元々空間図形の問題を好んで
出題する傾向がありますが,今年の問題はとてもシンプルな出題じゃないかと
思います。(2)はオマケみたいなものでしょうか
まずは領域Sの概形を確認してみます。

これをx軸方向に1回転させた立体の体積がV_1,y軸方向に1回転させた立体の体積がV_2です。この2つを求めます。まずはV_1からいきましょう。
対称性より,0≦x≦1/2の部分を考えて2倍すればいいですね。
スタンダードな解法としては平面x=tでこの回転体を切ったときの断面積を
0から1/2まで積分するというものが考えられます。
この断面はレコード状の円環になっています。
V_2に関しても同様で,今度は平面y=tで切断した時の断面積を
0から1/(4√2)まで積分します。こちらの断面は円になっていますね。

この問題に関しては素直に上記のやり方で計算するのが簡単そうです。
次は,俗に「バウムクーヘン」や「年輪」や「かつら剥き」などと呼ばれる
積分を使った解法をやってみましょう。
それはどういうものかと言いますと,例えばy=f(x)(0≦x≦a)で与えられた曲線をy軸周りに1回転させて出来る回転体の体積を考えるとき,
原点を中心とした半径tの円を底面とする高さf(t)の円柱の側面積をtに
関して0からaまで積分するというアイデアです。
幾重にも円柱の側面が重なり合ってる様子はまるでバウムクーヘンや木の年輪のようですね。
受験数学の裏技という位置付けもされますが,説明なしにこの考えを使っていいのかという意見もあるので,今回の問題のように標準的な手法でやっても難しくなさそうなときは試験では標準的な手法を使う方が無難かもしれないですね。

では実際に使ってみます

お。なかなか簡単ですね
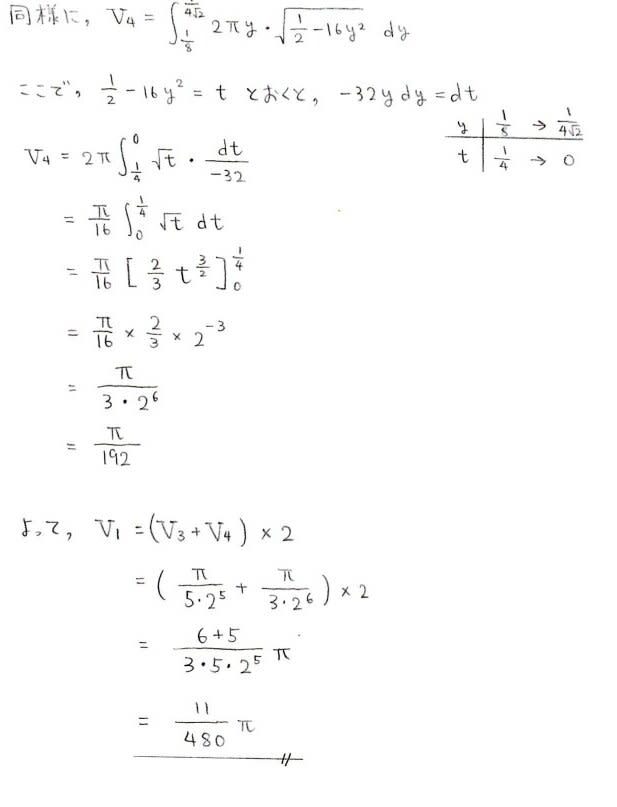

無理関数の積分なんかが出てくるので,若干面倒??
次回は極座標を用いてこの計算をやってみます
最後に(2)をやってしまいましょう。
V_1とV_2の比と1の大小関係を問う問題です。
ダイレクトに比を計算するか,V_1とV_2の大小関係を比べるか。
パッと思いつくのは大体このどちらかでしょうか。


√2の近似値として1.42を用いる際は
「1.41^2<2<1.42^2より」なんて一言を添えとくと親切かも。
22-5(8√2-7)=57-40√2=√3249-√3200>0
とする手もありますね。
ではでは。
今日もゆるゆる~と頑張りましょう。
前回の2012年東大入試理系数学第2問を取り上げましたので
今回は第3問をやります

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon3.html
標準的な回転体の問題だと思います。東大は元々空間図形の問題を好んで
出題する傾向がありますが,今年の問題はとてもシンプルな出題じゃないかと
思います。(2)はオマケみたいなものでしょうか

まずは領域Sの概形を確認してみます。

これをx軸方向に1回転させた立体の体積がV_1,y軸方向に1回転させた立体の体積がV_2です。この2つを求めます。まずはV_1からいきましょう。
対称性より,0≦x≦1/2の部分を考えて2倍すればいいですね。
スタンダードな解法としては平面x=tでこの回転体を切ったときの断面積を
0から1/2まで積分するというものが考えられます。
この断面はレコード状の円環になっています。
V_2に関しても同様で,今度は平面y=tで切断した時の断面積を
0から1/(4√2)まで積分します。こちらの断面は円になっていますね。

この問題に関しては素直に上記のやり方で計算するのが簡単そうです。
次は,俗に「バウムクーヘン」や「年輪」や「かつら剥き」などと呼ばれる
積分を使った解法をやってみましょう。
それはどういうものかと言いますと,例えばy=f(x)(0≦x≦a)で与えられた曲線をy軸周りに1回転させて出来る回転体の体積を考えるとき,
原点を中心とした半径tの円を底面とする高さf(t)の円柱の側面積をtに
関して0からaまで積分するというアイデアです。
幾重にも円柱の側面が重なり合ってる様子はまるでバウムクーヘンや木の年輪のようですね。
受験数学の裏技という位置付けもされますが,説明なしにこの考えを使っていいのかという意見もあるので,今回の問題のように標準的な手法でやっても難しくなさそうなときは試験では標準的な手法を使う方が無難かもしれないですね。

では実際に使ってみます


お。なかなか簡単ですね

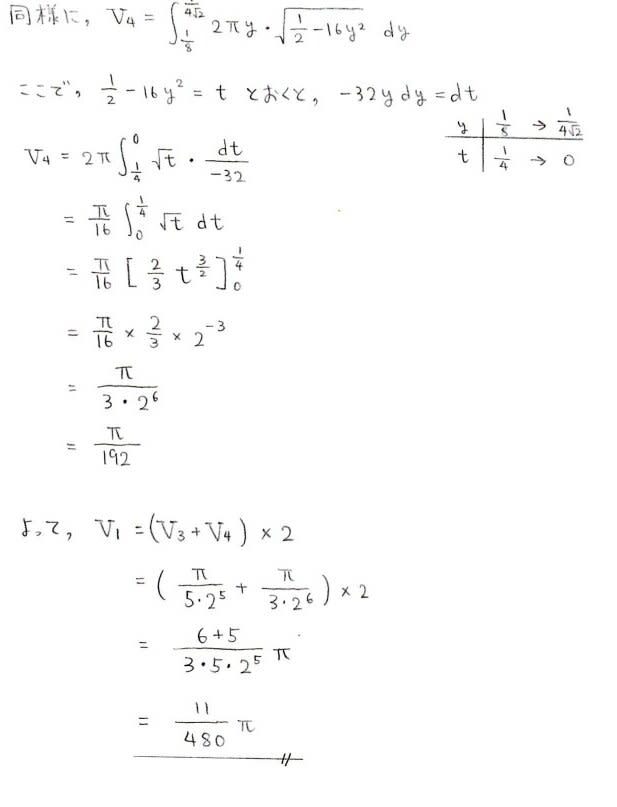

無理関数の積分なんかが出てくるので,若干面倒??
次回は極座標を用いてこの計算をやってみます
最後に(2)をやってしまいましょう。
V_1とV_2の比と1の大小関係を問う問題です。
ダイレクトに比を計算するか,V_1とV_2の大小関係を比べるか。
パッと思いつくのは大体このどちらかでしょうか。


√2の近似値として1.42を用いる際は
「1.41^2<2<1.42^2より」なんて一言を添えとくと親切かも。
22-5(8√2-7)=57-40√2=√3249-√3200>0
とする手もありますね。
ではでは。















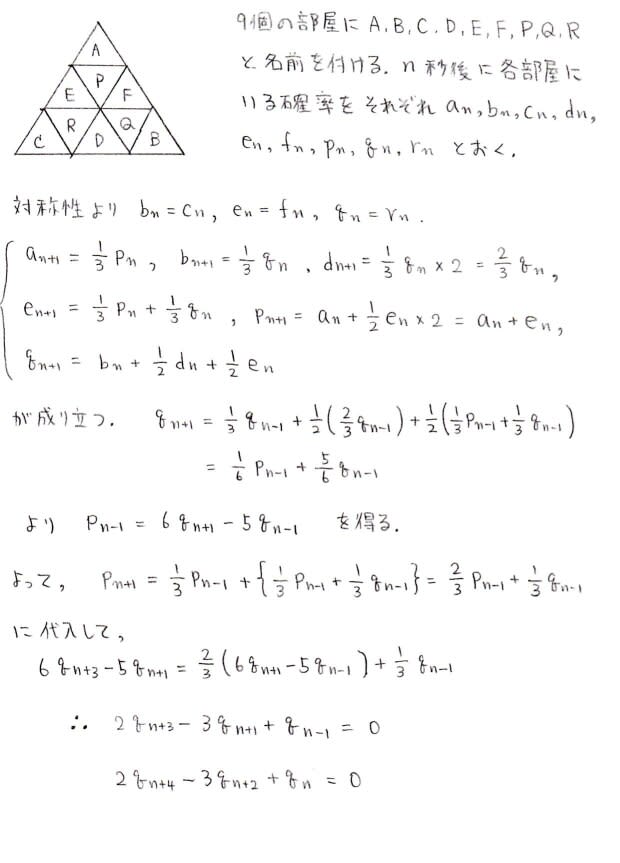









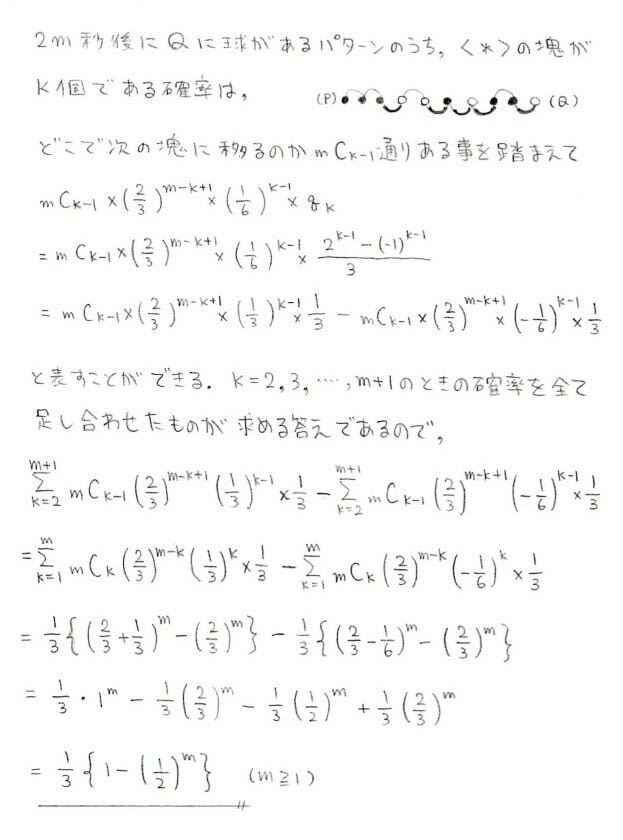

















 追記(2012年11月15日)
追記(2012年11月15日)