ファインマン物理学 I: 第13章、第14章

第１３章：仕事と位置のエネルギー

運動エネルギーと位置エネルギーの和が常に一定だということを数式を使った具体例を学ぶのがこの章だ。エネルギーの変化量が仕事の量に一致しているということを述べ、力学法則と仕事や仕事率の数量的関係も明らかにしている。日常的によく耳にするワット（W）とジュール（J）も例題の中で紹介される。「ジュール」は物理学で使う熱量の単位で簡単に「カロリー」としての値を求めることができる。

第１２章で「力とは何か？」という難しい問題を考えた後だけに、日常的な物理量がすっきりと計算できるのを見るのは楽しいものだ。

運動エネルギーの式は微分すると Fv になり、これが「仕事率」と呼ばれるものになる。Fとvは本来はベクトル量なので掛け算は内積 F・v として計算することになる。計算結果は「仕事率」でスカラー量だ。

力 F は時々刻々変わるベクトル量だから、引っ張られる（または押される）物体の運動の道筋に沿って線積分するとそれはその力が行った「仕事」を計算することになる。「仕事」のことを「仕事量」と呼ぶ場合もあるが、大事なのはこれがエネルギーと同じ単位であることだ。エネルギーを時間で微分して、その後積分したのだから当然と言えばそれまでだが。

力 F が鉛直方向で一定の場合、それは「地表面の近くの落体の運動」という例にあてはめて考えられるから、その物体の運動前と運動後の高さの差 h とすると仕事の量は mgh となる。つまり鉛直距離だけが位置エネルギーに関係してくるのだ。

次に取り上げるのが引力によってなされる仕事を計算することだ。地表面では引力の値はほぼ一定なので計算は前の例のように高さの差だけで求められるが、地球の中心からの距離 r が大きいと力 F は万有引力の法則の計算式を使わなければならない。

万有引力の法則は r について逆２乗に比例するから、この式を物体の運動前から運動後の位置まで積分する。ファインマン先生が図示して説明するところによると、この積分はどんな経路を通ったとしても運動前後の位置、それも地球の中心からの距離だけで決まる値となるのだ。つまり積分は簡単な r について逆２乗関数の定積分となり簡単に求めることができる。

その後、多数の天体が相互に引力を及ぼしあっている場合には位置エネルギーをそれぞれの天体について合計すればよいことを比較的こみいった計算で求めている。

この章の最後の２つの例題は興味深いものだ。１つは引力をもたらす物体が無限に広がる平面に分布し、引力を受ける物体がその平面から距離 a にある場合。おもしろいことに物体に働く引力 F は距離 a には関係なく一定になるのだ。静電磁気学のクーロンの法則が万有引力の法則と同じ形をしていることから、この例題は無限に広がる平面電荷による電場に置かれた電荷に及ぼす力という問題に適用することができる。重力と電磁気力は同じ数式展開で解ける問題が多い。

最後の例題がいちばん興味深い。ニュートンの質点定理を証明してみせるのだ。引力を与える物体が球体のとき、その全質量は球の中心の「質点」という大きさのない点に集中していると考えて万有引力の法則を適用してよい、というのが質点定理だ。以前このブログでも「これがニュートンの質点の定理の証明だ！」という記事で紹介したが、この方法とは別の手順でファインマン先生は証明してみせるのだ。この証明のポイントは地球の中心からある物体 m' の位置エネルギーを元にしていることだ。興味のある方は「とね日記（数式の部屋）」の「ニュートンの質点定理の証明（ファインマン物理学 I, 191pより）」というページ掲載しておいたのでご覧になるとよい。２つの証明方法を比べてみるのもおもしろいだろう。


第１４章：仕事と位置のエネルギー（結び）

この章の冒頭でファインマン先生は勉強のしかたについて学生にアドバイスをする。物理学や数学ではいろいろ公式や証明がでてくるが、その公式や証明に使われる技巧を覚えることよりも、その背景にあるしくみを理解しその上で自分で結論を導き出すことのほうが大切だと説いている。学んでいく課程で大切なのは公式や証明を構成するそれぞれの事柄の関係を理解することなのだ。

前の章で述べた力によってなされる「仕事」というものが動かされる物の位置の差からだけで決まるというのが物理学の意味での「仕事」だ。日常的には重たい物を踏ん張って支えているだけでも疲れるから、これは仕事をしたと思われがちである。確かにこの場合は筋肉のエネルギーを消費するのだが、これは腕の筋肉が緊張するためだけにもエネルギーを必要としているからだ。けれども物理学では物体が移動しなければ仕事はしていないことになる。

ファインマン先生は次に「束縛された運動」について説明をする。物体の運動というものは何も力が働かないと慣性の法則によって直線運動をする。進行方向とは異なる方向に力が働くと、物体には方向を含めた意味での加速度が生じて運動方向や速度が変化するわけだ。このとき速度の方向に直角な方向に働く力の成分はこの物体のエネルギーには全く寄与しない。物体の運動方向に一致する力の成分だけが仕事をする。

物体の速度に直角な方向に作用して物体に加速度を与えて進路を変えることが物体に対する「束縛」なのである。わかりやすい例をあげよう。第４章のエネルギー保存則のところでジェットコースターの運動を取り上げた。



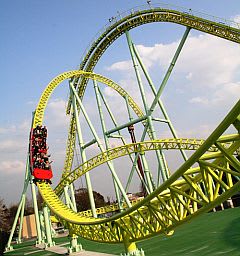
摩擦力や空気抵抗が無視できるとき、同じ高さにあるコースターは同じ運動エネルギー、同じ位置エネルギーを持つから速度は等しいことを述べた。コースターは軌道に従って走らなければならない。つまりコースターの走る方向を束縛しているわけだ。この束縛の力はレールからコースターの車輪に直角方向から働いている。つまり真横からの力なので、コースターに対しては何の仕事、つまりエネルギーを与えたり奪ったりしていない。これが運動エネルギーと位置エネルギーだけを考えれば十分であることを示している。

太陽の周りを回る地球についても同様だ。太陽が地球を引っ張る引力は常に地球の進行方向に対して直角である。太陽が地球を束縛してその運動方向を変えているだけなのだ。運動エネルギーと位置エネルギーの和は常に一定なので、いつまでも地球は太陽の周りをまわりつづけることができる。

次は「保存力」についてだ。保存力について特徴的なのは物体が移動する道すじのたどり方によって無関係であるということだ。つまり移動前と移動後の位置だけに仕事やエネルギーの変化が依存しているということである。道すじに関係なく位置エネルギーは位置の関数 U(x) であらわされるのはことためだ。保存力だけしかはたらいていないならば、運動エネルギー T と位置エネルギー U の和は一定であるということになる。経路のとりかたによらないのが保存力であるならば、２点を結ぶ「行き」と「帰り」に必要な仕事は大きさが等しく符号は反対になる。つまり保存力においては運動を１周すると仕事の合計はゼロになる。

位置エネルギーは太陽などの天体のほか、バネのつりあいの位置からの変位、電荷からもうひとつの電荷までの距離などさまざまである。「力学は本当に簡単か？（球の衝突実験）」という記事で紹介したガウス加速器も「磁力による位置エネルギー」が運動エネルギーに変化したことによって説明される。

力のあるところには必ず位置エネルギーがあるのだ。

反対に保存しない力、つまり「非保存力」についてはどうだろう。摩擦力や空気抵抗がある場合、運動エネルギーが熱エネルギーになってしまい、T+U の値は減ってしまうことがある。これは運動エネルギーが物体の原子の振動エネルギーになって熱という現象を起こしているわけだから、詳しく考えれば原子の運動エネルギーになっていると解釈することもできるわけだ。厳密に言えばこれは正確ではないのだそうだが、大まかに言って熱に変化するような「非保存力」も実はそう見えるだけで本当のところは「保存力」であるのだ。

最後にポテンシャルや場ということについて考えてみる。第１２章で「場」というものについて定性的な（直観的な）説明をしていたが、この章の計算によって「場」は定量的（具体的）なものとして理解できるようになる。

質量 m の物体に働く力 F は物体の３次元座標 (x, y, z) だけで決まる位置によって表されるから、F = mC(x,y,z) となる。Cがいわゆる「場」と呼ばれベクトル量になるわけだ。Cという「場」の方向が力の向きである。

位置エネルギーも同じように扱うことができる。(力 F)x(ds) の積分は (場 C)x(ds) の積分と書くことができる。両者は比例定数ぶんだけ異なるだけだから空間の点 (x, y, z) にあるひとつの物体の位置エネルギーは、ある関数を m にかけたものと書ける。その関数のことをポテンシャル Ψ というのである。つまり U(x, y, z) =mΨ(x,y,z) である。注意すべきは C(x,y,z) が Ψ(x,y,z) に置き換わっただけではないことだ。C(x,y,z)がベクトル関数であるのに対し Ψ(x,y,z) がスカラー関数であるからだ。これは計算を非常に楽にし、ΨのほうがCよりも取り扱いがずっと易しくなるのである。

ポテンシャル U(x,y,z) に関連してファインマン先生は物体に働く力 F を座標成分であらわす方法を紹介する。力 F と微小変位 ds の内積の積分がポテンシャルの微小変位 -ΔU に等しいことから次の式を得る。この段階で偏微分記号 ∂ や勾配 ∇ の記号が登場する。すなわち力 F の３成分は次のようになる。

Fx = -∂U/∂x
Fy = -∂U/∂y
Fz = -∂U/∂z

Cの３成分も次のように書き表せる。

Cx = -∂Ψ/∂x
Cy = -∂Ψ/∂y
Cz = -∂Ψ/∂z

勾配(gradient)は次のように書き表せる。これは１つのスカラーに作用してベクトルを作る演算子である。∇=∂/∂x + ∂/∂y + ∂/∂zである。∇はベクトルなのでむしろ ∇=(∂/∂x,∂/∂y,∂/∂z) と書いたほうがよいかもしれない。

すなわち上記の６つの式は次のようになる。FとCはベクトル、Uとψはスカラー関数であることに注意。

F = -∇U
C = -∇Ψ

最後に場とポテンシャルの例として電気の場合について紹介している平行板コンデンサの電場、エネルギー、ポテンシャル、仕事などについての関係からポテンシャルの差が電位差（ボルト）になることを述べてこの章をしめくくっている。電位差は平行金属板の距離に比例して大きくなる。雷が大きな電圧を持つのはこのためである。

金属球殻内部の電場がゼロになることもこの部分で説明されている。電場は球殻の外にしかない。落雷を受けても車内にいるドライバーが何も感じないのはこの理由による。金属球内部の電場がゼロになることはこのページでわかりやすく視覚化されているのでご覧いただきたい。

今日解説した２つの章は数式がメインなので言葉だけで説明するのがむずかしい。なので大雑把に説明するにとどめた。詳細はぜひ本のほうで確認してほしい。


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。
　　


「ファインマン物理学」のレビューを参照したい方、購入したい方はそれぞれ画像をクリックしてください。