
3次元空間で交わる立体?
空間の次元で全く違う常識
前回の記事の重要な部分に大きな誤りがありましたので、訂正記事を書かせていただきます。ご指摘いただいたhirotaさん、ふくちゃん、ありがとうございました。
間違っている箇所は「多次元空間で交わる2つの物体の共通部分の次元数」の説明と結果です。この連載記事では具体的に布やひもなどを使って直観的な説明を心がけていたので、僕自身が「3次元空間の常識の罠」にからめとられてしまいました。
4次元以上の空間で正しい結果を導くためには直観はたよりになりません。この記事では直観に頼らず「座標」の考え方を使って説明します。その結果、多次元空間ではより直観に反する不思議な状況になっていることがおわかりになると思います。
前回間違ってしまった原因は2つあり、どちらも3次元空間の直観が災いしていました。その2つとは次のことです。
1)物体の「重なり」と「交わり」の定義があいまいだったこと
僕は「重なり」と「交わり」の2つに分類したわけですが、現実はもっとたくさんの方法で物体どうしは交わります。そして、複数ある交わり方の方法のうち、どれがいちばん「一般的」かということを慎重に決めなければいけないのです。
2)3次元空間までで成り立つ幾何学的な常識を、そのまま4次元以上の空間に拡張したこと
空間は次元が違うと幾何学的な常識も異なってきます。前回の記事では物体どうしの交わりで「どのようなものが一般的といえるか」という点で、3次元空間までで成り立つ常識を、そのまま4次元以上の空間での状況にあてはめてしまいました。
このように考え方に誤りがあったため、結果も異なってきます。たまたま結果が一致しているケースもありますが、今回の説明にしたがって確認しなおす必要があります。(幸い連載記事のそれ以前の回に対する矛盾は生じていませんでした。)
前回は次の結果をご紹介しました。
「空間の次元数にかかわらず面と面の交わりは線です。」
「空間の次元数にかかわらず立体と立体の交わりは面です。」
けれども正しい結果は、次のようになります。空間の次元が違うと同じ物体どうしても結果は異なりますので、物体が置かれている空間の次元数を示しておく必要があります。
「4次元空間では面と面の交わりは点です。」
「5次元空間では立体と立体の交わりは線です。」
今回の記事では、たくさんある物体の次元の組み合わせのうち、次の4つのケースを例にとって説明させていただきます。
- 3次元空間で交わる面と面
- 4次元空間で交わる面と面
- 5次元空間で交わる立体と立体
- 6次元空間で交わる面と立体
そして現実の世界では物体と物体は貫通する形で交わりませんが、この記事は数学としての話なので貫通してよいことにします。(それに、もし片方の物体を空間と考えれば貫通しても構わないですよね。)
3次元空間で交わる面と面
3次元ユークリッド空間で平面と平面の位置関係には、次の3つの場合が考えられます。平面は無限の彼方まで広がっているとします。
1)平行な場合。(このとき平面は交わらないので今回の記事では除外します。)
2)一致してしまう場合。(全く同じ平面として重なる場合)
3)ひとつの直線に沿って交わる場合。
このうち3)の「ひとつの直線に沿って交わる場合」が平面と平面の位置関係で、もっとも「一般的」な状況と考えます。無作為に2つの平面を3次元空間に「投げ入れた」場合、3)の状況がいちばんおきやすいからです。
3)のケースでもいろいろな角度で交わるわけですが、2つの平面の共通部分の次元を求めることを目的とするならば、次のような状況を考えれば十分です。

この図で赤で示したx-z平面(部屋でいえば床になります)と青で示したy-z平面(部屋でいえば壁)の共通部分はx軸となります。
このことを座標を使って導いてみましょう。簡単なケースですが4次元以上でも同じ手順を使いますので、きちんと覚えてください。
3次元空間で
赤のx-z平面のことを (x, 0, z) とあらわします。
青のy-z平面のことを (0, y, z) とあらわします。
2つの平面の共通部分は x=0 と y=0 という2つの条件を同時に満たさなければならないことがわかります。
したがって共通部分は (0, 0, z) と表されることになり、これは z軸 そのもので、直線であることがわかります。
おわかりになりましたでしょうか?
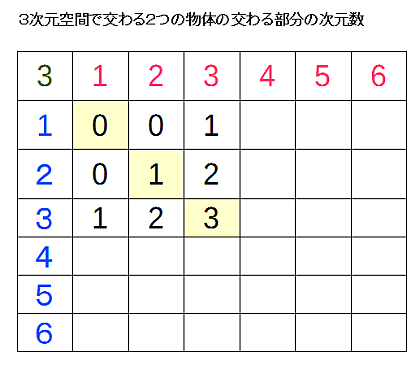
同じ方法で、点や線、面、立体などの組み合わせで2つの物体が交わるケースで表にしました。ご自身でこの表を作ってみるとよいでしょう。
緑色で示した3は空間の次元数、赤と青は物体の次元数、黒は共通部分の次元数です。私たちの直観に一致していることがわかりますね。
4次元空間で交わる面と面
4次元ユークリッド空間で平面と平面の位置関係には、次の4つの場合が考えられます。
1)平行な場合。(このとき平面は交わらないので今回の記事では除外します。)
2)一致してしまう場合。(全く同じ平面として重なる場合)
3)ひとつの直線に沿って交わる場合。
4)ひとつの点で交わる場合。
4)は3次元空間まででは経験することができませんから、私たちには理解できない幾何学的な関係です。
このうち4)の「2つの平面がひとつの点で交わる場合」が平面と平面の位置関係で、もっとも「一般的」な状況と考えます。無作為に2つの平面を4次元空間に「投げ入れた」場合、4)の状況がいちばんおきやすいからです。
4)のケースでもいろいろな角度で交わるわけですが、2つの平面の共通部分の次元を求めることを目的とするならば、座標の原点を含んでいるお互いに直交している、「赤に塗ったx-y平面」と「青に塗ったz-u平面」だけを考えれば十分です。
さっそく座標を使って導いてみましょう。4次元空間上の位置は (x, y, z, u) であらわされることに注意してください。
4次元空間で
赤のx-y平面のことを (x, y, 0, 0) とあらわします。
青のz-u平面のことを (0, 0, z, u) とあらわします。
2つの平面の共通部分は x=y=0 と z=u=0 という2つの条件を同時に満たさなければならないことがわかります。
したがって共通部分は (0, 0, 0, 0) と表されることになり、これは4次元空間の座標の原点そのもので、「点」となります。
同じ方法で、点や線、面、立体、4次元物体などの組み合わせで2つの物体が交わるケースを表にしました。
緑色で示した4は空間の次元数、赤と青は物体の次元数、黒は共通部分の次元数です。

5次元空間で交わる立体と立体
5次元ユークリッド空間で立体と立体の位置関係には、次の4つの場合が考えられます。4次元空間のときと異なり「5)ひとつの点で交わる場合」はありません。
1)平行な場合。(このとき立体は交わらないので今回の記事では除外します。)
2)一致してしまう場合。(全く同じ立体として重なる場合)
3)ひとつの平面で交わる場合。
4)ひとつの直線に沿って交わる場合。
4)の「ひとつの直線に沿って交わる場合」が立体と立体の位置関係で、もっとも「一般的」な状況と考えます。無作為に2つの立体を5次元空間に「投げ入れた」場合、4)の状況がいちばんおきやすいからです。
4)のケースでもいろいろな角度で交わるわけですが、2つの立体の共通部分の次元を求めることを目的とするならば、座標の原点を含んでいるお互いに直交している、「赤に塗ったx-y-z立体」と「青に塗ったz-u-v立体」だけを考えれば十分です。
さっそく座標を使って導いてみましょう。5次元空間上の位置は (x, y, z, u, v) であらわされることに注意してください。
5次元空間で
赤のx-y-z立体のことを (x, y, z, 0, 0) とあらわします。
青のz-u-v立体のことを (0, 0, z, u, v) とあらわします。
2つの立体の共通部分は x=y=0 と u=v=0 という2つの条件を同時に満たさなければならないことがわかります。
したがって共通部分は (0, 0, z, 0, 0) と表されることになり、これは5次元空間の座標のz軸であり「直線」となります。
同じ方法で、点から5次元物体の組み合わせで2つの物体が交わるケースを表にしました。
緑色で示した5は空間の次元数、赤と青は物体の次元数、黒は共通部分の次元数です。

6次元空間で交わる面と立体
6次元ユークリッド空間で面と立体の位置関係には、次の4つの場合が考えられます。
1)平行な場合。(このとき立体は交わらないので今回の記事では除外します。)
2)ひとつの平面で交わる場合。
3)ひとつの直線に沿って交わる場合。
4)ひとつの点で交わる場合
4)の「ひとつの点で交わる場合」が面と立体の位置関係で、もっとも「一般的」な状況と考えます。無作為に面と立体を6次元空間に「投げ入れた」場合、4)の状況がいちばんおきやすいからです。
4)のケースでもいろいろな角度で交わるわけですが、2つの立体の共通部分の次元を求めることを目的とするならば、座標の原点を含んでいるお互いに直交している、「赤に塗ったx-y平面」と「青に塗ったu-v-w立体」だけを考えれば十分です。
さっそく座標を使って導いてみましょう。6次元空間上の位置は (x, y, z, u, v, w) であらわされることに注意してください。
6次元空間で
赤のx-y平面のことを (x, y, 0, 0, 0, 0) とあらわします。
青のu-v-w立体のことを (0, 0, 0, u, v, w) とあらわします。
2つの物体の共通部分は x=y=0 と u=v=w=0 という2つの条件を同時に満たさなければならないことがわかります。
したがって共通部分は (0, 0, 0, 0, 0, 0) と表されることになり、これは6次元空間の座標の原点であり「点」となります。
同じ方法で、点から6次元物体の組み合わせで2つの物体が交わるケースを表にしました。
緑色で示した6は空間の次元数、赤と青は物体の次元数、黒は共通部分の次元数です。

ご理解いただけましたでしょうか?このように各次元で空間や物体の一般常識はずいぶん違うことがおわかりだと思います。
これらの表を使えば、多次元空間に存在する多次元の物体が私たちからどのような次元の物体に見えるか、ということがわかります。
たとえば5次元空間で2つの立方体が絡まっている場合、5次元の表の青の3次元と赤の3次元のマスを見て交わりが1次元であることがわかります。それは私たちからその立方体が1次元のひもとして見えることを意味します。
5次元空間で絡むのは立体、4次元空間で絡むのは面、3次元空間で絡むのはひもでしたよね?表をたどっていくと5次元空間での立体は4次元空間では面として観測され、4次元空間での面は3次元空間ではひもとして観測されることがわかります。高次元空間で絡み合っている2つの物体が低い次元で絡み合っているかどうかは、また別の話になりますが。
多次元空間で物体どうしの位置関係がなぜわかるのか?そしてどれが一般的なものがわかるのはなぜか?と不思議に思われる方がいらっしゃるかもしれません。そのような方は、今回の方法をもう一度よく確認してみてください。
たとえば、空間の次元の座標 (○,○,○,○)の入れ物の中にx, y, zなどいくつの文字を入れるか、そして2つの物体の座標を入れたとき空間の次元の座標成分の個数が足りるのか、足りないのか、ちょうどよいのか、2つの物体の座標を入れるときの場合の数を調べてどのケースが多いかを調べれば、おわかりになると思います。
また、数式は使わないと約束したので書きませんでしたが、共通部分の次元は次の式で計算することができます。今回の手順を理解できていれば、すぐ導ける式です。
共通部分の次元数 = 赤い物体の次元数 + 青い物体の次元数 - 空間の次元数
計算結果がマイナスになるときは0(ゼロ)を計算結果として採用してください。
今回の結果は前々回までの記事で導いた以下のこととも、幸いなことに整合性がとれています。間違いの影響が他の記事に及ばなかったので、ひと安心ですね。
- 4次元空間に1次元物体を置くと一般的に3次元空間からは0次元の点として観測される。
- 4次元空間に2次元物体を置くと一般的に3次元空間からは1次元の曲線として観測される。
- 4次元空間に3次元物体を置くと一般的に3次元空間からは2次元の曲面として観測される。
「座標」の考え方はデカルトによって発明されました。(ルネ・デカルトにより1637年に発表された『方法序説』において平面上の座標の概念を確立され、幾何学と解析学(微積分学)が結びつけられました。)
座標は誰でも考えつきそうなものだし、なぜこれが大発明なのかと不思議に思う方がいらっしゃるかもしれません。けれども、直観に頼らずに座標を使うことから得られる恩恵が絶大なものであることが、今回の例でおわかりいただけたと思います。
次回の記事では、もうひとつ別の例を使って「4次元空間に2次元物体を置くと一般的に3次元空間からは1次元の曲線として観測される。」が成り立っていることをご説明いたします。
応援クリックをお願いします!

























すっきりしました。僕は重なりの次元がマイナスになったら「動ける余裕」が増すことに気が付いていませんでした。
ご説明いただき、ありがとうございます。
この状況をもう少しよく考えてみて、記事として書けるかどうか決めることにしたいと思っています。
数式上で「重なりの次元」が-nになったら「ぶつからず動ける余裕」がn次元と解釈できるだけです。
やはり3次元空間だけでの話ではないですね。
共通部分の次元がマイナスnという負の次元にして調整するというのがよくわかりませんが、空間の次元数で「負」というのはどのようなものでしょうか?ネット検索するとトンデモなページがヒットしてしまいますが、まともな解説をしているページも見受けられます。気になったのは次の2つの解説ですが、hirotaさんがおっしゃっている負の次元とはどのようなものですか?
トポロジ-で負の次元という概念はありますか
http://otasuke.goo-net.com/qa8941216.html
空間を意識した場合の負の次元
http://soudan1.biglobe.ne.jp/qa4647617.html
共通部分の次元が-nとなる高次元にすれば調整で可能になるという話です。
「調整」とはそのようなことをおっしゃっていたのですね。理解いたしました。教えていただきありがとうございます。
厳密にいえばひもとひもが絡むのは、この記事で説明している物体と物体がお互いを突き抜けるようなタイプの交わりではありませんね。ひもの絡みは「交差」と表現したほうがよかったかもしれません。
> 絡み合うとか金庫破りとかは交わらない場合だったはずですが、もうそこには戻らないのですか?
はい、今後予定している記事では「なぜどんどん絡んでいくか」は説明しますが、絡み合うことや金庫破りのことは説明の予定がありません。ご説明いただいた「調整」のことは金庫破りの記事に追記すればよいのだと思います。
> パラメーター調整で交わらずにすり抜ける可能性も意味しますから金庫破りや絡みを解く事が可能になります。
絡みを解けるというのはわかりますが、3次元空間で3次元の金庫破りもできてしまうわけですか??(それはあり得ないと思うのですが。)
3次元空間で線と線を交わるように1個のパラメーターを調整するというのは片方を1つの方向に平行移動して行けば交わるようにできるということ。3次元空間で点と線(z軸)を一致させる為にはxy座標を一致させる必要がありますから2個のパラメーター調整です。
逆にパラメーター調整で交わらずにすり抜ける可能性も意味しますから金庫破りや絡みを解く事が可能になります。
やはり「赤い布」のことをおっしゃっていたわけですか。
多様体やその次元について説明するのは、この記事のレベルをはるかに超えてしまうので、あくまで多様体を頭の隅に置きながら記事を書くことにしますね。
はい、そのことです。
曲線や曲面などは多様体ですので、
第8回目や第9回目で言っている「次元」とは
厳密には異なります。
多様体なのか、まっすぐな空間を考えているのかこだわる理由の一つとして、
線形空間の場合は線形部分空間同士(無限に伸びた平面と平面など)の共通部分は線形部分空間(無限に伸びた直線など)になりますが、
多様体の場合は多様体同士の共通部分は一般には多様体にならないので、
そうなると、「共通部分の『次元』とは?」と、
ちょっと考えなくてはならないことが出てきます。
>どうしましょうかねぇ。。。
個人的には、ここら辺は
あまり厳密にやりすぎるとキリがない気がします
(色々コメントをしておいてこう言うのは申し訳無いですが)。
厳密過ぎるとこの記事の趣旨から外れてくる気もしますので、
多少デリケートな部分には目を瞑ってると(書き手が)諒解しつつ、
「ものが絡まることの説明」をとねさん流に楽しく書いていくのが良いのではないでしょうか。
> 部分空間でない場合(例えば、原点を通らない直線)などを含めて議論する場合は、いわゆる「ねじれの関係」などが出てくるので、もう少し注意が必要です。
> この記事の場合は「交わる場合」を調べているので、平面や線は初めから原点を通るとしても問題は起きないと思います。どの文脈で議論をしてるのかを意識した方が良いかもしれません。
「ねじれの関係」になりそうなときは要注意なのですね。了解しました。
熱中して記事を書いているとつい「文脈」は意識の外に行きがちです。気をつけます。
> 前々回あたりの曲がった空間を考えてるときは、
> 多様体としての次元を考えていることになると思います。
この連載記事では空間で曲がったものを考えたことはありませんが、それはもしかすると「赤い布」のことですね!布の端を持ってゆっくり持ち上げたとき、それが多様体になっていることには気がついていませんでした。物体の次元について議論をしているわけですから厳密には多様体と線形空間の関係を示すことが必要ですね。直観的にはつながっていても論理的にはつながっていませんし。
でも記事は中学生、高校生にも理解していただきたいので、どうしましょうかねぇ。。。
次回の記事は多次元の球と球面、そしてそれらの次元の話なので、線形空間や多様体あたりをうまくからめて説明できればよいのですが。
アドバイスありがとうございます!
昼休みが終わってしまったので、また後でゆっくり考えてみますね。
少し補足しておくと、線形空間で考えてる場合は、
部分空間は必ず原点を通るので、0にして大丈夫です。
部分空間でない場合(例えば、原点を通らない直線)などを含めて議論する場合は、いわゆる「ねじれの関係」などが出てくるので、もう少し注意が必要です。
この記事の場合は「交わる場合」を調べているので、平面や線は初めから原点を通るとしても
問題は起きないと思います。
どの文脈で議論をしてるのかを意識した方が良いかもしれません。
あと、ここから先は蛇足ですが、
「次元」という言葉も、どの文脈で使ってるか
注意した方が良いでしょう。
例えば、この記事の場合は線形空間(あるいはアフィン空間)の次元の話ですが、
前々回あたりの曲がった空間を考えてるときは、
多様体としての次元を考えていることになると思います。
結局は多様体の場合も、
(変なのを考えなければ)同じ次元の接空間で近似して、線形代数の議論に落とし込んだりするので、
両者は関係が深いのですが、
一応、意識はしておいた方が良いでしょう。
> 共通部分の次元がマイナスなら0としてますが、これは点で交わる意味ですよ。
はい、少なくとも点では交わるだろうという想定で0にしておきましたが、まずいでしょうかね?
> 3次元空間での線と線の関係で最も一般的なのは全く交わらない場合です。点で交わるのは特殊です。
これは知っていました。ただし、この記事では全く交わらない場合は除外して考えるという前提で書いています。3次元空間で線と線が交わる場合のうち最も一般的なのはのは点で交わる場合ですね
> 共通部分の次元が-nとなったら、n個のパラメーターを特別な値に調整しないと交われません。
これは具体的にはどのようにすればよいのでしょうか?
3次元空間での線と線の関係で最も一般的なのは全く交わらない場合です。点で交わるのは特殊です。
共通部分の次元が-nとなったら、n個のパラメーターを特別な値に調整しないと交われません。