とりあえず、何度かミスった情報流しまくってましたが、今度こそオッケーと思われます。今思うと、最初のキバヤシの非直線部のあるなしはこの複数のPA区分を暗に示していたんだなーと感じます。
適当なPA値を持った機体での実測値と計算値が合ってるんだもの…もうキバヤシは呼ばせない!
Part1PA減衰距離とだいたいの時間
Part2AAの整波性能依存性
Part3AA多段ヒットについて
Part4AAのクリティカルヒットについて
Part5OBに設定された「アサルトアーマー攻撃力」依存性
Part6P-MARROWの効果
Part6.5キバヤシ1
Part7PA値12000~19310でのAA攻撃力
Part7.5キバヤシ2
Part8PA=8461~12000でのAA攻撃力補完
Part9AA攻撃力まとめ。
Part9.5総合AA攻撃力まとめの表。レギュ1.10のものなので現在役に立たない。
とりあえず、PA12000以上は式が合っていることは確定気味です。Part7.5で述べた通り、Part8では不十分と思われた12000以下のみを取り扱い、最後にPart9で攻撃力関係を全てまとめてアサルトアーマーの攻撃力計算分野はお開きにしようと思います。
データの取り方、単語の意味とかもろもろはPart7と完全に一緒です。とりあえずなんかやってるなってのがわかるだけでおk。
近似式のばらつき具合とか腑に落ちないところもあると思いますが、データの少なさに因るもので、最終結果はきちんと合ってるので大丈夫です。私もこんなに少なくていいのかなとか思うけれど合っちゃったからしょうがないよね。
傾きの生データ
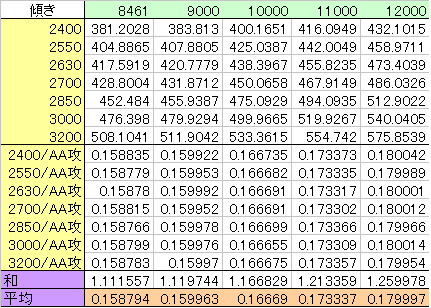
で、グラフ化すると、

です。
今回も近似式の切片を私の独断で補正しますが、前みたいにグラフ載せまくりのまどろっこしいことはしません。めんどいのでグラフは補正したヤツだけ載せますね。
まずデータの多い9000~12000から。こちらのデータの存在のおかげで9000以下をたった二つという少ないデータでも求められることになりました。
PA9000~12000の傾き近似式は、補正前は、
傾き= 0.0000066747×PA + 0.0999120869 R^2 = 0.9999931226
です。
ここで、切片=0.10に補正します。
補正後は、

です。
…なんか傾き部分の数字が666(ryっていい値じゃないですかコレ。2/3って感じだよね。Part7で出したPA=12000のときのPA12000~16000の方の計算式の傾きとも一致するし…。
ってことで、
PA=9000~12000で
AA攻撃力の傾き={2/3×10^(-5)×PA+0.10}×AA攻撃力/OB
で、残り。
PA8461~9000の傾き近似式は、補正前は
傾き= 0.00000216997×PA + 0.14043374422 でR^2 = 0.99999999997
です。
ここで、切片=0.14に補正します
補正後は、

です。
調子に乗って手ごろな0.14に補正してみたら傾きがなんか不安な値だよコレ…。ここで、先ほど求めたばかりのPA=9000~12000の傾きの計算式を利用します。PA=9000のとき、傾きは0.16と求められます。ってことは、式が変わるであろうPA=9000ジャストに8461~9000の傾き式を適用したときも0.16じゃね?と思うのは自然なことでしょう。
つまり、2219…とか出てる傾き-傾き部分がX=9000で0.02になればいい。ためしに、傾き-傾き係数=0.02/9000とやってみると…
0.0000022222…
ktkr いい感じ。9000~12000で2/3とか出たんだから2/9とか出てもおかしくないよね。
ってことで、
PA=8461~9000で
AA攻撃力の傾き={2/9×10^(-5)×PA+0.14}×AA攻撃力/OB
傾き部が求められました。次に切片部に移ります。切片部、特に切片-傾き部はデータが意味を為すとは思えない場面がありますが…。前から誤差のたまり場だったところで今更…
切片の生データ↓

グラフ化すると、以下のようになります。

上図の各PA値ごとの近似式の傾きと切片は以下に。

とりあえず安心な切片-切片部から行きます。
近似式は切片-切片部 = 0.24962295×PA + 3.15848357 R^2 = 0.99999278
これはPart7と一緒のパターンですね。
切片=0にします。

大体
AA攻撃力の切片-切片部=0.25×PA
って感じで傾向は変わらず。
さて、残るは切片-傾き部となりました。ここはデータは全くといってあてになりません、特に9000以下。ぶっちゃけExcelの計算式に適当な値代入しまくってガチッっとあてはまったもので最終的に済ませています、サーセンwww
PA=9000~12000で、
切片-傾き近似式=-0.0000064101×PA+0.1975225627 R^2= 0.9990879303
例のごとく、
切片=0.20にします。
補正後のグラフは、

ここで、切片-傾きグラフの傾き部の係数について。最初の方にあった傾きグラフの傾き部の係数を負にした感じが近いですよね。
ってことで、
PA=9000~12000で
AA攻撃力の切片-傾き部={2/3×10^(-5)×PA+0.20}×AA攻撃力/OB
と求められました。
あとはPA=8461~9000での切片-傾き部です。2つしかデータとってねー。マジめんどい。ここでいろいろとセコい技使います。
たった2点を結んだ式は、意味が凄まじく薄いですが…
切片-傾き近似式= -0.0000033585×PA + 0.1699612136
です。計算式にこれをもとにやってみましたが、これじゃ全然ダメです。

グラフ見ても分かるように、値域(yの値の範囲)が凄まじく狭いです。つまりデータ増やしても誤差考慮に四苦八苦しそうってこと。やってらんねー。
とりあえず切片値を近そうな0.17にやってみる?
0.17のときは、切片-傾き値 = -0.0000033629×PA + 0.1700000000 R^2 = 0.9999982518
確かにこの2点で言えば、ばらつきも少ないですが、傾き以前に実測値とは微妙に離れています。ここじゃないっぽい。
ここで一つの条件を適用させます。何気にさっきも使ってたりしますが、Part6.5でちょっと口走った一言です。
>総合AA攻撃力は、正の実数A~Eを用いると、
>総合AA攻撃力=(A×整波性能値+B)×AA攻撃力×(1,3,6,10,15,21)+{(-C×整波性能値+D)×AA攻撃力+E×整波性能値}×(1,2,3,4,5,6)
~~~~~~~~~
>個人的にデータの数値を見ているとA=Cではないかという疑惑がわきあがってくるものの、~
A=Cを適用させましょう。
つまりここでは2/9×10^(-5)です。
この値を固定しつつ、実測値に合う切片-傾きの切片値を探します。今までの傾向からそんなに複雑な数値ではないはずです。
切片値=0.16の場合だと実測値と合致しました。これに決めます。かなりのゴリ押しですね。しかしながらこのA=Cの根拠は、これまでのPA=9000~19310でのA,Cの値のデータに基づいており、これも一種のデータからの傾向読み取りとも言えます。
これで、レギュ1.10現在、PAフル時のPA=8461~12000のAA攻撃力計算式に必要な要素全てが求められました。
今回新たに求められた部分を含め、AA攻撃力関係はPart9に載せようと思います。
Part9、AA攻撃力まとめ
適当なPA値を持った機体での実測値と計算値が合ってるんだもの…もうキバヤシは呼ばせない!
Part1PA減衰距離とだいたいの時間
Part2AAの整波性能依存性
Part3AA多段ヒットについて
Part4AAのクリティカルヒットについて
Part5OBに設定された「アサルトアーマー攻撃力」依存性
Part6P-MARROWの効果
Part6.5キバヤシ1
Part7PA値12000~19310でのAA攻撃力
Part7.5キバヤシ2
Part8PA=8461~12000でのAA攻撃力補完
Part9AA攻撃力まとめ。
Part9.5総合AA攻撃力まとめの表。レギュ1.10のものなので現在役に立たない。
とりあえず、PA12000以上は式が合っていることは確定気味です。Part7.5で述べた通り、Part8では不十分と思われた12000以下のみを取り扱い、最後にPart9で攻撃力関係を全てまとめてアサルトアーマーの攻撃力計算分野はお開きにしようと思います。
データの取り方、単語の意味とかもろもろはPart7と完全に一緒です。とりあえずなんかやってるなってのがわかるだけでおk。
近似式のばらつき具合とか腑に落ちないところもあると思いますが、データの少なさに因るもので、最終結果はきちんと合ってるので大丈夫です。私もこんなに少なくていいのかなとか思うけれど合っちゃったからしょうがないよね。
傾きの生データ

で、グラフ化すると、

です。
今回も近似式の切片を私の独断で補正しますが、前みたいにグラフ載せまくりのまどろっこしいことはしません。めんどいのでグラフは補正したヤツだけ載せますね。
まずデータの多い9000~12000から。こちらのデータの存在のおかげで9000以下をたった二つという少ないデータでも求められることになりました。
PA9000~12000の傾き近似式は、補正前は、
傾き= 0.0000066747×PA + 0.0999120869 R^2 = 0.9999931226
です。
ここで、切片=0.10に補正します。
補正後は、

です。
…なんか傾き部分の数字が666(ryっていい値じゃないですかコレ。2/3って感じだよね。Part7で出したPA=12000のときのPA12000~16000の方の計算式の傾きとも一致するし…。
ってことで、
PA=9000~12000で
AA攻撃力の傾き={2/3×10^(-5)×PA+0.10}×AA攻撃力/OB
で、残り。
PA8461~9000の傾き近似式は、補正前は
傾き= 0.00000216997×PA + 0.14043374422 でR^2 = 0.99999999997
です。
ここで、切片=0.14に補正します
補正後は、

です。
調子に乗って手ごろな0.14に補正してみたら傾きがなんか不安な値だよコレ…。ここで、先ほど求めたばかりのPA=9000~12000の傾きの計算式を利用します。PA=9000のとき、傾きは0.16と求められます。ってことは、式が変わるであろうPA=9000ジャストに8461~9000の傾き式を適用したときも0.16じゃね?と思うのは自然なことでしょう。
つまり、2219…とか出てる傾き-傾き部分がX=9000で0.02になればいい。ためしに、傾き-傾き係数=0.02/9000とやってみると…
0.0000022222…
ktkr いい感じ。9000~12000で2/3とか出たんだから2/9とか出てもおかしくないよね。
ってことで、
PA=8461~9000で
AA攻撃力の傾き={2/9×10^(-5)×PA+0.14}×AA攻撃力/OB
傾き部が求められました。次に切片部に移ります。切片部、特に切片-傾き部はデータが意味を為すとは思えない場面がありますが…。前から誤差のたまり場だったところで今更…
切片の生データ↓

グラフ化すると、以下のようになります。

上図の各PA値ごとの近似式の傾きと切片は以下に。

とりあえず安心な切片-切片部から行きます。
近似式は切片-切片部 = 0.24962295×PA + 3.15848357 R^2 = 0.99999278
これはPart7と一緒のパターンですね。
切片=0にします。

大体
AA攻撃力の切片-切片部=0.25×PA
って感じで傾向は変わらず。
さて、残るは切片-傾き部となりました。ここはデータは全くといってあてになりません、特に9000以下。ぶっちゃけExcelの計算式に適当な値代入しまくってガチッっとあてはまったもので最終的に済ませています、サーセンwww
PA=9000~12000で、
切片-傾き近似式=-0.0000064101×PA+0.1975225627 R^2= 0.9990879303
例のごとく、
切片=0.20にします。
補正後のグラフは、

ここで、切片-傾きグラフの傾き部の係数について。最初の方にあった傾きグラフの傾き部の係数を負にした感じが近いですよね。
ってことで、
PA=9000~12000で
AA攻撃力の切片-傾き部={2/3×10^(-5)×PA+0.20}×AA攻撃力/OB
と求められました。
あとはPA=8461~9000での切片-傾き部です。2つしかデータとってねー。マジめんどい。ここでいろいろとセコい技使います。
たった2点を結んだ式は、意味が凄まじく薄いですが…
切片-傾き近似式= -0.0000033585×PA + 0.1699612136
です。計算式にこれをもとにやってみましたが、これじゃ全然ダメです。

グラフ見ても分かるように、値域(yの値の範囲)が凄まじく狭いです。つまりデータ増やしても誤差考慮に四苦八苦しそうってこと。やってらんねー。
とりあえず切片値を近そうな0.17にやってみる?
0.17のときは、切片-傾き値 = -0.0000033629×PA + 0.1700000000 R^2 = 0.9999982518
確かにこの2点で言えば、ばらつきも少ないですが、傾き以前に実測値とは微妙に離れています。ここじゃないっぽい。
ここで一つの条件を適用させます。何気にさっきも使ってたりしますが、Part6.5でちょっと口走った一言です。
>総合AA攻撃力は、正の実数A~Eを用いると、
>総合AA攻撃力=(A×整波性能値+B)×AA攻撃力×(1,3,6,10,15,21)+{(-C×整波性能値+D)×AA攻撃力+E×整波性能値}×(1,2,3,4,5,6)
~~~~~~~~~
>個人的にデータの数値を見ているとA=Cではないかという疑惑がわきあがってくるものの、~
A=Cを適用させましょう。
つまりここでは2/9×10^(-5)です。
この値を固定しつつ、実測値に合う切片-傾きの切片値を探します。今までの傾向からそんなに複雑な数値ではないはずです。
切片値=0.16の場合だと実測値と合致しました。これに決めます。かなりのゴリ押しですね。しかしながらこのA=Cの根拠は、これまでのPA=9000~19310でのA,Cの値のデータに基づいており、これも一種のデータからの傾向読み取りとも言えます。
これで、レギュ1.10現在、PAフル時のPA=8461~12000のAA攻撃力計算式に必要な要素全てが求められました。
今回新たに求められた部分を含め、AA攻撃力関係はPart9に載せようと思います。
Part9、AA攻撃力まとめ












※コメント投稿者のブログIDはブログ作成者のみに通知されます