8/31訂正:複数回答あるので条件文つけました。
<問題>
「とある小学校の担任をしている、秋子先生。
彼女のクラス、27人の児童は校内の合唱コンクールで
見事優勝を果たしました。ご褒美に、と校長先生から
頂いたのは、細長く切る前のカステラ丸ごと1個。
折角頂いたのですから、と昼食時に切り分けて食べることに
なりました。
ところが、みんな小学生ですからお菓子の大小だけでも
喧嘩沙汰に発展し . . . 本文を読む
問題
「ゴルフのマッチプレイがあります。概略は以下のとおり。
●2人or4人の2人組同士で対戦
●1ホールごとに勝敗を判断して、勝ちなら自分の勝ち数に+1。
負けなら相手の勝ち数+1。引き分けなら両者ポイント無し。
●最終的に、相手の勝ち数<自分の勝ち数、ならば勝利。
●自分から見て、自分がリードしている勝ち数
(「自分の勝ち数」-「相手の勝ち数」)が
残り . . . 本文を読む
(問題)
「ある自然数を要素とする無限集合A={a(1), a(2), ... }があります。
この中から、1つの要素a(k)と1つの有限な部分集合Atを抜き出します。ただし、
Atは空集合では無いとします。At={a(t1), a(t2), ..., a(tp)}とします。
このとき、Atの全要素の総和St=Σa(ti)=a(t1)+a(t2)+...+a(tp)は、
a(k)の1/2以下とな . . . 本文を読む
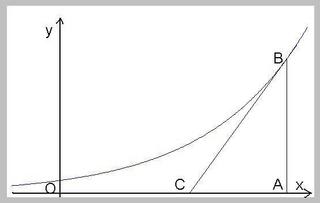
問題:
ある曲線Fが方眼用紙上にあります。
この曲線とy軸との交点、つまり切片は1です。
x軸上のある点Aから垂線を引き、Fとの交点を
Bとします。点B上でのFの接線を引いたとき、
x軸との交点をCとします。
もし、任意の点AについてAC=1という条件が
成り立つとした場合、曲線Fはどんな式で表現
できるでしょうか? . . . 本文を読む
ごめんなさい!!
用意した解答が間違いだったようです orz...
反例: {x,y,z}={8,15,17},...etc.
問題
X,Y,Zを以下の条件を満たす自然数とします。
1、 X^2 + Y^2 = Z^2
2、 X < Y < Z
3、 3つのうち2つは奇数で1つは偶数
いわゆるピタゴラスの定理です。
例えば、{X,Y,Z}={3,4, . . . 本文を読む
自由課題:
家電量販店などの、ポイント還元システム
について、あなたは次のA,Bのどちらの傾向が
強いか考察せよ。
A: ポイントは溜めて大きな買い物の際に使用
B: ポイントは小まめに使用してあまり残さない
また、客、店のそれぞれの立場から、AとBの
どちらが良いのかも考察せよ。
(注)いわゆる数学的な問題ではないので、
これといって明確な解答は不要。
. . . 本文を読む
絶対に試験に出ない数学の問題のネタが出ないので
しばらく更新できずにいたら、某所で「最近更新が無い」と
言っていた人がいると聞き頭を捻ってみる。
。。。が、面白いものがない。 orz...
なので、自分で問題提供するのはお休みして、他の方の
作成された問題の中から、自分がとても感動したものを
ここで紹介するということにした。いや、させて下さい。
●問題 (from 数学オリンピック198 . . . 本文を読む
今年も、絶対に試験に出ない問題をよろしくお願いします。
(問題)
次の例のように、1/aの分数を複数の1/?型の分数に
分解することを考えます。
例) 1/2 = 1/6 + 1/3
次の等式のa,b,cに当てはまる値をそれぞれ
求めなさい。ただし、a,b,cは全て自然数
(1以上の整数)で、a>b>cを満たす
という条件でaが最小の組とします。
1) 1/20 . . . 本文を読む
パンヤ公式BBSで確率統計の話があったのだが、
200個じゃサンプル足りないという根拠はどこに?という
感じがした。感覚的には確かにそうなんだが。
で、高校の教科書「確率・統計」ってのを借りてきて
(数学Cとかじゃない時点で持ち主の年齢が判るな)
検定の部分を読み直してみた。
で、結論として、
仮説「ラキパン補助剤は、1/3で失敗する」
に対して、サンプル200個の結果で検定を行うとする。 . . . 本文を読む
とうとう、数学ネタまで「パンヤ」から引用することになるとは。
※パンヤの用語が混じりますので、知らない方は下に用語解説してます。
問題:
「ケンとエリカは、まだパンヤ始めたばっかりのルーキーさんです。
頑張って4級大会に臨んだものの、結果は。。。
そこで、同一のコースを一杯対戦をして特訓することにしました。
ケンは、ある程度長いホール数を回りたいと9Hランダムの
対戦を沢山繰り返しまし . . . 本文を読む