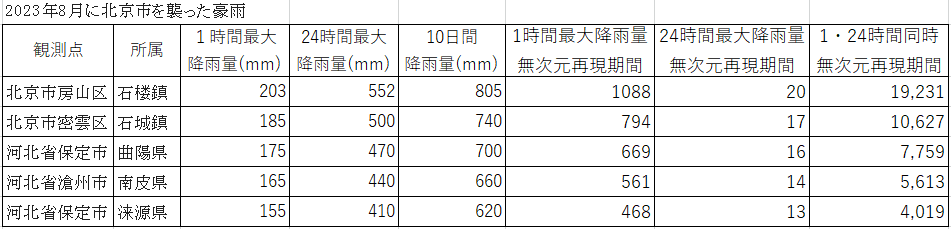
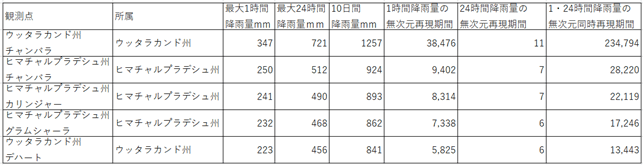
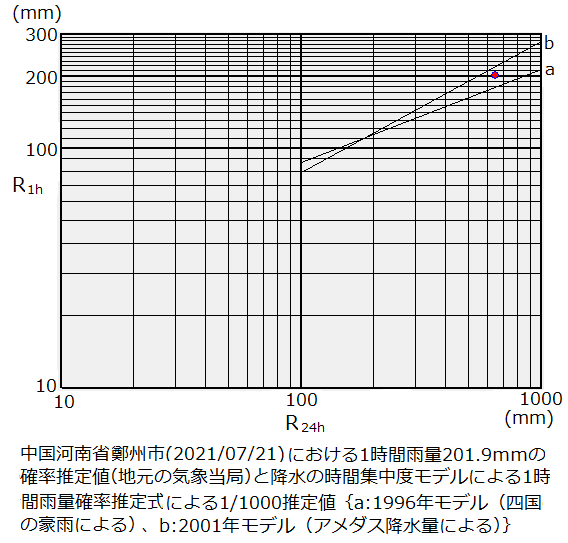
Conditional precipitation probability model for a given time interval

Conditional precipitation probability model for a given time interval

Hydrostatistics is a discipline that aims to determine the extreme values of unit-time rainfall using probability statistics and apply them to water resource planning and the design and management of hydraulic structures. Conventional hydrostatistics directly analyzes the extreme values of unit-time rainfall, assuming that unit-time rainfall is an independent random variable. However, this assumption is only partially valid, and experiencing unprecedented extreme values can lead to damages beyond expectations.

One possible explanation for the emergence of unprecedented extreme values is the presumed influence of global warming. Therefore, there is a need to develop new probabilistic models for studying the extreme values of unit-time rainfall.

Interestingly, such new probabilistic models already exist in the form of analytical models known as the Depth-Duration (DD) and Depth-Area (DA) equations. Notable examples of the DD equation include the Sherman equation, and the Horton equation is a well-known example of the DA equation.

 Sherman式: rt = a / t^c, where, rt is average rainfall intensity at time t, and a and c are coefficients.

 Horton式: PA = P0 * exp(-k * A^n), where, PA is average rainfall over area A, P0 is maximum rainfall within area A, k and n are coefficients.

Analysis of the DD equation is typically conducted on log-log paper. The coefficient c is known as the shape parameter. This designation stems from the observation that on log-log paper, the mean rainfall intensity over time t exhibits an approximately linear distribution with respect to the time axis.

However, as long as the coefficient c is referred to as the shape parameter, the DD equation does not qualify as a probabilistic model. To transform the DD equation into a probabilistic model, dimensionless unit time 1 and dimensionless representative time T are introduced. The rainfall intensity per unit time is represented by r1, and the average rainfall intensity over time T is denoted by rT. The DD equation is expressed as the ratio between these two quantities.

 Log(r1/rT)=logT^c

Consider a scenario where T units of time receive RT mm of rainfall. What is the maximum possible rainfall in millimeters per unit time? The maximum value is RT/1, and the minimum value is RT/T. In the former case, the coefficient c is equal to 1, while in the latter case, c is equal to 0. Consequently, the coefficient c is distributed within the range [0, 1]. However, if RT is sufficiently large, the distribution becomes (0, 1). This implies that the coefficient c can be transformed into a random variable.

By incorporating dimensionless unit time and dimensionless representative time into the solution of the DD equation, the DD equation can be transformed into a probabilistic model. However, while the coefficient c is determined by a random variable, it is also dependent on RT over time T. Therefore, unit-time rainfall is not an independent random variable. I refer to the coefficient c as the "temporal concentration degree of rainfall."

2023年8月に中国北京市を襲った豪雨の無次元再現期間

2023年8月に中国北京市を襲った豪雨について、GoogleのBardで検索した結果に基づいて、無次元再現期間を計算しました。

　質問は、2023年8月に北京市は洪水による大災害に見舞われた。この洪水の原因となった豪雨域の5つの観測点（所属）をあげてください。その各観測点の最大１時間降雨量、最大24時間降雨量、10日間降雨量を教えてください。

回答案1（但し表はexcelで書き換え、無次元再現期間を追加しました。）

「2023年8月に北京市を襲った豪雨の原因となった豪雨域の5つの観測点は、以下のとおりです。

これらの観測点では、7月31日から8月10日までの10日間で、平均して1日あたり70mm以上の雨が降りました。そのうち、8月1日には、北京市房山区 石楼鎮で最大1時間降雨量203mm、最大24時間降雨量552mmという記録的な降雨量を記録しました。

この豪雨により、北京市と河北省では、洪水や山崩れなどの被害が相次ぎました。北京市では、死者・行方不明者が合わせて51人に上り、129万人近くが被災しました。」

　北京市密雲区の1時間降雨量の無次元再現期間は1088となっており、7月の河北省の豪雨と同程度か上回るほどの豪雨であったと思われます。

2023年8月のインドにおける豪雨の無次元再現期間

最近、温暖化の影響であろうか、中国やインドなど世界のあちこちで異常な豪雨が発生しています。2023年8月に発生したインドヒマチャルプデシュ州・ウッタラカンド州の豪雨についてGoogleのBardで検索した回答案に挙げられた値に基づいて確率計算を試みます。

　検索における質問文は、「2023年にインドで洪水被害をもたらした豪雨域の5つの観測点とその所属をあげ、最大1時間降雨量、最大24時間降雨量、10日間降雨量を教えてください。」としました。以下はその回答案1です（表の値をexcelに移転、無次元再現期間を追加）。

回答案1

「2023年にインドで洪水被害をもたらした豪雨域の5つの観測点とその所属、最大1時間降雨量、最大24時間降雨量、10日間降雨量は以下のとおりです。

これらの観測点は、いずれもインド北部のヒマチャルプラデシュ州とウッタラカンド州に位置しています。最大1時間降雨量は、ウッタラカンド州のチャンバで347mmと、最も高く、最大24時間降雨量は、ヒマチャルプラデシュ州のチャンバラで721mmと、最も高くなっています。10日間降雨量は、いずれの観測点でも1,000mmを超え、甚大な被害をもたらしました。

なお、これらのデータは、インド気象局の観測データに基づいています。」

　

　回答案1の最大1時間降雨量の値は過大であるように思いますが、インド気象局の観測データとしているのでそのまま利用して計算します。ただし、私の計算式の適用外になるので、参考までに計算したという程度です。

　ウッタラカンド州チャンバラの最大1時間降雨量の無次元再現期間は38,476、24時間降雨量の再現期間は11、両者の同時再現期間は234,794となり、信じられないような値です。確認が必要です。

　

　この降雨量は異常すぎるので、回答案2の値も見てみます。

回答案2

「2023年にインドで洪水被害をもたらした豪雨域の5つの観測点は、以下のとおりです。

これらの観測点のうち、最大1時間降雨量が最も多かったのはシムラで、165mmでした。最大24時間降雨量が最も多かったのはデリー(?シムラ）で、227mm(?297)でした。10日間降雨量が最も多かったのはシムラで、1,187mmでした。

この豪雨は、インド北部のヒマチャルプラデシュ州とウッタラカンド州で発生しました。この地域は、急峻な地形と、夏季のモンスーンの影響を受けることから、洪水や土砂崩れの被害が頻発しています。」

　回答案2の値は日本でも観測される値です。

　各観測点の1時間降雨量の無次元再現期間は1000を超えています。24時間降雨量の無次元再現期間が1となっているのは10日間降雨量に比べて、値が小さいからであると思われます。

実用水文統計解析の係数

中国河南省鄭州市における2021年7月豪雨

　2021/07/22の高知新聞に、『中国豪雨120万人被災』の見出しで、【北京、上海共同】中国河南省鄭州市の豪雨災害が報じられた。『地元の気象当局は「千年に一度」の激しい雨だと指摘した。』。中略『鄭州市で20日午後４時から５時までの１時間に201.9ｍｍの雨が降った。』。
　また、8月２5日の現代ビジネスに『鄭州市では7月16日から連日豪雨が降り続いた。鄭州市の年間平均降雨量は640.8ミリメートル。だが、『7月17日20時から7月20日20時までのわずか3日間で降雨量は617.1ミリメートルに達し、さらに7月20日早朝4時から21日早朝4時までのたった24時間で降雨量は645.6ミリメートルに達し、わずか1日で年間雨量を上回ったことになる。』と報じた。（https://gendai.ismedia.jp/articles/-/86551?page=2、2021/10/11）　
　結局、７月16日から21日までの総雨量は1262.7ｍｍ超、最大24時間雨量は645.6ｍｍ、最大1時間雨量201.9ｍｍとなる。
　日本の過去最大1時間雨量は1982年長崎豪雨（長与町）で観測された187ｍｍ、24時間雨量は541ｍｍであり、降水の時間集中度モデルによる推定式を用いて超過確率を約1/1584と推定した。
　『地元の気象当局は「千年に一度」』と推定しているが、推定の方法は不明である（赤丸）。そこで降水の時間集中度モデルによる確率推定式による推定値と比較する。推定式は総雨量に従属するので厳密な比較はできないが、過去に作成した推定式aおよびbの中間にあり、妥当な推定であると思われる。