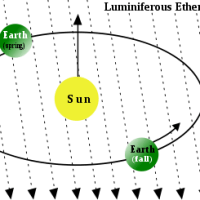
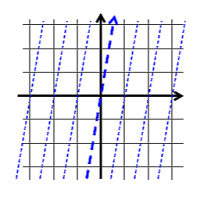
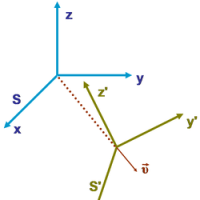
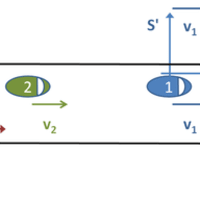
しかし、物が動いているのを計算するにしても、
土台となる基準が必要になります。
この基準に、デカルト座標(直交座標系)があります。
(2次元)
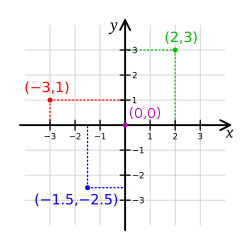

デカルト座標の優れている点は、
数式の各点と、座標が一対一対応になっていて
数式(解)があれば、それは座標に対応しており、
座標の諸点は、数式(解)に対応していることです。
(1次元)

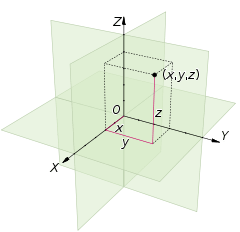
(3次元)

(回転体)
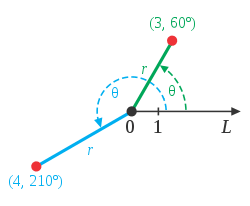
これらの座標は、ユークリッド幾何学が基になっています。
ユークリッド幾何学の特徴は、
1次元であれば、直線
2次元であれば、2本の直交座標
3次元であれば、3本の直交座標
から成立していることです。
The Cartesian Coordinate System an Introduction
直交座標系 - Wikipedia
数学における直交座標系(ちょっこうざひょうけい、rectangular coordinate system, orthogonal coordinate system)とは、互いに直交している座標軸を指定することによってさだまる座標系のことである。平面上の直交座標系ではそれぞれの点に対して一意に定まる2つの実数の組によって点の位置が指定される。同様にして空間上の直交座標系では3つの実数の組によって座標が与えられる。1637年に発表された『方法序説』において平面上の座標の概念を確立したルネ・デカルトの名を採ってデカルト座標系 (Cartesian coordinate system) とも呼ぶ。
Video for Lesson 22: Names of Three-Dimensional Figures
ユークリッド幾何学 - Wikipedia
ユークリッド幾何学(ユークリッドきかがく、英語:Euclidean geometry)は、幾何学体系の一つであり、古代エジプトのギリシア系哲学者エウクレイデスの著書『原論』に由来する。古代エジプトや古代ギリシャなどでは盛んに幾何学が研究されていた。
エウクレイデスはその成果を『原論』の1~4巻において体系化した。その手法は、1.まず、点や線などの基礎的な概念に対する定義を与える。2.次に、一連の公理を述べ、公理系を確立する。3.そして、それらの上に500あまりの定理を証明する。という現代数学に近い形式をとっており、完成されたものであったので、それ以降の多くの幾何学者はこの体系の上に研究を進めた。ヨーロッパでは重要な教養の一つと考えられていたものである。こうして基礎づけられ発展した体系は、エウクレイデス(英名:Euclid ユークリッド)に因んでユークリッド幾何学と呼ばれるようになった。
土台となる基準が必要になります。
この基準に、デカルト座標(直交座標系)があります。
(2次元)


デカルト座標の優れている点は、
数式の各点と、座標が一対一対応になっていて

数式(解)があれば、それは座標に対応しており、
座標の諸点は、数式(解)に対応していることです。
(1次元)

(3次元)

(回転体)

これらの座標は、ユークリッド幾何学が基になっています。
ユークリッド幾何学の特徴は、
1次元であれば、直線
2次元であれば、2本の直交座標
3次元であれば、3本の直交座標
から成立していることです。

The Cartesian Coordinate System an Introduction
直交座標系 - Wikipedia
数学における直交座標系(ちょっこうざひょうけい、rectangular coordinate system, orthogonal coordinate system)とは、互いに直交している座標軸を指定することによってさだまる座標系のことである。平面上の直交座標系ではそれぞれの点に対して一意に定まる2つの実数の組によって点の位置が指定される。同様にして空間上の直交座標系では3つの実数の組によって座標が与えられる。1637年に発表された『方法序説』において平面上の座標の概念を確立したルネ・デカルトの名を採ってデカルト座標系 (Cartesian coordinate system) とも呼ぶ。
Video for Lesson 22: Names of Three-Dimensional Figures
ユークリッド幾何学 - Wikipedia
ユークリッド幾何学(ユークリッドきかがく、英語:Euclidean geometry)は、幾何学体系の一つであり、古代エジプトのギリシア系哲学者エウクレイデスの著書『原論』に由来する。古代エジプトや古代ギリシャなどでは盛んに幾何学が研究されていた。
エウクレイデスはその成果を『原論』の1~4巻において体系化した。その手法は、1.まず、点や線などの基礎的な概念に対する定義を与える。2.次に、一連の公理を述べ、公理系を確立する。3.そして、それらの上に500あまりの定理を証明する。という現代数学に近い形式をとっており、完成されたものであったので、それ以降の多くの幾何学者はこの体系の上に研究を進めた。ヨーロッパでは重要な教養の一つと考えられていたものである。こうして基礎づけられ発展した体系は、エウクレイデス(英名:Euclid ユークリッド)に因んでユークリッド幾何学と呼ばれるようになった。