観察する人間の座標系によって、
見かけが異なる運動形式になるために、
それらをお互いに換算したり、変換したりする必要があります。

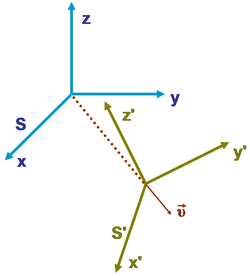
結局、それぞれが独立した慣性系(視点)が、無数にあるということです。
※ガリレイ変換
もし、室内で読書する人の運動状態を「静止している」としても、
本当は、車の中にいるかもしれないし、
または、ただの外の映像が部屋に流れていて
部屋が(動いていないのに)動いてるように見えるのかもしれません。
これらは、評価速度が全く変わってきます。
スピードが違う二台の車は、
それぞれお互いを違うスピードで動いていると見なします。
さらに、地上で静止している人からは、また2台とも違う速度に観測します。
そして対向車は、接近速度が加算されます。
では、静止座標というのは、どこにあるのでしょう?
もし人が、部屋で、車や電車にも乗らず、飛行にも乗らず、
本当に、地面に対して動かないという意味で、
椅子に座ってじっとしていながら、
同時に毎時900マイル(毎時1.450キロ)で移動する
なんてことは可能でしょうか?
答えは、「可能」です。
ある人が、机にじっと座り、
机は、家に対して固定していて、
家は大地(地球)に固定していています。
その地球は、しかし、自転しています。
一日に一回転しています。

もし赤道(Equator)下であれば、
周囲は25000マイル(40.075キロ)あるので、
時速約1000マイル(毎時約1.600キロ)です。
アメリカのアトランタだと、時速約860マイルになります。
でも、もし北極や南極で、地軸の真上にいたら、どうでしょうか?
完全な静止座標でしょうか?
ところが、地球は太陽の周りを好転していて、
そのスピードは、秒速約16マイル(秒速25キロ)です。
さらに、太陽系は、銀河系の中心を巡っています。
銀河系は、どこかに対して動いています。
ということで、この宇宙で、
計算に便利な「完全な静止座標」というものはありません。
Cognifront.Relative-Motion
ガリレイ変換 - Wikipedia
ガリレイ変換(ガリレイへんかん、英語:Galilean transformation)とはある慣性系における物理現象の記述を別の慣性系での記述に変換するための座標変換の方法の一つである。相対論的効果を考慮していないので厳密には正しくないが、光速に比べて十分遅い速度のみを扱う場合は近似的に成り立つと見なせ、特に日常生活で接する程度の速度では極めて厳密に成り立つ。
ガリレイ変換(ガリレイへんかん、英語:Galilean transformation)とはある慣性系における物理現象の記述を別の慣性系での記述に変換するための座標変換の方法の一つである。相対論的効果を考慮していないので厳密には正しくないが、光速に比べて十分遅い速度のみを扱う場合は近似的に成り立つと見なせ、特に日常生活で接する程度の速度では極めて厳密に成り立つ。
Physical Science 1.3a - Reference Frames
慣性系 - Wikipedia
慣性系(かんせいけい、ガリレイ系とも、英語:inertial frame of reference)は、慣性の法則(運動の第1法則)が成立する座標系である。太陽系の重心に原点を取り、恒星系に対して回転しない座標系は慣性系に近いことが現在分かっている。慣性系によって物体の運動状態を記述するとき、その物体は外力を受けない限り、等速直線運動を行う。
見かけが異なる運動形式になるために、
それらをお互いに換算したり、変換したりする必要があります。


結局、それぞれが独立した慣性系(視点)が、無数にあるということです。
※ガリレイ変換

もし、室内で読書する人の運動状態を「静止している」としても、
本当は、車の中にいるかもしれないし、
または、ただの外の映像が部屋に流れていて
部屋が(動いていないのに)動いてるように見えるのかもしれません。
これらは、評価速度が全く変わってきます。
スピードが違う二台の車は、
それぞれお互いを違うスピードで動いていると見なします。
さらに、地上で静止している人からは、また2台とも違う速度に観測します。
そして対向車は、接近速度が加算されます。
では、静止座標というのは、どこにあるのでしょう?
もし人が、部屋で、車や電車にも乗らず、飛行にも乗らず、
本当に、地面に対して動かないという意味で、
椅子に座ってじっとしていながら、
同時に毎時900マイル(毎時1.450キロ)で移動する
なんてことは可能でしょうか?
答えは、「可能」です。
ある人が、机にじっと座り、
机は、家に対して固定していて、
家は大地(地球)に固定していています。
その地球は、しかし、自転しています。
一日に一回転しています。

もし赤道(Equator)下であれば、
周囲は25000マイル(40.075キロ)あるので、
時速約1000マイル(毎時約1.600キロ)です。
アメリカのアトランタだと、時速約860マイルになります。
でも、もし北極や南極で、地軸の真上にいたら、どうでしょうか?
完全な静止座標でしょうか?
ところが、地球は太陽の周りを好転していて、
そのスピードは、秒速約16マイル(秒速25キロ)です。
さらに、太陽系は、銀河系の中心を巡っています。
銀河系は、どこかに対して動いています。
ということで、この宇宙で、
計算に便利な「完全な静止座標」というものはありません。
Cognifront.Relative-Motion
ガリレイ変換 - Wikipedia
ガリレイ変換(ガリレイへんかん、英語:Galilean transformation)とはある慣性系における物理現象の記述を別の慣性系での記述に変換するための座標変換の方法の一つである。相対論的効果を考慮していないので厳密には正しくないが、光速に比べて十分遅い速度のみを扱う場合は近似的に成り立つと見なせ、特に日常生活で接する程度の速度では極めて厳密に成り立つ。
ガリレイ変換(ガリレイへんかん、英語:Galilean transformation)とはある慣性系における物理現象の記述を別の慣性系での記述に変換するための座標変換の方法の一つである。相対論的効果を考慮していないので厳密には正しくないが、光速に比べて十分遅い速度のみを扱う場合は近似的に成り立つと見なせ、特に日常生活で接する程度の速度では極めて厳密に成り立つ。
Physical Science 1.3a - Reference Frames
慣性系 - Wikipedia
慣性系(かんせいけい、ガリレイ系とも、英語:inertial frame of reference)は、慣性の法則(運動の第1法則)が成立する座標系である。太陽系の重心に原点を取り、恒星系に対して回転しない座標系は慣性系に近いことが現在分かっている。慣性系によって物体の運動状態を記述するとき、その物体は外力を受けない限り、等速直線運動を行う。









