
「固体物理の基礎 下・1 固体フォノンの諸問題: アシュクロフト、マーミン」
内容紹介:
学部生にも大学院生にも使えるよう工夫され、内容の取捨選択がしやすく、種々の目的、異なる水準でもうまく使い分けられる。固体物理学の現象の記述と理論的解析による統一という著者の目標は完全に達成されている。1981年刊行、282ページ。
著者について:
ニール・W・アシュクロフト(ウィキペディア、経歴詳細)
イギリスの物理学者(固体物理学)、1938年生。1958年ニュージーランド大学卒業。学位は1964年ケンブリッジ大学。シカゴ大学およびコーネル大学で博士研究員、1975年教授。1990年にHorace White Professor of Physics。2006年名誉教授。
デヴィッド・マーミン(ウィキペディア、ホームページ)
コーネル大学名誉教授(物理学)。米国物理学会のリリエンフェルト賞および米国物理教育学会のクロプステッグ賞を受賞。米国科学アカデミー、米国芸術科学アカデミーの会員。この数十年の間に、量子論の基礎的な問題に関する多くの著作を執筆しており、科学の啓蒙に関する明瞭さと機知には定評がある。
訳者について:
松原武生(まつばらたけお)
1921-2014 昭和後期-平成時代の理論物理学者。
大正10年4月3日生まれ。北大教授をへて昭和30年京大教授となる。61年岡山理大教授。誘電体、超伝導、超流動などを研究。「温度グリーン関数」の概念を提案した。36年仁科記念賞。日本物理学会会長をつとめた。平成26年12月15日死去。93歳。大阪府出身。大阪帝大卒。著作に「超流動と超伝導」「固体物理学」など。
町田一成(まちだかずしげ)
1968年東京教育大学理学部卒業。1973年同上理学研究科博士課程修了。京都大学理学部助手、岡山大学理学部助教授、教授を経て、岡山大学大学院自然科学研究科教授。
理数系書籍のレビュー記事は本書で280冊目。
3冊目に入ってからますますハードな勉強になってきた。固体の種類を分類した後、それぞれについて比熱や熱膨張率、熱伝導、電気抵抗、固体を伝わる音の速度など物性を計算する手順を解説する。
固体を伝わる熱は原子の格子振動による現象であること、その振動はフォノンや伝導電子によることは「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」という記事で大ざっぱに説明したことがあるが、本書ではそのことを固体物性の立場から詳細に解説、計算している。
結晶の静止格子模型がどのように破綻するか、そして静止模型から調和振動模型を採用して古典的、そして量子論的アプローチへと発展させる。それでもなお実験とのずれが生じるケースに対しては非調和振動模型を適用し、計算はますます複雑になっていく。
物理現象の中には調和振動理論では説明できないものが多数あり、それはイオン相互作用エネルギーをその平衡値の周りに展開したときの高次の項を無視したことによるものである。このような非調和項の存在が要求される現象には次のようなものがある。
- 調和結晶の量子論は比熱が高温でデュロン・プティの古典法則に従うことを予言するが、実際はそうならない。
- 非弾性的な中性子散乱の断面積は1-フォノン過程を支配する保存則によって許されたエネルギーのところで鋭いピークをもつが、実際に観測されるピークは相当明確なピークであっても観測可能な幅をもっている。1-フォノン・ピークの幅は、イオン相互作用エネルギーの非調和部分の強さのひとつの直接測定量である。
- 熱膨張は非調和項の存在で説明される。厳密に調和的な結晶では平衡状態の大きさは温度によらない。また弾性定数が体積にも温度にもよらないこと、断熱的と等温的とで弾性定数が等しくないことも非調和項によるものである。
- 絶縁固体の熱伝導度はイオン相互作用エネルギーの非調和項によってのみ有限におさえられる。厳密的に調和的な結晶は無限に大きい熱伝導度をもつと予測する。
固体の分類に従ったそれぞれのケースについて詳しく解説しているという意味ではとても優れた教科書だが、そのぶん記述がボリュームが増すことで「木を見て森を見ず。」の状況に陥りやすい。
僕はこの分野の専門家には絶対になれないと確信した1冊になった。後で思い出せるように、要点だけをこの記事にまとめておこう。
章立ては次のとおりだ。
下・1:固体フォノンの諸問題
第19章:固体の分類
第20章:凝集エネルギー
第21章:静止格子模型の破綻
第22章:調和結晶の古典論
第23章:調和結晶の量子論
第24章:フォノン分散関係の測定
第25章:結晶の非調和効果
第26章:金属中のフォノン
第27章:絶縁体の誘電的性質
付録
本書で特に重要なキーワードを解説しているページと短い説明を書いておこう。
分子性結晶(希ガス結晶):
典型的な例は希ガス固体つまりネオン、アルゴン、クリプトンとキセノンである。それらの原子状態は完全に占有された電子殻となっている。これは非常に安定した配置であり、固体になってもほんの少ししか変わらない。バンド構造という点から希ガスは強く束縛された固体の典型のよい例である。つまり電子密度はイオン芯の間ではほとんどなく、電子はすべてその属したイオンの近くに局在したままである。
注意:分子性結晶という表現は、分子間力以外の結合様式も入り込んだ場合用いる用語である。(分子結晶という表現との違いに注意。)
共有結合結晶:
共有結合によって形成される結晶のこと。一つの結晶粒で一つの分子(巨大分子)を形成しているため、化学式で表す際は形成される元素とその比率により表される。共有結合結晶とも呼ばれる。ダイヤモンドなどのように、共有結晶の中で各原子どうしは強い結合を形成する場合があり、その結果、融点が高かったり硬い性質を持つ場合がある。通常、電気伝導性はほとんどない。の他、ケイ素(シリコン)、二酸化ケイ素などが共有結晶を作る。
電子の空間分布としては、部分的にしか占有されていないバンドを持たない電子分布である。そのため結晶の電子はイオン芯の近くに鋭く局在している必要もない。また単純金属のように中間領域で、電子分布はほとんど一様ということでもない。
イオン結合結晶:
イオン結合によって形成される結晶のこと。この結晶は、異符号のイオン同士が隣り合いクーロン力によって結び付けられ固定されることでできる。イオン結合は強い結合なのでイオン結晶は融点が高く、硬い性質を持つ場合が多いが、脆くて壊れやすい性質も持つ。この性質を劈開という。これは、外力が加わると同符号のイオン同士が接近して、互いに反発しあうためである。通常、固体では電気伝導性はない(超イオン伝導体は例外)が、融点を超えて液体となった場合や溶質として水などに溶かすと電気を導く。これは、液体や水溶液になることで電荷を持ったイオンが移動できるようになるためである。水溶液中では電離して水和イオンとして存在する。このように水中で電離する物質を電解質という。
イオン結晶の最も素朴なモデルでは、すべてのイオンを貫通できない荷電球として扱う。結晶は正と負の荷電球の間の静電引力によって結合しており、球は貫通できないので結晶が壊れることはない。このように貫通できないのはパウリの排他原理やイオンの電子配置が安定な閉殻であることの結果である。二つのイオンを近づけるとその電子電荷分布は重なり始める。そのとき排他原理によって、各イオンの近くに他のイオンによって作られた過剰な電荷は占有されていない状態に収容されることになる。しかし正と負のイオンの電子配置は安定な閉殻である。これは占有状態と最低非占有状態の間に大きなエネルギー・ギャップが存在することを意味する。その結果、電荷分布を無理に重なり合わせるのには非常に多くのエネルギーを必要とする。つまりイオンを近づけて電子電荷分布が互いに重なり合うと強い反発力がそのイオン間に働く。
水素結合結晶(分子結晶):
結晶のうち、分子同士の親和力として主に水素結合を利用して形成されているもののこと。水素結合性結晶とも呼ばれる。もっとも身近で代表的な水素結合結晶は氷である。通常の水素結合はファン・デル・ワールス力よりも強いため、同程度の分子量の化合物で比べた場合、水素結合結晶のほうがファンデルワールス結晶よりも格子エネルギーが大きい、すなわち融点が高いことが多い。
ファンデルワールス結晶(分子結晶):
分子間力の一種であるファンデルワールス力によって形成される結晶のこと。ファンデルワールス力による結合は弱いので、分子結晶の格子エネルギーは弱く、融点が低かったり、柔らかかったり、昇華性を持ったりする場合が多い。主な例として、ドライアイスやナフタレン、非極性の高分子化合物などがあげられる。
一般に、静電相互作用や水素結合などのより強い分子間相互作用がはたらかないような分子が結晶となる場合にとる形式である。
金属:
金属を原子の化学結合で定義する場合、特有の金属結合で説明される。これは、カチオン化した金属元素が規則正しく並び、その間を自由電子が動き回りながら、これらがクーロン力で結びついている結合を指し、常温下でこのような結合状態にある物質を金属と定義している。原子の配列は、ほとんどの場合、面心立方格子構造 (fcc)、体心立方格子構造 (bcc)、六方最密充填構造 (hcp) のいずれかを取り、元素の種類や同じ元素でも状態によってそれぞれの構造となる。この構造はそれぞれ原子充填率が異なり、金属の塑性変形に影響を与える。
金属の定義や分類はウィキペディアの項目を参照していただきたい。
周期表をIV族から左にいくと金属の族に行きつく。共有結合が拡がり、すき間の領域全体にも電子密度が認められ、k-空間(波数ベクトル空間)ではバンドが重なり合う。金属結晶の重要な例はI族のアルカリ金属である。それらの金属は多くの目的に対してはゾンマーフェルトの自由電子模型よって正確に記述できる。この模型では価電子はイオン芯から完全に分離しており、ほとんど一様な気体を形成する。さらに一般的なことであるが、金属においてさえ共有結合や分子性結合の性質がみられる。とくに貴金属では占有されている原子のd殻はあまりきつく束縛されておらず、その結果金属中ではかなり歪んでいる。
凝集エネルギー:
液体や固体など、凝集状態にある原子またはイオンを、互いに引き離してばらばらにするために必要なエネルギー。
マールディング定数:
イオン結晶において、静電気的なポテンシャルエネルギーを表す定数をマーデルング定数と呼び、結晶構造の種類により決まる定数である。(ウィキペディアの「マールディングエネルギー」を参照。)
ヴィーデマン・フランツ法則:
金属の熱伝導率Kと、電気伝導率σの比が温度に比例することを示したものである。金属の場合、熱伝導と電気伝導の両方の大部分を自由電子が担うので、この関係が成り立っている。
デュロン・プティの法則:
固体元素の定積モル比熱 C_V が常温付近(デバイ温度より大きい領域)ではどれもほとんど等しく、 C_V = 3R = 3N_Ak_B ( = 5.96 cal/mol・K、 R は気体定数、 N_A , k_B はそれぞれアヴォガドロ定数とボルツマン定数)であるという法則。エネルギー等配分の法則やデバイ模型から導出できる。
デバイ模型:
熱力学と固体物理学において、固体におけるフォノンの比熱(熱容量)への寄与を推定する手法である。デバイ模型では、原子の熱による格子振動を箱の中のフォノンとして扱う。デバイ模型は低温における比熱のT^3に比例する温度依存性を正しく予言する。また比熱の高温におけるデュロン=プティの法則に従う振る舞いも正しく説明することができる。しかし格子振動を単純化して扱っているため、中間的な温度における正確性には弱点がある。
アインシュタイン模型:
熱力学と固体物理学において、固体を相互作用のない量子的な調和振動子の集まりとして取り扱う。固体の比熱の温度依存性を説明するために、アインシュタインが提案した固体の格子振動についての模型のこと。N個の同種原子からなる結晶の格子振動を、N個の独立な3次元調和振動子とみなし、しかも全てが同じ振動数を持つとした。
アインシュタイン模型では、格子振動の低周波領域が正しく扱われていないが、この点はデバイ模型によって改良された。
フォノン:
音子、音響量子、音量子は、振動(主に結晶中での格子振動)を量子化した粒子である。フォノンのひとつひとつがある振動数を持つモードの単位を表す。振幅が大きくなる、詰まり、振動が激しくなることはフォノンの数が増えることで表される。フォノンの持つエネルギーは格子の熱振動のエネルギーである。結晶格子のような周期構造中では、フォノンの振動数は制限され離散的になる。また、量子力学の効果で電子の場合と同様に、フォノンもバンド構造「フォノンバンド」を作る。
固体のフォノンは、音響フォノンと光学フォノンの2つに大別できる。音響フォノンは隣のフォトンと同じ位相で振動するが、光学フォノンは逆の位相で振動する。光(フォトン)と音響フォノンとの光散乱をブリルアン散乱という。光学フォノンは光と相互作用し、光と光学フォノンとの散乱をラマン散乱という。
グルナイセン・パラメータ:
結晶の格子振動の振動数は,結晶全体の体積Vによって変化する。この変化率は厳密には振動の各モードによって異なるが、近似的にこれを一定とし、振動数ν、またはデバイ温度Θの体積依存性をで表わし、γをグリュナイゼン定数という。γの値は物質により、また温度によるが1~2の程度である。体積熱膨張係数αは次の式であらわされる。
α=γCVκ/V
CV/Vは単位体積あたりの熱容量、κ=-(∂V/∂p)T/Vは等温圧縮率.格子振動が完全に調和的であればγ=0でなければならないから、熱膨張は格子振動の非調和性に由来するといってよい。
コーン(Kohn)異常:
金属における格子振動スペクトルに伝導電子のフェルミ球の効果によって出現する異常。
焦電性、焦電効果:
温度変化によって誘電体の分極(表面電荷)が変化する現象をいう。この現象を示す物質は、焦電体と呼ばれる。焦電体は圧電効果を示すので、圧電体の一種でもある。また、強誘電体は必ず焦電体である。電気石は焦電効果を示すことからこの名前が付けられた。
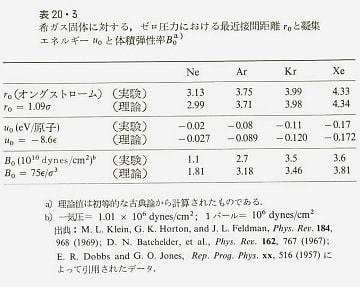
以下、本書に掲載されている図版を載せておこう。これらの図の原典は1960年代に書かれたれた教科書や論文から本書に引用されたものだ。








この教科書で学んでみようという方は、こちらからどうぞ。
「固体物理の基礎 上・1 固体電子論概論: アシュクロフト、マーミン」- 1981(紹介記事)
「固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン」- 1981(紹介記事)
「固体物理の基礎 下・1 固体フォノンの諸問題: アシュクロフト、マーミン」- 1981
「固体物理の基礎 下・2 固体の物性各論: アシュクロフト、マーミン」- 2008(紹介記事)




翻訳のもとになった英語版はこの本だ。1976年刊行。(2016年10月に追記: 改訂版「SOLID STATE PHYSICS REVISED EDITION: ASHCROFT MERMIN」が刊行された。)
「Solid State Physics 1e: Neil W. Ashcroft, N.David Mermin」(ハードカバー)(ペーパーバック)

関連ページ: ネットで学びたい方はこちらからどうぞ。
目で見て操作する「分子の世界」-そのミクロ構造と物性-
http://rikanet2.jst.go.jp/contents/cp0200a/start.html
物性物理学(筑波大学物理学系 小野田雅重先生のページ)
http://www.px.tsukuba.ac.jp/~onoda/cmp/cmp.html
ときわ台学:物質・材料の掟 (公開版)
http://www.f-denshi.com/000okite/000matrl.html
関連記事:
固体物理の基礎 上・1 固体電子論概論: アシュクロフト、マーミン
https://blog.goo.ne.jp/ktonegaw/e/af3b66dbda3564a4c49f5d7f722ad777
固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン
https://blog.goo.ne.jp/ktonegaw/e/8c12399f0dd9b78de128a9793502c3f3
固体物理の基礎 下・2 固体の物性各論: アシュクロフト、マーミン
https://blog.goo.ne.jp/ktonegaw/e/16c5344f47d2da648e2efabf8c020303
物性物理30講(物理学30講シリーズ):戸田盛和
https://blog.goo.ne.jp/ktonegaw/e/00d399f545bc69dfa213015f153a312a
基礎の固体物理学: 斯波弘行
https://blog.goo.ne.jp/ktonegaw/e/d2287a9fdbc66eac443fe0888d835602
分子軌道法: 物理学と化学の境界
https://blog.goo.ne.jp/ktonegaw/e/adb9c9e55a1ea2f1883b2a4bfced8f93
応援クリックをお願いします!







「固体物理の基礎 下・1 固体フォノンの諸問題: アシュクロフト、マーミン」

下・1:固体フォノンの諸問題
第19章:固体の分類
- 絶縁体の分類
- 価電子の空間分布
- 共有結合結晶と分子性結晶とイオン結晶
- アルカリ・ハライド結晶
- II-IV化合物とIII-V化合物
- 共有結合結晶
- 分子性結晶
- 金属
- 水素結合結晶
第20章:凝集エネルギー
- 希ガス:レナード-ジョーンズ・ポテンシャル
- 希ガス固体の密度と凝集エネルギーと体積弾性率
- イオン結晶:マーデルング定数
- アルカリ・ハライドの密度と凝集エネルギーと体積弾性率
- 共有結合結晶の凝集力
- 金属の凝集力
第21章:静止格子模型の破綻
- 平衡状態の性質
- 比熱
- 平衡密度と凝集エネルギー
- 熱膨張
- 融解
- 輸送的性質
- 電子緩和時間の温度依存性
- ヴィーデマン・フランツ法則の破綻
- 超伝導
- 絶縁体の熱伝導度
- 音の伝播
- 輻射との相互作用
- イオン結晶の屈折率
- 光の非弾性散乱
- X線の散乱
- 中性子の散乱
第22章:調和結晶の古典的理論
- 調和近似
- 断熱近似
- 古典的結晶の比熱:デュロン・プティの法則
- 1次元単原子ブラベー格子の基準振動
- 1次元の基本構造をもった格子の基準振動
- 3次元単原子ブラベー格子の基準振動
- 3次元の基本構造をもった格子の基準振動
- 弾性体論との関係
第23章:調和結晶の量子論
- 基準振動とフォノン
- 高温比熱
- 低温比熱
- デバイ模型とアインシュタイン模型
- 格子比熱と電子比熱の比較
- 基準振動の密度(フォノン準位密度)
- 黒体輻射の理論との類似
第24章:フォノン分散関係の測定
- 結晶による中性子散乱
- 結晶運動量
- 0-フォノン散乱
- 1-フォノン散乱
- 2-フォノン散乱
- 1-フォノン・ピークの幅
- 保存則と1-フォノン散乱
- 結晶による電磁波の散乱
- フォノン・スペクトルのX線測定
- フォノン・スペクトルの光学的測定
- 輻射と格子振動の相互作用の波動像
第25章:結晶の非調和効果
- 調和モデルが根本的に不適当な点
- 非調和理論の一般的な側面
- 結晶の状態方程式と熱膨張
- 熱膨張;グルナイセン・パラメータ
- 金属の熱膨張
- 格子熱伝導度:一般的扱い
- フォノン衝突
- 格子熱伝導度:初等的運動論
- 反転過程
- 第2音波
第26章:金属中のフォノン
- フォノンの分散関係の初等的な理論
- 音の速度
- コーン(Kohn)異常
- 金属の誘電定数
- 電子-電子間の有効相互作用
- 1電子エネルギーへのフォノンの寄与
- 電子-フォノン相互作用
- 金属の電気抵抗の温度依存性
- 反転過程の効果
- フォノン・ドラッグ
第27章:絶縁体の誘電的性質
- 巨視的静電的なマクスウェル方程式
- 局所場の理論
- クラウジウス・モソティの関係式
- 分極率の理論
- イオン結晶における長波長光学モード
- イオン結晶の光学的性質への応用
- 残留輻射
- 共有結合性絶縁体
- 焦電性および強誘電性結晶
付録
L:調和結晶の量子論
M:結晶運動量の保存
N:結晶による中性子の散乱の理論
O:非調和項とn-フォノン過程
その他の巻の章立て
上・1:固体電子論概論
第1章:金属のドゥルーデ(Drude)理論
第2章:金属のゾンマーフェルト理論
第3章:自由電子モデルの破綻
第4章:結晶格子
第5章:逆格子
第6章:X線回折による結晶構造の決定
第7章:ブラベー格子の分類と結晶構造の分類
第8章:周期ポテンシャル中の電子状態、一般的性質
第9章:弱い周期ポテンシャルの中の電子
第10章:強く束縛された方法
付録
上・2:固体のバンド理論
第11章:バンド構造を計算する他の方法
第12章:電子の動力学の半古典的モデル
第13章:金属伝導の半古典的理論
第14章:フェルミ面の測定
第15章:いくつかの金属のバンド構造
第16章:緩和時間近似を越えた近似
第17章:独立電子近似を越えた近似
第18章:表面効果
付録
下・2:半導体、磁性体、超伝導体論
第28章:均質な半導体
第29章:不均質な半導体
第30章:結晶中の欠陥
第31章:反磁性と常磁性
第32章:電子相互作用と磁気的構造
第33章:磁気的秩序
第34章:超伝導
付録
内容紹介:
学部生にも大学院生にも使えるよう工夫され、内容の取捨選択がしやすく、種々の目的、異なる水準でもうまく使い分けられる。固体物理学の現象の記述と理論的解析による統一という著者の目標は完全に達成されている。1981年刊行、282ページ。
著者について:
ニール・W・アシュクロフト(ウィキペディア、経歴詳細)
イギリスの物理学者(固体物理学)、1938年生。1958年ニュージーランド大学卒業。学位は1964年ケンブリッジ大学。シカゴ大学およびコーネル大学で博士研究員、1975年教授。1990年にHorace White Professor of Physics。2006年名誉教授。
デヴィッド・マーミン(ウィキペディア、ホームページ)
コーネル大学名誉教授(物理学)。米国物理学会のリリエンフェルト賞および米国物理教育学会のクロプステッグ賞を受賞。米国科学アカデミー、米国芸術科学アカデミーの会員。この数十年の間に、量子論の基礎的な問題に関する多くの著作を執筆しており、科学の啓蒙に関する明瞭さと機知には定評がある。
訳者について:
松原武生(まつばらたけお)
1921-2014 昭和後期-平成時代の理論物理学者。
大正10年4月3日生まれ。北大教授をへて昭和30年京大教授となる。61年岡山理大教授。誘電体、超伝導、超流動などを研究。「温度グリーン関数」の概念を提案した。36年仁科記念賞。日本物理学会会長をつとめた。平成26年12月15日死去。93歳。大阪府出身。大阪帝大卒。著作に「超流動と超伝導」「固体物理学」など。
町田一成(まちだかずしげ)
1968年東京教育大学理学部卒業。1973年同上理学研究科博士課程修了。京都大学理学部助手、岡山大学理学部助教授、教授を経て、岡山大学大学院自然科学研究科教授。
理数系書籍のレビュー記事は本書で280冊目。
3冊目に入ってからますますハードな勉強になってきた。固体の種類を分類した後、それぞれについて比熱や熱膨張率、熱伝導、電気抵抗、固体を伝わる音の速度など物性を計算する手順を解説する。
固体を伝わる熱は原子の格子振動による現象であること、その振動はフォノンや伝導電子によることは「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」という記事で大ざっぱに説明したことがあるが、本書ではそのことを固体物性の立場から詳細に解説、計算している。
結晶の静止格子模型がどのように破綻するか、そして静止模型から調和振動模型を採用して古典的、そして量子論的アプローチへと発展させる。それでもなお実験とのずれが生じるケースに対しては非調和振動模型を適用し、計算はますます複雑になっていく。
物理現象の中には調和振動理論では説明できないものが多数あり、それはイオン相互作用エネルギーをその平衡値の周りに展開したときの高次の項を無視したことによるものである。このような非調和項の存在が要求される現象には次のようなものがある。
- 調和結晶の量子論は比熱が高温でデュロン・プティの古典法則に従うことを予言するが、実際はそうならない。
- 非弾性的な中性子散乱の断面積は1-フォノン過程を支配する保存則によって許されたエネルギーのところで鋭いピークをもつが、実際に観測されるピークは相当明確なピークであっても観測可能な幅をもっている。1-フォノン・ピークの幅は、イオン相互作用エネルギーの非調和部分の強さのひとつの直接測定量である。
- 熱膨張は非調和項の存在で説明される。厳密に調和的な結晶では平衡状態の大きさは温度によらない。また弾性定数が体積にも温度にもよらないこと、断熱的と等温的とで弾性定数が等しくないことも非調和項によるものである。
- 絶縁固体の熱伝導度はイオン相互作用エネルギーの非調和項によってのみ有限におさえられる。厳密的に調和的な結晶は無限に大きい熱伝導度をもつと予測する。
固体の分類に従ったそれぞれのケースについて詳しく解説しているという意味ではとても優れた教科書だが、そのぶん記述がボリュームが増すことで「木を見て森を見ず。」の状況に陥りやすい。
僕はこの分野の専門家には絶対になれないと確信した1冊になった。後で思い出せるように、要点だけをこの記事にまとめておこう。
章立ては次のとおりだ。
下・1:固体フォノンの諸問題
第19章:固体の分類
第20章:凝集エネルギー
第21章:静止格子模型の破綻
第22章:調和結晶の古典論
第23章:調和結晶の量子論
第24章:フォノン分散関係の測定
第25章:結晶の非調和効果
第26章:金属中のフォノン
第27章:絶縁体の誘電的性質
付録
本書で特に重要なキーワードを解説しているページと短い説明を書いておこう。
分子性結晶(希ガス結晶):
典型的な例は希ガス固体つまりネオン、アルゴン、クリプトンとキセノンである。それらの原子状態は完全に占有された電子殻となっている。これは非常に安定した配置であり、固体になってもほんの少ししか変わらない。バンド構造という点から希ガスは強く束縛された固体の典型のよい例である。つまり電子密度はイオン芯の間ではほとんどなく、電子はすべてその属したイオンの近くに局在したままである。
注意:分子性結晶という表現は、分子間力以外の結合様式も入り込んだ場合用いる用語である。(分子結晶という表現との違いに注意。)
共有結合結晶:
共有結合によって形成される結晶のこと。一つの結晶粒で一つの分子(巨大分子)を形成しているため、化学式で表す際は形成される元素とその比率により表される。共有結合結晶とも呼ばれる。ダイヤモンドなどのように、共有結晶の中で各原子どうしは強い結合を形成する場合があり、その結果、融点が高かったり硬い性質を持つ場合がある。通常、電気伝導性はほとんどない。の他、ケイ素(シリコン)、二酸化ケイ素などが共有結晶を作る。
電子の空間分布としては、部分的にしか占有されていないバンドを持たない電子分布である。そのため結晶の電子はイオン芯の近くに鋭く局在している必要もない。また単純金属のように中間領域で、電子分布はほとんど一様ということでもない。
イオン結合結晶:
イオン結合によって形成される結晶のこと。この結晶は、異符号のイオン同士が隣り合いクーロン力によって結び付けられ固定されることでできる。イオン結合は強い結合なのでイオン結晶は融点が高く、硬い性質を持つ場合が多いが、脆くて壊れやすい性質も持つ。この性質を劈開という。これは、外力が加わると同符号のイオン同士が接近して、互いに反発しあうためである。通常、固体では電気伝導性はない(超イオン伝導体は例外)が、融点を超えて液体となった場合や溶質として水などに溶かすと電気を導く。これは、液体や水溶液になることで電荷を持ったイオンが移動できるようになるためである。水溶液中では電離して水和イオンとして存在する。このように水中で電離する物質を電解質という。
イオン結晶の最も素朴なモデルでは、すべてのイオンを貫通できない荷電球として扱う。結晶は正と負の荷電球の間の静電引力によって結合しており、球は貫通できないので結晶が壊れることはない。このように貫通できないのはパウリの排他原理やイオンの電子配置が安定な閉殻であることの結果である。二つのイオンを近づけるとその電子電荷分布は重なり始める。そのとき排他原理によって、各イオンの近くに他のイオンによって作られた過剰な電荷は占有されていない状態に収容されることになる。しかし正と負のイオンの電子配置は安定な閉殻である。これは占有状態と最低非占有状態の間に大きなエネルギー・ギャップが存在することを意味する。その結果、電荷分布を無理に重なり合わせるのには非常に多くのエネルギーを必要とする。つまりイオンを近づけて電子電荷分布が互いに重なり合うと強い反発力がそのイオン間に働く。
水素結合結晶(分子結晶):
結晶のうち、分子同士の親和力として主に水素結合を利用して形成されているもののこと。水素結合性結晶とも呼ばれる。もっとも身近で代表的な水素結合結晶は氷である。通常の水素結合はファン・デル・ワールス力よりも強いため、同程度の分子量の化合物で比べた場合、水素結合結晶のほうがファンデルワールス結晶よりも格子エネルギーが大きい、すなわち融点が高いことが多い。
ファンデルワールス結晶(分子結晶):
分子間力の一種であるファンデルワールス力によって形成される結晶のこと。ファンデルワールス力による結合は弱いので、分子結晶の格子エネルギーは弱く、融点が低かったり、柔らかかったり、昇華性を持ったりする場合が多い。主な例として、ドライアイスやナフタレン、非極性の高分子化合物などがあげられる。
一般に、静電相互作用や水素結合などのより強い分子間相互作用がはたらかないような分子が結晶となる場合にとる形式である。
金属:
金属を原子の化学結合で定義する場合、特有の金属結合で説明される。これは、カチオン化した金属元素が規則正しく並び、その間を自由電子が動き回りながら、これらがクーロン力で結びついている結合を指し、常温下でこのような結合状態にある物質を金属と定義している。原子の配列は、ほとんどの場合、面心立方格子構造 (fcc)、体心立方格子構造 (bcc)、六方最密充填構造 (hcp) のいずれかを取り、元素の種類や同じ元素でも状態によってそれぞれの構造となる。この構造はそれぞれ原子充填率が異なり、金属の塑性変形に影響を与える。
金属の定義や分類はウィキペディアの項目を参照していただきたい。
周期表をIV族から左にいくと金属の族に行きつく。共有結合が拡がり、すき間の領域全体にも電子密度が認められ、k-空間(波数ベクトル空間)ではバンドが重なり合う。金属結晶の重要な例はI族のアルカリ金属である。それらの金属は多くの目的に対してはゾンマーフェルトの自由電子模型よって正確に記述できる。この模型では価電子はイオン芯から完全に分離しており、ほとんど一様な気体を形成する。さらに一般的なことであるが、金属においてさえ共有結合や分子性結合の性質がみられる。とくに貴金属では占有されている原子のd殻はあまりきつく束縛されておらず、その結果金属中ではかなり歪んでいる。
凝集エネルギー:
液体や固体など、凝集状態にある原子またはイオンを、互いに引き離してばらばらにするために必要なエネルギー。
マールディング定数:
イオン結晶において、静電気的なポテンシャルエネルギーを表す定数をマーデルング定数と呼び、結晶構造の種類により決まる定数である。(ウィキペディアの「マールディングエネルギー」を参照。)
ヴィーデマン・フランツ法則:
金属の熱伝導率Kと、電気伝導率σの比が温度に比例することを示したものである。金属の場合、熱伝導と電気伝導の両方の大部分を自由電子が担うので、この関係が成り立っている。
デュロン・プティの法則:
固体元素の定積モル比熱 C_V が常温付近(デバイ温度より大きい領域)ではどれもほとんど等しく、 C_V = 3R = 3N_Ak_B ( = 5.96 cal/mol・K、 R は気体定数、 N_A , k_B はそれぞれアヴォガドロ定数とボルツマン定数)であるという法則。エネルギー等配分の法則やデバイ模型から導出できる。
デバイ模型:
熱力学と固体物理学において、固体におけるフォノンの比熱(熱容量)への寄与を推定する手法である。デバイ模型では、原子の熱による格子振動を箱の中のフォノンとして扱う。デバイ模型は低温における比熱のT^3に比例する温度依存性を正しく予言する。また比熱の高温におけるデュロン=プティの法則に従う振る舞いも正しく説明することができる。しかし格子振動を単純化して扱っているため、中間的な温度における正確性には弱点がある。
アインシュタイン模型:
熱力学と固体物理学において、固体を相互作用のない量子的な調和振動子の集まりとして取り扱う。固体の比熱の温度依存性を説明するために、アインシュタインが提案した固体の格子振動についての模型のこと。N個の同種原子からなる結晶の格子振動を、N個の独立な3次元調和振動子とみなし、しかも全てが同じ振動数を持つとした。
アインシュタイン模型では、格子振動の低周波領域が正しく扱われていないが、この点はデバイ模型によって改良された。
フォノン:
音子、音響量子、音量子は、振動(主に結晶中での格子振動)を量子化した粒子である。フォノンのひとつひとつがある振動数を持つモードの単位を表す。振幅が大きくなる、詰まり、振動が激しくなることはフォノンの数が増えることで表される。フォノンの持つエネルギーは格子の熱振動のエネルギーである。結晶格子のような周期構造中では、フォノンの振動数は制限され離散的になる。また、量子力学の効果で電子の場合と同様に、フォノンもバンド構造「フォノンバンド」を作る。
固体のフォノンは、音響フォノンと光学フォノンの2つに大別できる。音響フォノンは隣のフォトンと同じ位相で振動するが、光学フォノンは逆の位相で振動する。光(フォトン)と音響フォノンとの光散乱をブリルアン散乱という。光学フォノンは光と相互作用し、光と光学フォノンとの散乱をラマン散乱という。
グルナイセン・パラメータ:
結晶の格子振動の振動数は,結晶全体の体積Vによって変化する。この変化率は厳密には振動の各モードによって異なるが、近似的にこれを一定とし、振動数ν、またはデバイ温度Θの体積依存性をで表わし、γをグリュナイゼン定数という。γの値は物質により、また温度によるが1~2の程度である。体積熱膨張係数αは次の式であらわされる。
α=γCVκ/V
CV/Vは単位体積あたりの熱容量、κ=-(∂V/∂p)T/Vは等温圧縮率.格子振動が完全に調和的であればγ=0でなければならないから、熱膨張は格子振動の非調和性に由来するといってよい。
コーン(Kohn)異常:
金属における格子振動スペクトルに伝導電子のフェルミ球の効果によって出現する異常。
焦電性、焦電効果:
温度変化によって誘電体の分極(表面電荷)が変化する現象をいう。この現象を示す物質は、焦電体と呼ばれる。焦電体は圧電効果を示すので、圧電体の一種でもある。また、強誘電体は必ず焦電体である。電気石は焦電効果を示すことからこの名前が付けられた。
以下、本書に掲載されている図版を載せておこう。これらの図の原典は1960年代に書かれたれた教科書や論文から本書に引用されたものだ。









この教科書で学んでみようという方は、こちらからどうぞ。
「固体物理の基礎 上・1 固体電子論概論: アシュクロフト、マーミン」- 1981(紹介記事)
「固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン」- 1981(紹介記事)
「固体物理の基礎 下・1 固体フォノンの諸問題: アシュクロフト、マーミン」- 1981
「固体物理の基礎 下・2 固体の物性各論: アシュクロフト、マーミン」- 2008(紹介記事)




翻訳のもとになった英語版はこの本だ。1976年刊行。(2016年10月に追記: 改訂版「SOLID STATE PHYSICS REVISED EDITION: ASHCROFT MERMIN」が刊行された。)
「Solid State Physics 1e: Neil W. Ashcroft, N.David Mermin」(ハードカバー)(ペーパーバック)

関連ページ: ネットで学びたい方はこちらからどうぞ。
目で見て操作する「分子の世界」-そのミクロ構造と物性-
http://rikanet2.jst.go.jp/contents/cp0200a/start.html
物性物理学(筑波大学物理学系 小野田雅重先生のページ)
http://www.px.tsukuba.ac.jp/~onoda/cmp/cmp.html
ときわ台学:物質・材料の掟 (公開版)
http://www.f-denshi.com/000okite/000matrl.html
関連記事:
固体物理の基礎 上・1 固体電子論概論: アシュクロフト、マーミン
https://blog.goo.ne.jp/ktonegaw/e/af3b66dbda3564a4c49f5d7f722ad777
固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン
https://blog.goo.ne.jp/ktonegaw/e/8c12399f0dd9b78de128a9793502c3f3
固体物理の基礎 下・2 固体の物性各論: アシュクロフト、マーミン
https://blog.goo.ne.jp/ktonegaw/e/16c5344f47d2da648e2efabf8c020303
物性物理30講(物理学30講シリーズ):戸田盛和
https://blog.goo.ne.jp/ktonegaw/e/00d399f545bc69dfa213015f153a312a
基礎の固体物理学: 斯波弘行
https://blog.goo.ne.jp/ktonegaw/e/d2287a9fdbc66eac443fe0888d835602
分子軌道法: 物理学と化学の境界
https://blog.goo.ne.jp/ktonegaw/e/adb9c9e55a1ea2f1883b2a4bfced8f93
応援クリックをお願いします!




「固体物理の基礎 下・1 固体フォノンの諸問題: アシュクロフト、マーミン」

下・1:固体フォノンの諸問題
第19章:固体の分類
- 絶縁体の分類
- 価電子の空間分布
- 共有結合結晶と分子性結晶とイオン結晶
- アルカリ・ハライド結晶
- II-IV化合物とIII-V化合物
- 共有結合結晶
- 分子性結晶
- 金属
- 水素結合結晶
第20章:凝集エネルギー
- 希ガス:レナード-ジョーンズ・ポテンシャル
- 希ガス固体の密度と凝集エネルギーと体積弾性率
- イオン結晶:マーデルング定数
- アルカリ・ハライドの密度と凝集エネルギーと体積弾性率
- 共有結合結晶の凝集力
- 金属の凝集力
第21章:静止格子模型の破綻
- 平衡状態の性質
- 比熱
- 平衡密度と凝集エネルギー
- 熱膨張
- 融解
- 輸送的性質
- 電子緩和時間の温度依存性
- ヴィーデマン・フランツ法則の破綻
- 超伝導
- 絶縁体の熱伝導度
- 音の伝播
- 輻射との相互作用
- イオン結晶の屈折率
- 光の非弾性散乱
- X線の散乱
- 中性子の散乱
第22章:調和結晶の古典的理論
- 調和近似
- 断熱近似
- 古典的結晶の比熱:デュロン・プティの法則
- 1次元単原子ブラベー格子の基準振動
- 1次元の基本構造をもった格子の基準振動
- 3次元単原子ブラベー格子の基準振動
- 3次元の基本構造をもった格子の基準振動
- 弾性体論との関係
第23章:調和結晶の量子論
- 基準振動とフォノン
- 高温比熱
- 低温比熱
- デバイ模型とアインシュタイン模型
- 格子比熱と電子比熱の比較
- 基準振動の密度(フォノン準位密度)
- 黒体輻射の理論との類似
第24章:フォノン分散関係の測定
- 結晶による中性子散乱
- 結晶運動量
- 0-フォノン散乱
- 1-フォノン散乱
- 2-フォノン散乱
- 1-フォノン・ピークの幅
- 保存則と1-フォノン散乱
- 結晶による電磁波の散乱
- フォノン・スペクトルのX線測定
- フォノン・スペクトルの光学的測定
- 輻射と格子振動の相互作用の波動像
第25章:結晶の非調和効果
- 調和モデルが根本的に不適当な点
- 非調和理論の一般的な側面
- 結晶の状態方程式と熱膨張
- 熱膨張;グルナイセン・パラメータ
- 金属の熱膨張
- 格子熱伝導度:一般的扱い
- フォノン衝突
- 格子熱伝導度:初等的運動論
- 反転過程
- 第2音波
第26章:金属中のフォノン
- フォノンの分散関係の初等的な理論
- 音の速度
- コーン(Kohn)異常
- 金属の誘電定数
- 電子-電子間の有効相互作用
- 1電子エネルギーへのフォノンの寄与
- 電子-フォノン相互作用
- 金属の電気抵抗の温度依存性
- 反転過程の効果
- フォノン・ドラッグ
第27章:絶縁体の誘電的性質
- 巨視的静電的なマクスウェル方程式
- 局所場の理論
- クラウジウス・モソティの関係式
- 分極率の理論
- イオン結晶における長波長光学モード
- イオン結晶の光学的性質への応用
- 残留輻射
- 共有結合性絶縁体
- 焦電性および強誘電性結晶
付録
L:調和結晶の量子論
M:結晶運動量の保存
N:結晶による中性子の散乱の理論
O:非調和項とn-フォノン過程
その他の巻の章立て
上・1:固体電子論概論
第1章:金属のドゥルーデ(Drude)理論
第2章:金属のゾンマーフェルト理論
第3章:自由電子モデルの破綻
第4章:結晶格子
第5章:逆格子
第6章:X線回折による結晶構造の決定
第7章:ブラベー格子の分類と結晶構造の分類
第8章:周期ポテンシャル中の電子状態、一般的性質
第9章:弱い周期ポテンシャルの中の電子
第10章:強く束縛された方法
付録
上・2:固体のバンド理論
第11章:バンド構造を計算する他の方法
第12章:電子の動力学の半古典的モデル
第13章:金属伝導の半古典的理論
第14章:フェルミ面の測定
第15章:いくつかの金属のバンド構造
第16章:緩和時間近似を越えた近似
第17章:独立電子近似を越えた近似
第18章:表面効果
付録
下・2:半導体、磁性体、超伝導体論
第28章:均質な半導体
第29章:不均質な半導体
第30章:結晶中の欠陥
第31章:反磁性と常磁性
第32章:電子相互作用と磁気的構造
第33章:磁気的秩序
第34章:超伝導
付録





















目標に向かって頑張って勉強してください。
けれどもいただいたコメントはこのページ「固体物理の基礎 下・1 」と関係ありません。
もし引き続きワインバーグの宇宙論の教科書についてコメントされる場合は、次の記事のコメント欄に投稿していただきますようお願いします。
発売情報:ワインバーグの宇宙論(上)(下)
http://blog.goo.ne.jp/ktonegaw/e/3aab4560e20f675285c35002fc96dfab
もし、今後この記事にコメントいただいた場合は公開を非承認(無視)させていただきますのでご注意ください。
ワインバーグの宇宙論の上巻の最初のほうを理解するためには一般相対性理論を理解しておく必要があります。「どう役に立てればいいですか?」ということですが日本評論社の「一般相対論入門」と「もうひとつの一般相対論入門」はワインバーグの宇宙論を読むために直接役に立ちます。
ちなみに一般相対性理論の教科書のほうがワインバーグの宇宙論の教科書より易しいですよ。
ところでいまさらですがコメントはこのページ「固体物理の基礎 下・1 」と関係ありません。
もし引き続きワインバーグの宇宙論の教科書についてコメントされる場合は、次の記事のコメント欄に投稿していただきますようお願いします。
発売情報:ワインバーグの宇宙論(上)(下)
http://blog.goo.ne.jp/ktonegaw/e/3aab4560e20f675285c35002fc96dfab
大著ですのでポイントを絞るということはほとんど無理ですが、あえて言うならば次のようなことに注意してお読みになるとよいでしょう。
1)宇宙膨張の箇所では期間を区切って説明していますから、どの期間のことかを常に意識して忘れないこと。
2)宇宙を構成する素粒子や物質のそれぞれについて式を立てて説明しているので、長い説明を読んでいるうちにどの素粒子、物質のことかを忘れがちになります。忘れないように注意を払うこと。
3)宇宙の揺らぎについては摂動論を使いますが、スカラー型摂動とテンソル型摂動をきちんと区別して理解すること。
この教科書は時間や論じている対象の違いにより、説明が数多く「場合分け」されているので、混乱しないようにメモを取りながらお読みになるとよいでしょう。
そのように高度なことを目指しているのですね。
残念ながら僕は超準解析を学んだことがないので「解析入門を超準解析に書き換えられるのかどうか」についてはわかりません。
ε-δ論法の理解にこだわっていたのは、そのようなわけでしたか。納得しました。
ワインバーグの宇宙論はいちばん難しい本のうちのひとつです。「宇宙の楽しさに触れられる。」などとは書いたことはありませんよ。おそらく「完全独習現代の宇宙論」も難しすぎると思います。(サトシさんは解析学を学んでいる途中の段階だということは存じていますので。)
ワインバーグの宇宙論の本の難しさは、この記事に書きました。
ワインバーグの宇宙論(上)ビッグバン宇宙の進化
http://blog.goo.ne.jp/ktonegaw/e/bd3d49fe1e13bcdd97116b33e8c736bb
ワインバーグの宇宙論(下): ゆらぎの形成と進化
http://blog.goo.ne.jp/ktonegaw/e/13c2b81456935c281b4c57a014cd9d60
宇宙論の易しい本でしたら次のものをお勧めします。
下にいけばいくほど易しくなります。
宇宙創成はじめの3分間 (ちくま学芸文庫):ワインバーグ
宇宙に果てはあるか (新潮選書) :吉田伸夫
宇宙創成〈上〉〈下〉 (新潮文庫) :サイモン・シン
ホーキング、宇宙を語る―ビッグバンからブラックホールまで (ハヤカワ文庫NF)
宇宙が始まる前には何があったのか?:ローレンス・クラウス
みるみる理解できる宇宙論 第2版―(ニュートンムック Newton別冊サイエンステキストシリーズ)
この3つです。
初歩からの数学('12)の第13回ーテレビ
http://www.ouj.ac.jp/hp/kamoku/H27/kyouyou/B/kiso/1234030.html
微分と積分('10)の第3回ーテレビ
http://www.ouj.ac.jp/hp/kamoku/H27/kyouyou/B/ippan_shizen/1131702.html
解析入門('14)の第1回ーラジオ
http://www.ouj.ac.jp/hp/kamoku/H27/kyouyou/B/ippan_shizen/1234200.html
番組表を見ると、ちょうど今日の夕方5時半から実数の連続性の内容を含む回が放送されます。なんというグッドタイミングでしょう!お見逃しなく!
http://www.ouj.ac.jp/hp/bangumi2/bangumi.php
10月21日午後5時半から
微分と積分(’10)
第3回 上限・下限、関数の極限値
極限値の基本性質を解説し、連続関数を定義する。議論の基礎として実数の連続性について述べ、数集合の上限と下限、関数の最大値と最小値について解説する。
担当講師:熊原 啓作(放送大学名誉教授) 押川 元重(放送大学客員教授)
宇宙論関係の易しい本は先月以下の本を紹介させていただきましたよ。お忘れですか?まず、それらをお読み下さい。
下にいけばいくほど易しくなります。
宇宙創成はじめの3分間 (ちくま学芸文庫):ワインバーグ
宇宙に果てはあるか (新潮選書) :吉田伸夫
宇宙創成〈上〉〈下〉 (新潮文庫) :サイモン・シン
ホーキング、宇宙を語る―ビッグバンからブラックホールまで (ハヤカワ文庫NF)
宇宙が始まる前には何があったのか?:ローレンス・クラウス
みるみる理解できる宇宙論 第2版―(ニュートンムック Newton別冊サイエンステキストシリーズ)
宇宙論関係の本がいいです。
タイプミスのご指摘、とてもありがたかったです。本文記事を修正しておきました。
もっと読み直してから投稿すればよかったです。
ありがとうございました。
等しくなことも→等しくないことも
イオンを近づけるとその電子電荷分布は互いに重なり合うといつも強い反発力→
イオンを近づけて電子電荷分布が互いに重なり合うと強い反発力