次の数式をプログラミングしろ。
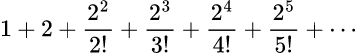
Python:
from functools import reduce
from math import factorial
from fractions import Fraction
def foo(n):
return reduce(lambda ini, x: ini + Fraction(2 ** x, factorial(x)),\
range(n+1), 0)
# 別解
def bar(n):
return sum([Fraction(2 ** x, factorial(x)) for x in range(n+1)])
Racket:
(require math/number-theory)
(define (foo n)
(foldl (lambda (y x)
(+ x (/ (expt 2 y) (factorial y))))
0 (range (add1 n))))
;; 別解
(define (bar n)
(apply + (map (lambda (x)
(/ (expt 2 x) (factorial x))) (range (add1 n)))))
JavaScript:
let range = n => [...Array(n).keys()]
function factorial(n) {
return range(n + 1).slice(1).reduce(
(x, y) => x * y,
1
);
}
function foo(n) {
return range(n+1).reduce(
(x, y) => x + Math.pow(2, y) / factorial(y),
0
);
}
// 別解function bar(n) {
return range(n + 1).map((x) => Math.pow(2, x) / factorial(x)).reduce((x, y) => x + y, 0);
}
Ruby:
def factorial(n)
(1..n).to_a.inject (1){|x, y| x * y}
end
def foo(n)
(0..n).to_a.inject (0) {|x, y| x + Rational(2 ** y, factorial(y))}
end
# 別解
def bar(n)
(0..n).to_a.map {|x| Rational(2 ** x, factorial(x))}.sum
end
ここではPython、Racket、JavaScript、Rubyの4つで解題を試みている。
前者2つは階乗計算のライブラリ関数(factorial)があるケース、後者2つは階乗計算のライブラリ関数が無いんで、自作せねばならないケースだ。
階乗計算は再帰の練習代わりに良く使われるお題なんだけど、個人的には飽きたんで(笑)、使えるモノがあれば使う、と言う割り切った状態になっている。
もちろん、高階関数foldやreduceの使い方のお題、としては悪くはない。関数factorialを定義する為にJavaScriptではreduceメソッドを用い、Rubyでは同様の機能を持ってるinjectメソッドを用いてる。
PythonやLispでもあくまでreduceやfoldの練習課題としてfactorialを自作しても良いだろう。
ただし、Lispでは、正直言うと、factorialを自作したりするのに再帰やreduce/foldを使う必要はないんだ。ついつい、他の言語のお題でのティピカルな課題なんで、Lispでも「そうしなきゃいけない」気になってくるけど、実はLisp系言語の場合、Pythonのrangeにあたる関数さえあればfactorialはこんな風にすぐ書けてしまう。
(define (factorial n)
(apply * (cons 1 (cdr (range (add1 n))))))
これがLisp系言語に於ける、一番シンプルな階乗計算の関数定義だ。
何故これが一番シンプルだ、と言えるんだろう。それはLispの四則演算子の強力さをそのまま利用してるから、だ。
Lisp系言語と他のプログラミング言語の大きな違いは、Lisp系言語では四則演算さえおかしな(笑)前置記法になってる、って辺りだが、それがLisp系言語での四則演算の強力さを支えてる。
他の言語では四則演算が中置記法な為、2つの被演算子しか取れない、と言う限界があるが、Lisp系言語の場合可変長引数を取る。すなわち、被演算子がいくつあろうと全く構わないわけだ。
Pythonのsum関数は非常に便利だが、何故にLispにsumが無いのか、と言うのもこれが理由だ。数のリストとapplyと+があれば同様の結果をハナクソをほじり出す前に得る事が出来る。
さて、ここで挙げた言語ではそれぞれ、reduce/fold中心で解く解と、mapとsum中心で解く解の2つを挙げてある。前者は問題に従ってまさしく「畳み込んで」行くが、後者はリストとして要素をそれぞれ計算して、その総和を取る形式だ。
なるたけ、どっちも書けるようにしておこう。何度も言うが、mapとreduceはその歴史的な重みと共に重要度が極めて高い、高階関数の最高傑作だ。
なお、isamさんがVisual Basicでの解法を試みてる。さすがにVisualBasicは高階関数なんぞが無い非力な言語だが、isamさんの書いてるのは「フツーのプログラミング言語でのフツーの書き方(例えばCとかPascalとか)ではこうなる」と言う参考になると思う。
以上。