テニス（ダブルス）組合せ表

今月のパソコン教室で久し振りに Excel を使い「能力テスト」の作表を習った。家に帰って復習してみてこれを乱数で作ってみたくなり調べたら乱数を表わす関数が見つかった、試してみたら結構面白い表ができた。

考えてみるといつもテニス仲間で集まり市営の施設を借りてプレーをするがその時の組合せ表も乱数表を利用しているのだと思い当たった。そこで作る事に挑戦してみた。

まず集まる人に番号を付ける。その人数を4人から9人までの範囲で試合数を30ゲーム位としてやってみる事にした。
最初に各人数毎に幾つのペアが出来るかを数えてみる事にすると
　　4人　　6組　　5人　10組　　6人　15組
　　7人　21組　　8人　28組　　9人　36組　　　と云うようになった、
これを元に対戦カードの組合せ（試合数）を計算すると下記の様になる、尚、7人から9人の表は組合せの数が多すぎるので省略します。
　　4人　３ゲーム　　　    5人１０ゲーム　　　  6人　４５ゲーム
　　7人　１０５ゲーム　　　8人　２１０ゲーム　  9人　３７８ゲーム

ここで対戦カードごとに１から番号を振りその範囲内で乱数を発生させて30ゲーム分の組合せを決めました。但し、4人参加のグループは3組のゲームの繰り返しなので省きました。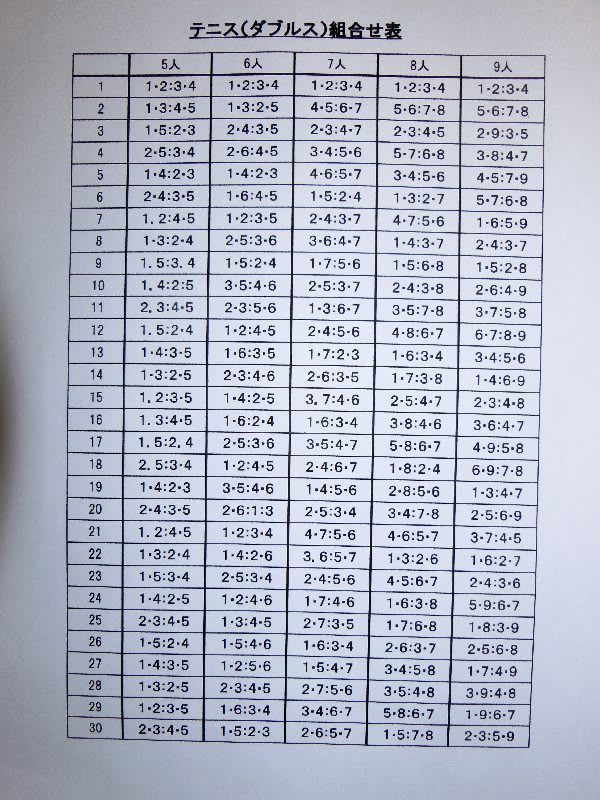

この表では出来る限り同じ人が５回以上連続したり、同じペアがやはり続けて試合をするのは好ましく無いのでそこは手作業で調整しました。（器械だけの計算ではどうしても起きる事なので）

そして対戦カードの表を作る過程で面白い事が解ってきた。
まず、ペアの組合せ（対戦相手）の数をペアの数で割るとＡが求められる、その数を人数毎の差を求め更にその差を計算すると全てが ０．５ になった。これは何となく式が潜んでいるなと思い以前買っておいた高校数学の教科書をひっぱりだして調べ出すと数学Ｂの数列、斬化式の処に行きついた。
それを参考に係数 A の式  A=0.5+0.25(n-1)(n-4) を導き出し、対戦カードの数を計算する式を見つけ出す事が出来た。T=(n-2)C2*A  （この式のＣの前後にある（n－２）と２は添え字として普通は小さい文字で組合せの計算式です）。私としてはどうしてこの様な式が出来たか解りませんが、多分専門家の先生方なら論理的に説明出来るでしょう。残念ながら私にはそこまでの能力も体力も持ち合わせていません。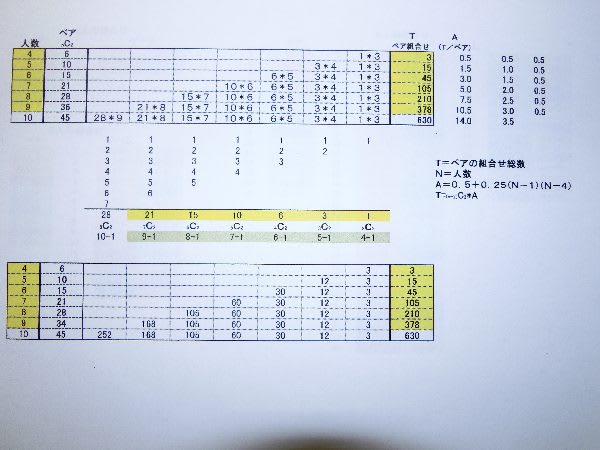

この1週間、この表を作る事にはまりサイクリングやテニスの後も、絶えず頭の隅にあり疲れていてもどうしたら作れるのか考え通しで０時過ぎまで起きている事も数回あり、やっと今日出来上がりました。とてもバテてます。