どもども。
前回に引き続き，今年の東北大入試(後期)理系数学の第1問をやっていきます～
問題はこちら
前回：http://blog.goo.ne.jp/mathnegi/e/fab5be206484546f5b690be5269a4275
今回も(1)についてやっていきます～
前回は主に２^x=X，３^y＝Ｙなどと変数変換して解く標準的な解法パターンで
取り組んでみましたが，今回は変数変換しないで2変数の指数関数だと思って
問題の条件式が表す領域を考えて解くパターンを考察してみます
無論，標準的な解法よりもめんどくさいです
敢えてやってみる，という趣旨でやっていきましょう～
問題文で与えられているのは
4^x-4・2^x+9^y-2・3^y≦－１ という不等式です。
そこで，ℓ≦－1を満たすℓに対して曲線 4^x-4・2^x+9^y-2・3^y＝ℓ を考えます
ℓを変化させて，この曲線の軌跡を調べることによって
4^x-4・2^x+9^y-2・3^y≦－１ が表す領域Ｄを把握することが出来ます
4^x-4・2^x+9^y-2・3^y＝ℓ を「ｙ＝」のかたちで表示します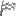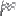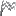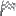
まずはｆ（ｘ）について考えていきましょう～
f(x)=log(
)の形をしていますが＞０なので真数条件は常にクリアしてますね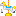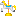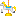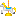
でもｘの動きうる範囲は全実数では無さそうです。
また，ℓの値によっても曲線の形が違ってきそうです。
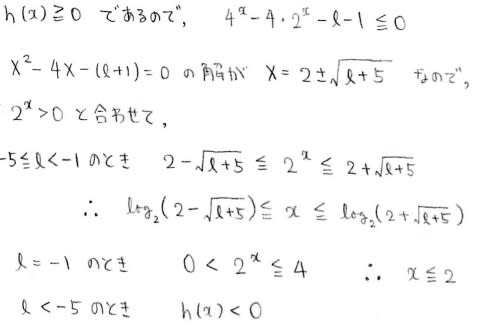
ℓ＜－５のときは曲線上の(x，y)は存在しないようですから
－５≦ℓ≦－１の場合を考えればよい，そしてℓ＝－１の場合だけ形が他と違う，
とりあえずそういうことが分かりました
それでは微分して増減を調べてグラフを描いてみましょう～
ℓ＝－１のときだけｘ→－∞のときf(x)→０となっていて
－５≦ℓ＜－１のときはℓ＝－１の曲線をクシュッと萎ませたような形になっているようです
次はｙ＝ｇ（ｘ）について考えましょう。今度は真数条件も必要です。
今回も－５≦ℓ≦－１の場合を考えればよさそうですね
なんとか問題文の条件式が表す領域を図示することが出来ました
領域Dの境界は上下ともℓ＝－１のときの曲線になっています～
この領域と曲線 2^x+3^y=k が共有点を持つようなｋの範囲を求めればいいわけですね！！
ｙ＝F(x)のグラフは右下がりの曲線であることが分かりました。
どうも第１象限で領域Ｄと接することがありそうですよね。
第４象限では微妙です
まずは第１象限で接するときのｋを求めてしまいます。
なんともウンザリする連立方程式
解く気なんか起きやしません。て言うかキレイに解けるのかコレ
…と思って式をいじってみたら，意外とイケたりしました
ｙ＝Ｆ（ｘ）のグラフはｘ＝log_2 (k)を漸近線として持つので，とりあえず
log_2 (２－√３)＜ｋ≦３＋２√２ のときは，ｙ＝Ｆ（ｘ）のグラフは領域Ｄと共有点を必ず持ちます
では，log_2 (２－√３)≧ｋ のときはどうなんでしょう。
実は常にｙ＝Ｆ（ｘ）のグラフは領域Ｄの下側に位置して，そのおかげで共有点を持たなくなってしまいます。
そのことをこれから確かめていきます
ちなみに境界曲線とｙ＝Ｆ（ｘ）のグラフが交点を持たないことを示せばＯＫです～
漸近線 ｙ＝log_3 (k)（＜０） がｙ＝０より下側にあるため，境界曲線との交点が無ければ常にｙ＝Ｆ（ｘ）のグラフのほうが境界曲線より下にあります。
交点を持つと仮定して矛盾を導く，すなわち背理法！
それを試してみましょう
いま求めたｔが０＜ｔ＜ｋを満たさないことを確かめるには，
ｋ≦ｔとなっていることを言えばよいわけです
以上をまとめて，答えの範囲を得る，ということでおしまいです
おとなしく変数変換してとくほうが何倍も早いし明瞭ですね
お疲れ様でした
前回に引き続き，今年の東北大入試(後期)理系数学の第1問をやっていきます～
問題はこちら
前回：http://blog.goo.ne.jp/mathnegi/e/fab5be206484546f5b690be5269a4275
今回も(1)についてやっていきます～
前回は主に２^x=X，３^y＝Ｙなどと変数変換して解く標準的な解法パターンで
取り組んでみましたが，今回は変数変換しないで2変数の指数関数だと思って
問題の条件式が表す領域を考えて解くパターンを考察してみます
無論，標準的な解法よりもめんどくさいです
敢えてやってみる，という趣旨でやっていきましょう～
問題文で与えられているのは
4^x-4・2^x+9^y-2・3^y≦－１ という不等式です。
そこで，ℓ≦－1を満たすℓに対して曲線 4^x-4・2^x+9^y-2・3^y＝ℓ を考えます
ℓを変化させて，この曲線の軌跡を調べることによって
4^x-4・2^x+9^y-2・3^y≦－１ が表す領域Ｄを把握することが出来ます
4^x-4・2^x+9^y-2・3^y＝ℓ を「ｙ＝」のかたちで表示します
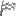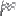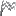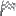
まずはｆ（ｘ）について考えていきましょう～
f(x)=log(
)の形をしていますが＞０なので真数条件は常にクリアしてますね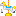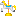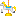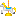でもｘの動きうる範囲は全実数では無さそうです。
また，ℓの値によっても曲線の形が違ってきそうです。
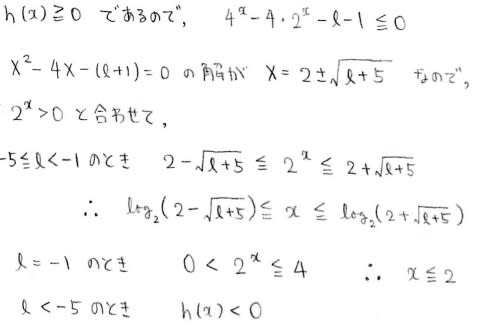
ℓ＜－５のときは曲線上の(x，y)は存在しないようですから
－５≦ℓ≦－１の場合を考えればよい，そしてℓ＝－１の場合だけ形が他と違う，
とりあえずそういうことが分かりました
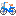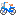
それでは微分して増減を調べてグラフを描いてみましょう～
ℓ＝－１のときだけｘ→－∞のときf(x)→０となっていて
－５≦ℓ＜－１のときはℓ＝－１の曲線をクシュッと萎ませたような形になっているようです
次はｙ＝ｇ（ｘ）について考えましょう。今度は真数条件も必要です。
今回も－５≦ℓ≦－１の場合を考えればよさそうですね
なんとか問題文の条件式が表す領域を図示することが出来ました
領域Dの境界は上下ともℓ＝－１のときの曲線になっています～
この領域と曲線 2^x+3^y=k が共有点を持つようなｋの範囲を求めればいいわけですね！！
ｙ＝F(x)のグラフは右下がりの曲線であることが分かりました。
どうも第１象限で領域Ｄと接することがありそうですよね。
第４象限では微妙です
まずは第１象限で接するときのｋを求めてしまいます。
なんともウンザリする連立方程式
解く気なんか起きやしません。て言うかキレイに解けるのかコレ
…と思って式をいじってみたら，意外とイケたりしました
ｙ＝Ｆ（ｘ）のグラフはｘ＝log_2 (k)を漸近線として持つので，とりあえず
log_2 (２－√３)＜ｋ≦３＋２√２ のときは，ｙ＝Ｆ（ｘ）のグラフは領域Ｄと共有点を必ず持ちます
では，log_2 (２－√３)≧ｋ のときはどうなんでしょう。
実は常にｙ＝Ｆ（ｘ）のグラフは領域Ｄの下側に位置して，そのおかげで共有点を持たなくなってしまいます。
そのことをこれから確かめていきます
ちなみに境界曲線とｙ＝Ｆ（ｘ）のグラフが交点を持たないことを示せばＯＫです～
漸近線 ｙ＝log_3 (k)（＜０） がｙ＝０より下側にあるため，境界曲線との交点が無ければ常にｙ＝Ｆ（ｘ）のグラフのほうが境界曲線より下にあります。
交点を持つと仮定して矛盾を導く，すなわち背理法！
それを試してみましょう
いま求めたｔが０＜ｔ＜ｋを満たさないことを確かめるには，
ｋ≦ｔとなっていることを言えばよいわけです
以上をまとめて，答えの範囲を得る，ということでおしまいです
おとなしく変数変換してとくほうが何倍も早いし明瞭ですね
お疲れ様でした