どもども。
前回に引き続いて今年の春の長野県の公立入試問題を取り上げますね
今回取り扱うのは最後の大問である第4問です。
円や相似が絡んだ入試問題鉄板の図形問題です。
問題と解答はこちらから見られます。
http://www.pref.nagano.lg.jp/kyouiku/kyougaku/koukounuusi/index24.htm
前回も述べたように,全体的に難易度が高く問題数も非常に多かったので
何のトラブルもなくスムーズに第4問までやって来られた受験生は
決して多くはなかったと思います。ここまでやって来るのもしんどいのに
この問題もまた設問が多くて厄介だ

小問の途中でコロコロと設定を変えてきたり,
正しいものを選べ,みたいなややこしい設問入れてきたりと
なんとも意地悪な構成になっています。
時間内にちゃんと最後の問題に辿り着いた受験生は何人くらい居たのでしょう

 (1)1番
(1)1番
さっそく証明問題です。△ABP∽△AQBを示すのですが,
標準的な解法は頂角が共通であることと∠APB=∠ABQをいうことでしょう。
【証明】△ABPと△AQBにおいて
∠BAP=∠QAB (共通角) …
△ABCはAB=ACの二等辺三角形だから底角は等しいので
∠ABC=∠ACB
また,弧ABの円周角について ∠ACB=∠APB
従って,∠APB=∠ABQ …

 より,対応する2組の角がそれぞれ等しいので,△ABP∽△AQB (証明終)
より,対応する2組の角がそれぞれ等しいので,△ABP∽△AQB (証明終)
別解を作るとすれば例えば△ABQ∽△CPQ,△ACQ∽△BPQ,
△ACP∽△AQCなどを先に示して辺の比の関係などを求める
といった方法が思い浮かびますが,回りくどいです
【証明】△ACPと△AQCにおいて
∠CAP=∠QAC (共通角) …
△ABCはAB=ACの二等辺三角形だから底角は等しいので
∠ABC=∠ACB
また,弧ACの円周角について ∠ABC=∠APC
従って,∠APC=∠ACQ …

 より,対応する2組の角がそれぞれ等しいので,△ACP∽△AQC
より,対応する2組の角がそれぞれ等しいので,△ACP∽△AQC
このとき,AC:AQ=AP:AC
△ABPと△AQBにおいて
∠BAP=∠QAB (共通角) …
AB=ACより AB:AQ=AP:AB …

 より,対応する2組の辺の比とその間の角がそれぞれ等しいので
より,対応する2組の辺の比とその間の角がそれぞれ等しいので
△ABP∽△AQB (証明終)
 (1)2番
(1)2番
1番で証明した△ABP∽△AQBより従う AP:AB=AB:AQ
を使うのが手っ取り早いと思います

△ABP∽△AQBの方に着目しても良いでしょう。大した違いはありません。
しかし,それ以外で別解を作ろうと思うと意外と大変ですね
上記の方法で簡単に解けるシンプルな問題ですので,敢えて難しく解く必要も
ないのですが,様々な考え方を模索してみる作業は楽しいものですよ。
とりあえず△ABCは二等辺三角形なのでAからBCに垂線AHを下してみると
これは何かと役立ちそうです

例えばAQ=9k,QP=kとおいて,AQを別のkの式で表して
方程式を立てて解いてみます。


続いては,ちょっとズルい技を使って解いてみます。
図形問題において,与えられた条件を満たす図形が一意的に決定されるか
どうかというのは大事なポイントです。
この設問ではAB=AC=10とAQ:QC=9:1しか条件がないので
そのような条件を満たす図形というのはいくらでも考えられます。
そのようなどんな図形に対しても常にAQが一定の値を保つんだろうという
結果が予想できます。
それならば,自分に都合のいい条件を勝手に追加して問題を簡単にしてしまえ!
というズル技を使うことが出来ます。
今回はAPが直径になるという条件を勝手に追加してみます。
半径を5a,OQ=4a,QP=aとなるような特別の場合を想定し
図を描いてみると確かにAQ:QP=9:1になっています。
この状況下では前の設問で求めた相似関係を使うことなく答えが求められます。

ただし,これはあくまでズル技です。答えを求める分には結構使える手ですが
記述式の答案では満点はもらえないです
あくまで勝手に条件を追加した1つの特殊な場合においてはAQ=3√10になりますよ~ってことが分かっただけで,
条件を変えても常にAQ=3√10が成り立つことは何も説明できていません
高校数学になると記述式の答案を書くことになりますが,必要十分性の議論で減点されるということはよくあることです。
 (2)1番
(2)1番

正しいものを選べ,などという意地悪な形式の出題です。
4択なんてセンター試験みたい
1個1個検証してくのは結構大変です。しかもよりによって最後のエが答えだし!
素直にAB^2=AQ×APを証明せよ。の方が手がつけやすいもんですが~。
恐らくはどっかの三角形の相似関係から導かれる関係式が正解なんだと思われます。
では,相似な三角形を挙げてみましょう。
△ABQ∽△APB △ADP∽△BDC △ABD∽△PCD
後半2つの相似関係は円に内接する四角形ならいつも出てきます。
というわけで最初の△ABQ∽△APBが怪しいですね。
AB:AP=AQ:ABが成り立つので AB^2=AQ×AP が
でてきました! めでたしめでたし
めでたしめでたし

…という風に始めから目星をつけてやるのが手堅いやり方かな?
さっきみたいに勝手に条件を追加して特殊な場合を想定するのも良いでしょう。
少なくともア~エのうち,その特殊な場合で成り立たない選択肢はハズレなわけです。
そんなわけで△ABCが1辺2の正三角形でしかもAP⊥ACという場合を考えます。

このとき各辺の長さが全部すぐに計算できてしまうので,
あとはア~エのうちどれが成り立ってどれが成り立たないか見てみれば
良いわけであります。
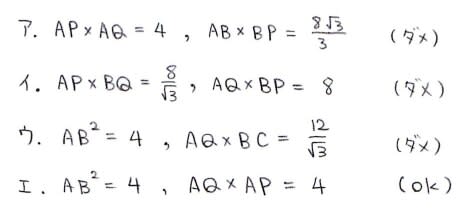
成り立つのはエだけなので,答えはエで決まりです♪
ちょっと卑怯ですけどね
ちなみにもし成り立つ選択肢が複数あった場合は,
常に正しいからそれが成立したのか,たまたま偶然なのか分からないので
別の特殊な状況を考えてみるなどすればよいでしょう。
なんだか長くなってきたので,後半戦は次回にまわすことにします
ではでは~
前回に引き続いて今年の春の長野県の公立入試問題を取り上げますね

今回取り扱うのは最後の大問である第4問です。
円や相似が絡んだ入試問題鉄板の図形問題です。
問題と解答はこちらから見られます。
http://www.pref.nagano.lg.jp/kyouiku/kyougaku/koukounuusi/index24.htm
前回も述べたように,全体的に難易度が高く問題数も非常に多かったので
何のトラブルもなくスムーズに第4問までやって来られた受験生は
決して多くはなかったと思います。ここまでやって来るのもしんどいのに
この問題もまた設問が多くて厄介だ


小問の途中でコロコロと設定を変えてきたり,
正しいものを選べ,みたいなややこしい設問入れてきたりと
なんとも意地悪な構成になっています。
時間内にちゃんと最後の問題に辿り着いた受験生は何人くらい居たのでしょう


 (1)1番
(1)1番さっそく証明問題です。△ABP∽△AQBを示すのですが,
標準的な解法は頂角が共通であることと∠APB=∠ABQをいうことでしょう。
【証明】△ABPと△AQBにおいて
∠BAP=∠QAB (共通角) …

△ABCはAB=ACの二等辺三角形だから底角は等しいので
∠ABC=∠ACB
また,弧ABの円周角について ∠ACB=∠APB
従って,∠APB=∠ABQ …


 より,対応する2組の角がそれぞれ等しいので,△ABP∽△AQB (証明終)
より,対応する2組の角がそれぞれ等しいので,△ABP∽△AQB (証明終)別解を作るとすれば例えば△ABQ∽△CPQ,△ACQ∽△BPQ,
△ACP∽△AQCなどを先に示して辺の比の関係などを求める
といった方法が思い浮かびますが,回りくどいです

【証明】△ACPと△AQCにおいて
∠CAP=∠QAC (共通角) …

△ABCはAB=ACの二等辺三角形だから底角は等しいので
∠ABC=∠ACB
また,弧ACの円周角について ∠ABC=∠APC
従って,∠APC=∠ACQ …


 より,対応する2組の角がそれぞれ等しいので,△ACP∽△AQC
より,対応する2組の角がそれぞれ等しいので,△ACP∽△AQCこのとき,AC:AQ=AP:AC
△ABPと△AQBにおいて
∠BAP=∠QAB (共通角) …

AB=ACより AB:AQ=AP:AB …


 より,対応する2組の辺の比とその間の角がそれぞれ等しいので
より,対応する2組の辺の比とその間の角がそれぞれ等しいので△ABP∽△AQB (証明終)
 (1)2番
(1)2番1番で証明した△ABP∽△AQBより従う AP:AB=AB:AQ
を使うのが手っ取り早いと思います


△ABP∽△AQBの方に着目しても良いでしょう。大した違いはありません。
しかし,それ以外で別解を作ろうと思うと意外と大変ですね

上記の方法で簡単に解けるシンプルな問題ですので,敢えて難しく解く必要も
ないのですが,様々な考え方を模索してみる作業は楽しいものですよ。
とりあえず△ABCは二等辺三角形なのでAからBCに垂線AHを下してみると
これは何かと役立ちそうです


例えばAQ=9k,QP=kとおいて,AQを別のkの式で表して
方程式を立てて解いてみます。


続いては,ちょっとズルい技を使って解いてみます。
図形問題において,与えられた条件を満たす図形が一意的に決定されるか
どうかというのは大事なポイントです。
この設問ではAB=AC=10とAQ:QC=9:1しか条件がないので
そのような条件を満たす図形というのはいくらでも考えられます。
そのようなどんな図形に対しても常にAQが一定の値を保つんだろうという
結果が予想できます。
それならば,自分に都合のいい条件を勝手に追加して問題を簡単にしてしまえ!

というズル技を使うことが出来ます。
今回はAPが直径になるという条件を勝手に追加してみます。
半径を5a,OQ=4a,QP=aとなるような特別の場合を想定し
図を描いてみると確かにAQ:QP=9:1になっています。
この状況下では前の設問で求めた相似関係を使うことなく答えが求められます。

ただし,これはあくまでズル技です。答えを求める分には結構使える手ですが
記述式の答案では満点はもらえないです

あくまで勝手に条件を追加した1つの特殊な場合においてはAQ=3√10になりますよ~ってことが分かっただけで,
条件を変えても常にAQ=3√10が成り立つことは何も説明できていません

高校数学になると記述式の答案を書くことになりますが,必要十分性の議論で減点されるということはよくあることです。
 (2)1番
(2)1番
正しいものを選べ,などという意地悪な形式の出題です。
4択なんてセンター試験みたい

1個1個検証してくのは結構大変です。しかもよりによって最後のエが答えだし!
素直にAB^2=AQ×APを証明せよ。の方が手がつけやすいもんですが~。
恐らくはどっかの三角形の相似関係から導かれる関係式が正解なんだと思われます。
では,相似な三角形を挙げてみましょう。
△ABQ∽△APB △ADP∽△BDC △ABD∽△PCD
後半2つの相似関係は円に内接する四角形ならいつも出てきます。
というわけで最初の△ABQ∽△APBが怪しいですね。
AB:AP=AQ:ABが成り立つので AB^2=AQ×AP が
でてきました!
 めでたしめでたし
めでたしめでたし

…という風に始めから目星をつけてやるのが手堅いやり方かな?
さっきみたいに勝手に条件を追加して特殊な場合を想定するのも良いでしょう。
少なくともア~エのうち,その特殊な場合で成り立たない選択肢はハズレなわけです。
そんなわけで△ABCが1辺2の正三角形でしかもAP⊥ACという場合を考えます。

このとき各辺の長さが全部すぐに計算できてしまうので,
あとはア~エのうちどれが成り立ってどれが成り立たないか見てみれば
良いわけであります。
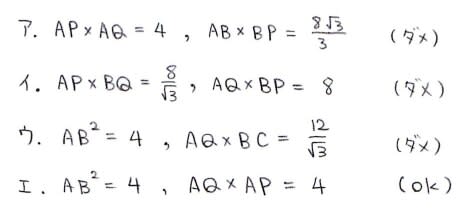
成り立つのはエだけなので,答えはエで決まりです♪
ちょっと卑怯ですけどね

ちなみにもし成り立つ選択肢が複数あった場合は,
常に正しいからそれが成立したのか,たまたま偶然なのか分からないので
別の特殊な状況を考えてみるなどすればよいでしょう。
なんだか長くなってきたので,後半戦は次回にまわすことにします

ではでは~















※コメント投稿者のブログIDはブログ作成者のみに通知されます