推測統計学びの準備(確率)について復習しています。ここでいう確率とは サンプルの抽出方法に「無作為抽出」方法があることを知りました。
このレポートを より理解するには 野球球団を母集団に例えて 「某野球球団の・ストライクゾーン 0123456789 記録」と読み替え イメージしてみては 如何でしょうか。さらに無作為試行(A選手・B選手・C選手・・・・・・)の実績を把握することで 球団の全体を評価していいのでしょうか・・・という学びの復習です。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
その無作為方法で 抽出した 分析の 結果のデータは どの程度信頼してよいか疑問がわきますね、
つまり分析結果レポートの中に 「 P値 」欄があります これは何を意味するのか興味がわきました。
まずは私(猿)の 過去の提出した学びのレポートをご覧ください。

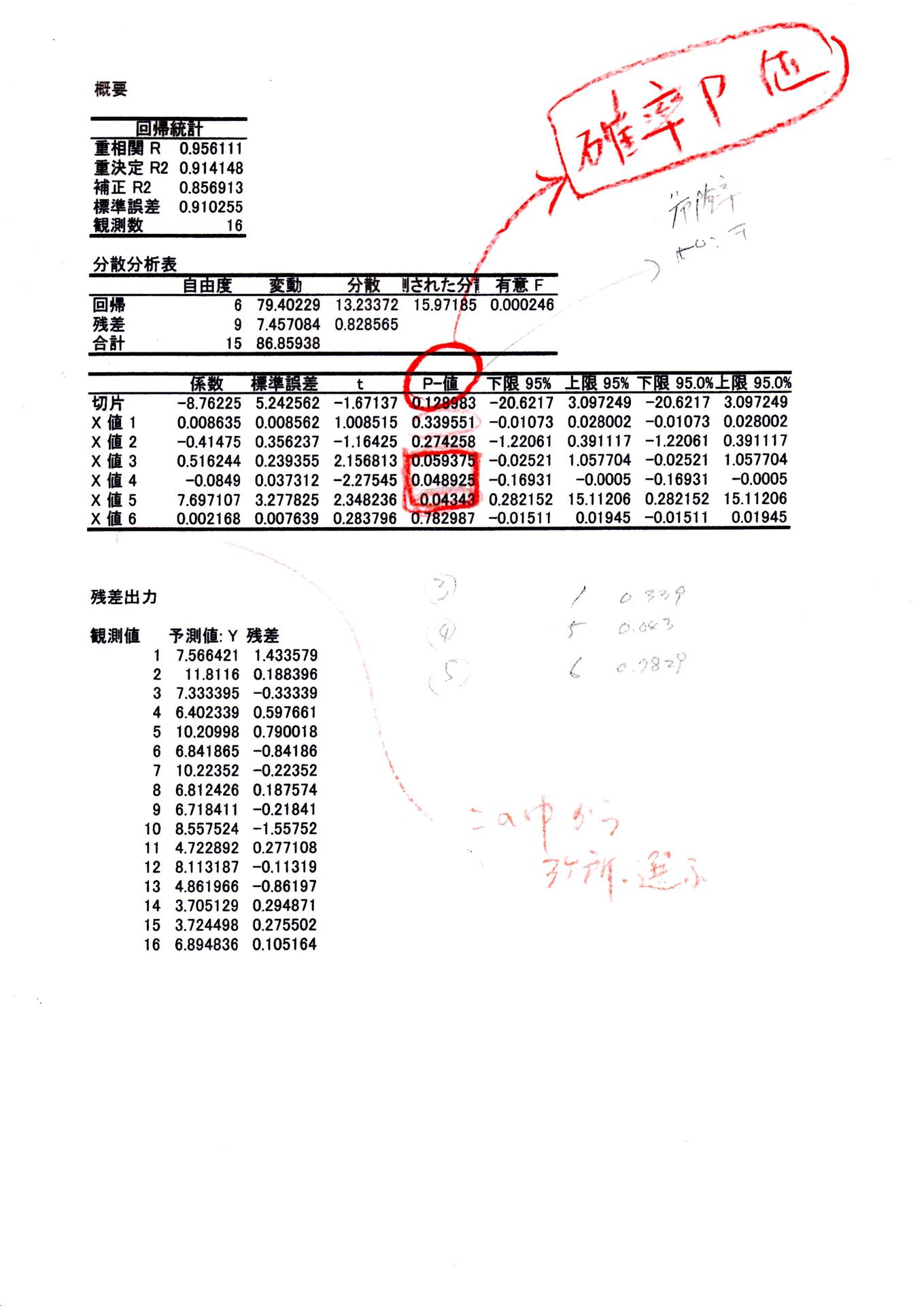
①回帰統計・・・P値欄を確認ください・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・
②無作為抽出する上で 考慮したい 母集団の本質を真実に把握する必要があります。しかし統計学では 100%言い当てる事は求めていないようで、そこで「P値」で信頼度を数値化していることが解りました。
①の資料で P値は パンチ とも言い パンチは 0.05以上は危険であり 信頼できないと解釈しています、パンチを受けるなら、P=0.048 P=0.043のように 小さいほうが良い と記憶していれば役に立つでしょう.
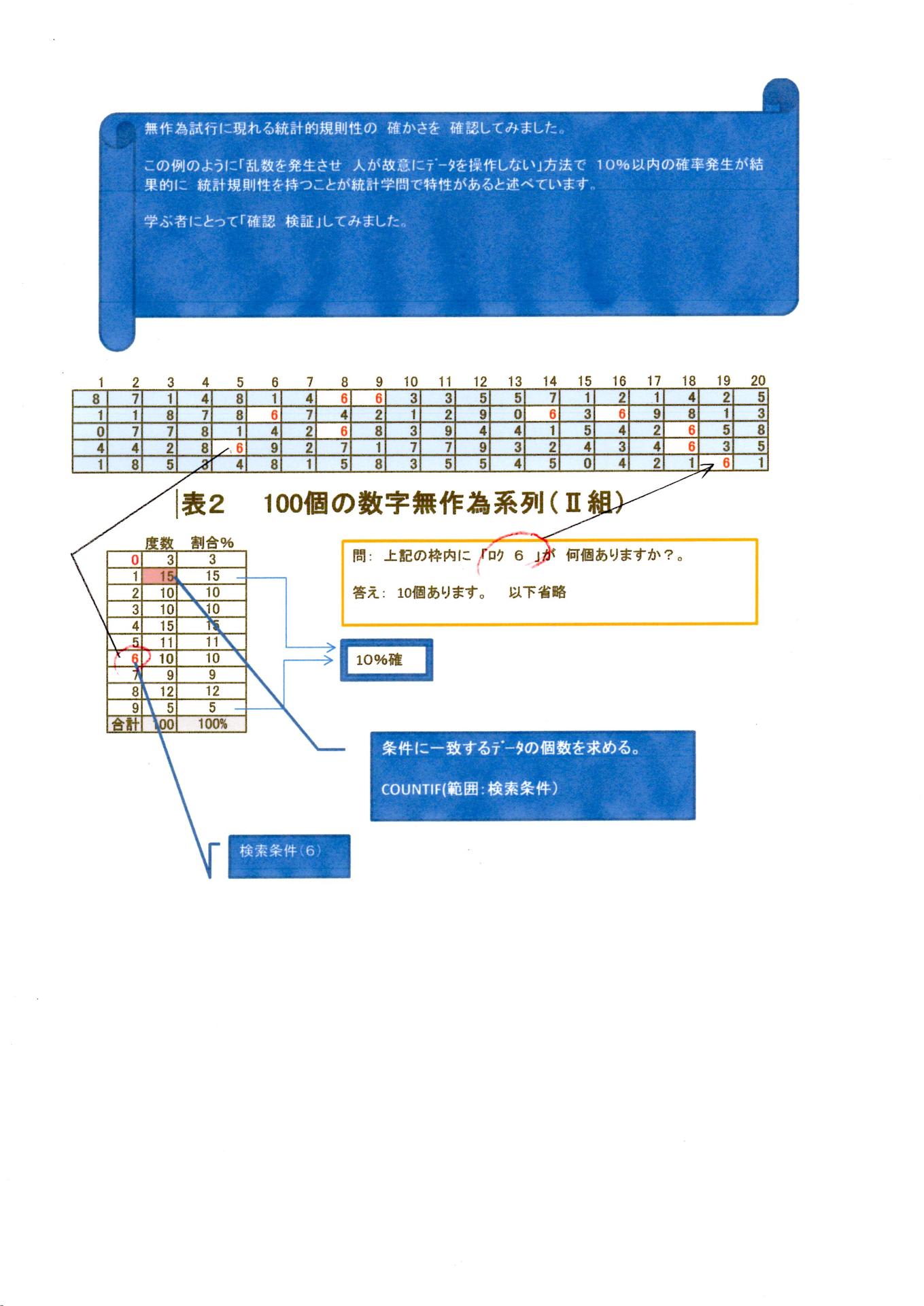
③では実際に検証してみました。 別紙の表1は 乱数を発生させて 「0 から 9」までを無作為に発生しています。 この表の中に 0は6個 1は14個 ・・・・9は5個 の表を作成しました。表中9最小値=5%であり 表中1最大=14%となりました、この出現率の誤差は(14-5=9%)であることが解りました。
統計学では 無作為に標本を抽出すれば 解は 10%以内であることを定義つけしてあります。これの説明を言い換えると誤差は10%以内に収まることを知りました。母集団を診察するにあたり標本誤差が少ないほうが良いことになります。
別紙1の標本ダミーをご覧ください
拡大レポートです。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
別紙2をご覧ください。別紙1に類似しています。

・・・・・・・・・・・・・・・・・・・・・・・・・・
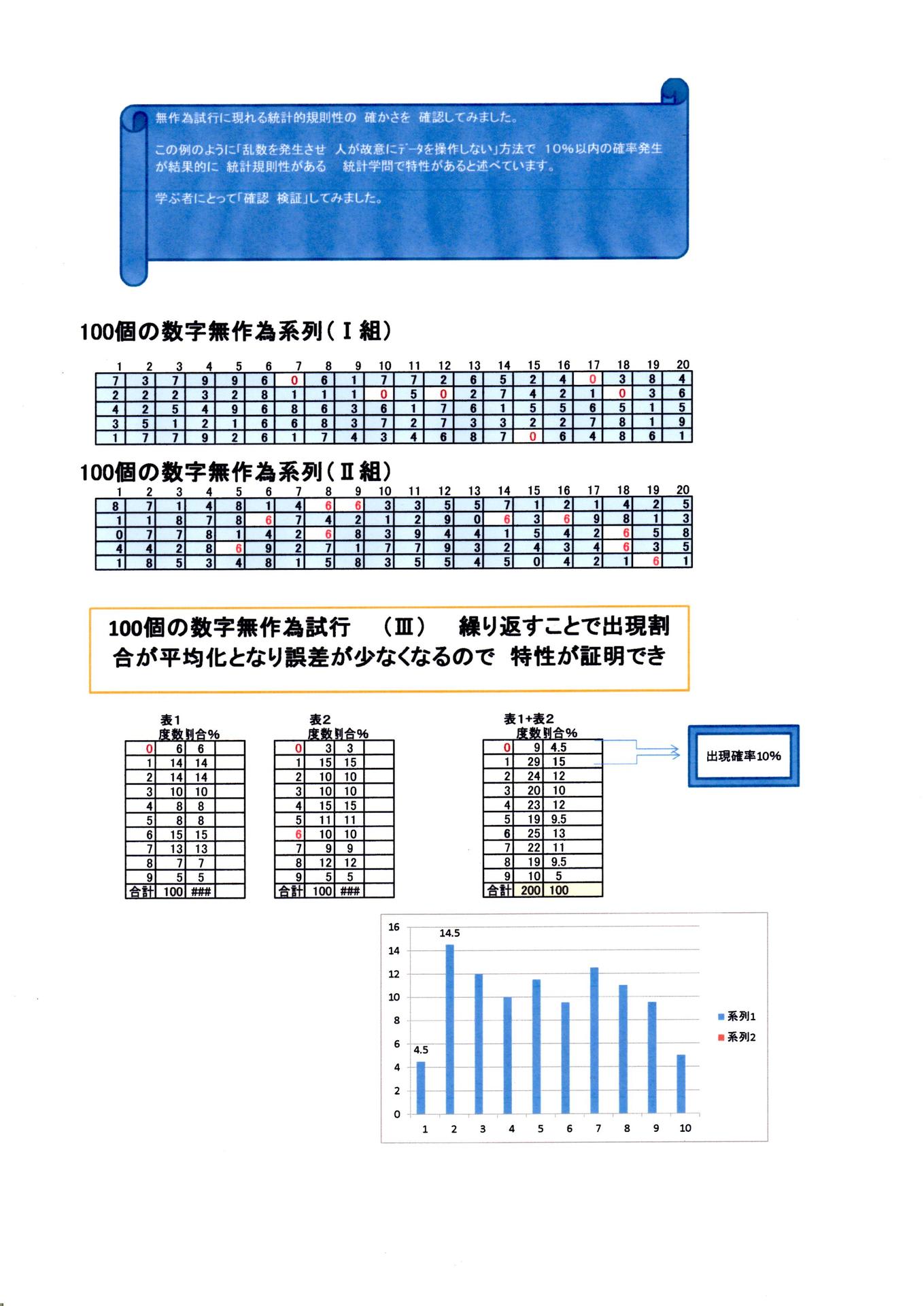
さらに別紙3をご覧ください これは 無作為Ⅰ プラス 無作為Ⅱ の表を合成した例題です。いずれも別紙1・別紙Ⅱ・別紙Ⅲ いずれの例題も 最小最大割合の誤差は 10%以内にあります。
母集団から抜き取られる サンプルの割合 誤差は 少ないほうが良いわけである。
別紙3をご覧ください。

拡大レポートをご覧ください。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・
無作為に 抽選に参加するとすれば サイコロ方式 又は トランプ方式 で占う どちらにしますか、以上確率はどちらが良いでしょうか。
標本抽出にあっては「無作為」に関して 概要を深めたい又学びたい読者様には 書店に販売しています 図書p70を参照ください 漫画ふうになっていて 良く解る本です。

以上 記述は 統計の猿でした。
・・・
このレポートを より理解するには 野球球団を母集団に例えて 「某野球球団の・ストライクゾーン 0123456789 記録」と読み替え イメージしてみては 如何でしょうか。さらに無作為試行(A選手・B選手・C選手・・・・・・)の実績を把握することで 球団の全体を評価していいのでしょうか・・・という学びの復習です。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
その無作為方法で 抽出した 分析の 結果のデータは どの程度信頼してよいか疑問がわきますね、
つまり分析結果レポートの中に 「 P値 」欄があります これは何を意味するのか興味がわきました。
まずは私(猿)の 過去の提出した学びのレポートをご覧ください。

①回帰統計・・・P値欄を確認ください・・・・


・・・・・・・・・・・・・・・・・・・・・・・・・・・
②無作為抽出する上で 考慮したい 母集団の本質を真実に把握する必要があります。しかし統計学では 100%言い当てる事は求めていないようで、そこで「P値」で信頼度を数値化していることが解りました。
①の資料で P値は パンチ とも言い パンチは 0.05以上は危険であり 信頼できないと解釈しています、パンチを受けるなら、P=0.048 P=0.043のように 小さいほうが良い と記憶していれば役に立つでしょう.
③では実際に検証してみました。 別紙の表1は 乱数を発生させて 「0 から 9」までを無作為に発生しています。 この表の中に 0は6個 1は14個 ・・・・9は5個 の表を作成しました。表中9最小値=5%であり 表中1最大=14%となりました、この出現率の誤差は(14-5=9%)であることが解りました。
統計学では 無作為に標本を抽出すれば 解は 10%以内であることを定義つけしてあります。これの説明を言い換えると誤差は10%以内に収まることを知りました。母集団を診察するにあたり標本誤差が少ないほうが良いことになります。
別紙1の標本ダミーをご覧ください

拡大レポートです。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
別紙2をご覧ください。別紙1に類似しています。


・・・・・・・・・・・・・・・・・・・・・・・・・・
さらに別紙3をご覧ください これは 無作為Ⅰ プラス 無作為Ⅱ の表を合成した例題です。いずれも別紙1・別紙Ⅱ・別紙Ⅲ いずれの例題も 最小最大割合の誤差は 10%以内にあります。
母集団から抜き取られる サンプルの割合 誤差は 少ないほうが良いわけである。
別紙3をご覧ください。

拡大レポートをご覧ください。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・
無作為に 抽選に参加するとすれば サイコロ方式 又は トランプ方式 で占う どちらにしますか、以上確率はどちらが良いでしょうか。
標本抽出にあっては「無作為」に関して 概要を深めたい又学びたい読者様には 書店に販売しています 図書p70を参照ください 漫画ふうになっていて 良く解る本です。

以上 記述は 統計の猿でした。
・・・









