
「数学 その形式と機能: ソーンダース・マックレーン」
内容紹介:
数多くの名著の著者として著名なマックレーン教授が、現代数学の各部門にわたってその基礎概念を縦横に論じたもの。数学の構造、性格、および各部門の関係を数学と哲学の両面から論じ、数学の起原から現代数学までを概観しながら、それぞれの問題の本質を明らかにした。現代数学全般に精通した原著者のライフワーク。
1992年4月刊行、621ページ。
著者について:
ソーンダース・マックレーン
1909年8月4日、米国タフトヴィル生まれ。1934年、ゲッティンゲン大学でP.ベルナイスの指導を受け論理学に関する論文で博士号を取得。1947年よりシカゴ大学教授、1982年より同大学名誉教授。またMAA会長(1951‐52)、AMS会長(1973‐74)を歴任。2005年4月14日、米国サンフランシスコにて歿。
理数系書籍のレビュー記事は本書で324冊目。
本書は「数学とは何か(原書第2版):R.クーラント、H.ロビンズ、I.スチュアート」を書いたときに読者の方からご紹介いただいた本だ。ようやく読み終えることができた。この2冊のテーマは同じだが「数学とは何か」が幾何学系に話題が偏っているのに対し、本書は解析学、幾何学、数論、代数のバランスがとれているという印象を持った。数学全体を俯瞰するのならば本書のほうがよいと思う。
章立ては次のとおり。
第1章:形式的構造の起源
第2章:整数から有理数へ
第3章:幾何学
第4章:実数
第5章:関数、変換および群
第6章:微積分学の諸概念
第7章:線形代数
第8章:空間が有する形式
第9章:力学
第10章:複素解析とトポロジー
第11章:集合、論理、圏
第12章:数学のネットワーク
まず本書が想定している読者だが、大学の学部レベルの数学を一通り学んだ学生向けということだろう。数学全体を俯瞰しているとはいえ学部1、2年生には難しすぎるし、まして「数学やり直し系」の本ではない。学部1、2年生が数学全体を俯瞰するのなら本書よりも「『数学ガイダンス2016』数学セミナー増刊:日本評論社」のほうがずっとよい。
第1章から第10章までは各分野の概要と他の分野とのつながりを解説する。教科書のように厳密な証明をせずに進めるから1冊であらゆる分野をカバーできるのだ。けれども全く学んでいない人にとっては何を言っているのかわからない。つまり学ぶための本ではないということ。
また、僕のように各分野をひととおり学んだ者にとっては知っていることばかりでかなり退屈なのも事実。筋道立てて進めるためには高校数学レベルの話も含めておかなければならないからだ。数学全体をカバーする本を書くのは難しいことだと気付かせられた。対象読者を絞るのが難しいからだ。
退屈しながらも読み進めることができたのは、各章の終わりに「他の分野とのつながり」が詳しく示されているからである。これは分野別の教科書では知ることができない内容だ。これまでの学習経験で培われてきたこと、おぼろげながら「数学の全体はこのような感じに結びついているのだ」という印象を、著者の言葉であらためて解説されると「なるほどなぁ。」と納得させられるのである。幾何学、解析学、代数学、物理学のつながりが、読み進めるにしたがって明らかになっていく。
特に第8章の解析力学のラグランジュ方程式からハミルトン方程式への変換が、数学では接空間から余接空間への変換に対応するのだということを著者が発見したという解説がとても興味深かった。この部分は数式による詳しい導出が行われているのでじっくり読んだほうがよい。
僕が萌え始めたのは「第10章:複素解析とトポロジー」あたりから。解析接続やリーマン面の説明はこの上なくわかりやすく、なぜ重要なのかがよく理解できた。
「第11章:集合、論理、圏」は数学基礎論の話。何を数学全体の土台とすべきかということだ。集合論ではなぜダメなのかがよくわかる。集合論では緩すぎるし、基礎とする公理の取り方で異なる体系が生まれてしまう。大ざっぱに言えば砂上の楼閣なのだ。集合論に置き換わる土台としての圏論の有用性や圏論と集合論の関係性がよく理解できた。著者による「圏論の基礎」をお読みになる前にこの章であらましを知っておくとよいだろう。
「第12章:数学のネットワーク」で本書全体を総括する。幾何学、代数学、解析学、数論と物理だけでなく応用数学にも話は拡がり、「数学とは何か?」や「数学はどのように発展してきたのか?」がプラトニズムまで遡って語られる。
「数学とは発見なのか?それとも創造なのか?」という問いにも著者はご自身の回答を示されている。初学者には芽や層などの概念は人為的に設定されたもの、創造されたものに思われがちだが、現代数学の諸分野に通じた著者のような人から見ると、それらの概念は他の分野とのつながりが明らかで、抽象的でより高い立場から見るとその実在性がはっきりと感じられるのだという。つまり著者にとって「数学は発見するもの」なのである。
数学の発展をもたらすものは一般化と抽象化であるという。著者はこの2つの言葉を明確に区別している。一般化とはすでに知られているいくつかの特定の結果がより、一般的な1個の定理にまとめられるような場合で、個々の直角三角形についての考察からピタゴラスの定理が生まれ、さらにピタゴラスの定理を満たす整数解を得るためのアルゴリズムが発展するようなことだ。
抽象化とはすでに知られている結果の中心的側面にのみ注目し、より新しく混じりけのない数学の概念の記述と分析をするものだ。抽象化には「削除による抽象化」、「類推による抽象化」、「考察の焦点の移動による抽象化」などのタイプがあり、それぞれについて例をあげている。
アマゾンのレビュー記事に「二十世紀後半の重要な部分、コホモロジーやファイバー束・接続の理論(ゲージ理論)にもっとほんの少し触れるだけでなく本格的に論じて欲しかったと思う。」という感想があった。概ね僕も同様に感じた。しかし本書の原書が出版されたのは1986年である。「ゲージ理論とトポロジーの年表」という記事で書いたように1986年以降にゲージ理論と数学のつながりはよりいっそう強いものであることがわかってきたのだ。「数学の統一理論」としてのラングランズ・プログラムもこの時代には部分的に明らかにされているに過ぎない。本書が書かれた時代を考慮して読むべきなのだろう。
本書のテーマと直接かかわるわけではないが、「四色定理」や「ポアンカレ予想」、「フェルマーの最終定理」が証明されたのは本書が書かれた後のことである。
本書に掲載されている図版はどれも示唆に富むものだが、特に以下の4つを紹介しておこう。

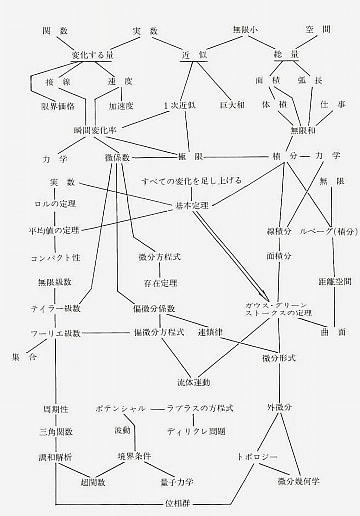


翻訳の元になった原書はこちらである。
「Mathematics Form and Function: Saunders MacLane」(ハードカバー)

関連記事:
数学とは何か(原書第2版):R.クーラント、H.ロビンズ、I.スチュアート
https://blog.goo.ne.jp/ktonegaw/e/e2b02a51b73a9716b077da16a102aaff
数学とは何か―アティヤ 科学・数学論集
https://blog.goo.ne.jp/ktonegaw/e/b3ce277f0624f0adea8186a0168bcf99
数学の大統一に挑む:エドワード・フレンケル
https://blog.goo.ne.jp/ktonegaw/e/43ca100e56e15427613b009af55c8f7d
無限をつかむ: イアン・スチュアートの数学物語
https://blog.goo.ne.jp/ktonegaw/e/2307174ab3fd537695b1287f059f2304
大学で学ぶ数学とは(概要編)
https://blog.goo.ne.jp/ktonegaw/e/07137c47d16d95ddde8f5c4cb6f37d55
圏論の歩き方(日本評論社)
https://blog.goo.ne.jp/ktonegaw/e/2c0ccc6e7ec3776e77dce337a11f0078
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。







「数学 その形式と機能: ソーンダース・マックレーン」

日本語版への序文
監修者のことば
原序
序説
第1章:形式的構造の起源
- 自然数
- 無限集合
- 置換
- 時刻と順序
- 空間と運動
- 対称性
- 変換群
- 群
- ブール代数
- 微積分学、連続性および位相
- 人間活動とアイデア
- 数学上の諸活動
- 公理的構造
第2章:整数から有理数へ
- 自然数の諸性質
- ペアノの(Peano)の公準
- 帰納定理により記述される自然数
- 数論
- 整数
- 有理数
- 合同式
- 基数
- 順序数
- 数(自然数)とは何か?
第3章:幾何学
- 空間にかかわる諸活動
- 図を使わない証明
- 平行線の公理
- 双曲幾何学
- 楕円幾何学
- 幾何学的量
- 向き付け
- 幾何学における群
- 立体幾何学
- 幾何学は科学であるか?
第4章:実数
- 大きさの測定
- 幾何学的量としての大きさ
- 大きさの操作(演算)
- 大きさの比較
- 実数の公理
- 実数の算術的構成
- ベクトル幾何学
- 解析幾何学
- 三角法
- 複素数
- 立体射影と無限遠点
- 虚数は現実のものか?
- 抽象代数登場
- 四元数その他
- 要約
第5章:関数、変換および群
- 関数のタイプ
- 写像
- 関数とは何か
- 対の集合としての関数
- 変換群
- ガロア理論
- 群の構成
- 単純群
- 要約:像と合成という考え方
第6章:微積分学の諸概念
- 起源
- 積分法
- 微分係数、導関数
- 積分法の基本定理
- ケプラー(Kepler)の法則とニュートンの法則
- 微分方程式
- 微積分学の基礎づけ
- テイラー(Taylor)級数と近似
- 偏導関数、偏微分係数
- 微分形式
- 微積分学から解析学へ
- 諸概念のあいだの内部関連
第7章:線形代数
- 線形性の源泉
- 線形変換と行列
- 固有値
- 双対空間
- 内積空間
- 直交行列
- 随伴変換
- 主軸定理
- 双線形性とテンソル積
- 商空間
- 外積代数と微分形式
- 相似性と直和
- 要約
第8章:空間が有する形式
- 曲率
- 曲面のガウス曲率
- 弧長と内在的幾何学
- 多価関数とリーマン面
- 多様体の例
- 滑らかな多様体
- 径路と量
- リーマン計量
- 層
- 幾何学とは何か?
第9章:力学
- ケプラーの法則
- 運動量、仕事、エネルギー
- ラグランジュの方程式
- 速度と接束
- 数学における力学
- ハミルトンの原理
- ハミルトンの方程式
- トリックとアイデア
- 主関数
- ハミルトン-ヤコビの方程式
- 回転ごま
- 力学の形式
- 量子力学
第10章:複素解析とトポロジー
- 1変数複素関数
- 病的関数
- 複素微分
- 複素積分
- 平面上の径路
- コーシーの定理
- 一様収束
- 冪(べき)級数
- コーシーの積分公式
- 特異点
- リーマン面
- 芽と層
- 解析学、幾何学、位相数学
第11章:集合、論理、圏
- 集合の階層
- 公理的集合論
- 命題計算
- 第1階の言語
- 述語計算
- 正確な推論と理解
- ゲーデルの不完全性定理
- 独立性の証明
- 圏と関手
- 自然変換
- 普遍性
- 写像の公理
- 直観主義の論理
- 層の方法による独立性の証明
- 基礎付けか組織化か?
第12章:数学のネットワーク
- 形式性
- アイデア
- ネットワーク
- 部門、分野および下位区分
- 問題
- 数学を理解するということ
- 一般化と抽象化
- 新機軸
- 数学は真実か?
- プラトニズム
- 好ましい研究の方向
- 要約
参考文献
記号一覧
訳者あとがき
索引
内容紹介:
数多くの名著の著者として著名なマックレーン教授が、現代数学の各部門にわたってその基礎概念を縦横に論じたもの。数学の構造、性格、および各部門の関係を数学と哲学の両面から論じ、数学の起原から現代数学までを概観しながら、それぞれの問題の本質を明らかにした。現代数学全般に精通した原著者のライフワーク。
1992年4月刊行、621ページ。
著者について:
ソーンダース・マックレーン
1909年8月4日、米国タフトヴィル生まれ。1934年、ゲッティンゲン大学でP.ベルナイスの指導を受け論理学に関する論文で博士号を取得。1947年よりシカゴ大学教授、1982年より同大学名誉教授。またMAA会長(1951‐52)、AMS会長(1973‐74)を歴任。2005年4月14日、米国サンフランシスコにて歿。
理数系書籍のレビュー記事は本書で324冊目。
本書は「数学とは何か(原書第2版):R.クーラント、H.ロビンズ、I.スチュアート」を書いたときに読者の方からご紹介いただいた本だ。ようやく読み終えることができた。この2冊のテーマは同じだが「数学とは何か」が幾何学系に話題が偏っているのに対し、本書は解析学、幾何学、数論、代数のバランスがとれているという印象を持った。数学全体を俯瞰するのならば本書のほうがよいと思う。
章立ては次のとおり。
第1章:形式的構造の起源
第2章:整数から有理数へ
第3章:幾何学
第4章:実数
第5章:関数、変換および群
第6章:微積分学の諸概念
第7章:線形代数
第8章:空間が有する形式
第9章:力学
第10章:複素解析とトポロジー
第11章:集合、論理、圏
第12章:数学のネットワーク
まず本書が想定している読者だが、大学の学部レベルの数学を一通り学んだ学生向けということだろう。数学全体を俯瞰しているとはいえ学部1、2年生には難しすぎるし、まして「数学やり直し系」の本ではない。学部1、2年生が数学全体を俯瞰するのなら本書よりも「『数学ガイダンス2016』数学セミナー増刊:日本評論社」のほうがずっとよい。
第1章から第10章までは各分野の概要と他の分野とのつながりを解説する。教科書のように厳密な証明をせずに進めるから1冊であらゆる分野をカバーできるのだ。けれども全く学んでいない人にとっては何を言っているのかわからない。つまり学ぶための本ではないということ。
また、僕のように各分野をひととおり学んだ者にとっては知っていることばかりでかなり退屈なのも事実。筋道立てて進めるためには高校数学レベルの話も含めておかなければならないからだ。数学全体をカバーする本を書くのは難しいことだと気付かせられた。対象読者を絞るのが難しいからだ。
退屈しながらも読み進めることができたのは、各章の終わりに「他の分野とのつながり」が詳しく示されているからである。これは分野別の教科書では知ることができない内容だ。これまでの学習経験で培われてきたこと、おぼろげながら「数学の全体はこのような感じに結びついているのだ」という印象を、著者の言葉であらためて解説されると「なるほどなぁ。」と納得させられるのである。幾何学、解析学、代数学、物理学のつながりが、読み進めるにしたがって明らかになっていく。
特に第8章の解析力学のラグランジュ方程式からハミルトン方程式への変換が、数学では接空間から余接空間への変換に対応するのだということを著者が発見したという解説がとても興味深かった。この部分は数式による詳しい導出が行われているのでじっくり読んだほうがよい。
僕が萌え始めたのは「第10章:複素解析とトポロジー」あたりから。解析接続やリーマン面の説明はこの上なくわかりやすく、なぜ重要なのかがよく理解できた。
「第11章:集合、論理、圏」は数学基礎論の話。何を数学全体の土台とすべきかということだ。集合論ではなぜダメなのかがよくわかる。集合論では緩すぎるし、基礎とする公理の取り方で異なる体系が生まれてしまう。大ざっぱに言えば砂上の楼閣なのだ。集合論に置き換わる土台としての圏論の有用性や圏論と集合論の関係性がよく理解できた。著者による「圏論の基礎」をお読みになる前にこの章であらましを知っておくとよいだろう。
「第12章:数学のネットワーク」で本書全体を総括する。幾何学、代数学、解析学、数論と物理だけでなく応用数学にも話は拡がり、「数学とは何か?」や「数学はどのように発展してきたのか?」がプラトニズムまで遡って語られる。
「数学とは発見なのか?それとも創造なのか?」という問いにも著者はご自身の回答を示されている。初学者には芽や層などの概念は人為的に設定されたもの、創造されたものに思われがちだが、現代数学の諸分野に通じた著者のような人から見ると、それらの概念は他の分野とのつながりが明らかで、抽象的でより高い立場から見るとその実在性がはっきりと感じられるのだという。つまり著者にとって「数学は発見するもの」なのである。
数学の発展をもたらすものは一般化と抽象化であるという。著者はこの2つの言葉を明確に区別している。一般化とはすでに知られているいくつかの特定の結果がより、一般的な1個の定理にまとめられるような場合で、個々の直角三角形についての考察からピタゴラスの定理が生まれ、さらにピタゴラスの定理を満たす整数解を得るためのアルゴリズムが発展するようなことだ。
抽象化とはすでに知られている結果の中心的側面にのみ注目し、より新しく混じりけのない数学の概念の記述と分析をするものだ。抽象化には「削除による抽象化」、「類推による抽象化」、「考察の焦点の移動による抽象化」などのタイプがあり、それぞれについて例をあげている。
アマゾンのレビュー記事に「二十世紀後半の重要な部分、コホモロジーやファイバー束・接続の理論(ゲージ理論)にもっとほんの少し触れるだけでなく本格的に論じて欲しかったと思う。」という感想があった。概ね僕も同様に感じた。しかし本書の原書が出版されたのは1986年である。「ゲージ理論とトポロジーの年表」という記事で書いたように1986年以降にゲージ理論と数学のつながりはよりいっそう強いものであることがわかってきたのだ。「数学の統一理論」としてのラングランズ・プログラムもこの時代には部分的に明らかにされているに過ぎない。本書が書かれた時代を考慮して読むべきなのだろう。
本書のテーマと直接かかわるわけではないが、「四色定理」や「ポアンカレ予想」、「フェルマーの最終定理」が証明されたのは本書が書かれた後のことである。
本書に掲載されている図版はどれも示唆に富むものだが、特に以下の4つを紹介しておこう。




翻訳の元になった原書はこちらである。
「Mathematics Form and Function: Saunders MacLane」(ハードカバー)

関連記事:
数学とは何か(原書第2版):R.クーラント、H.ロビンズ、I.スチュアート
https://blog.goo.ne.jp/ktonegaw/e/e2b02a51b73a9716b077da16a102aaff
数学とは何か―アティヤ 科学・数学論集
https://blog.goo.ne.jp/ktonegaw/e/b3ce277f0624f0adea8186a0168bcf99
数学の大統一に挑む:エドワード・フレンケル
https://blog.goo.ne.jp/ktonegaw/e/43ca100e56e15427613b009af55c8f7d
無限をつかむ: イアン・スチュアートの数学物語
https://blog.goo.ne.jp/ktonegaw/e/2307174ab3fd537695b1287f059f2304
大学で学ぶ数学とは(概要編)
https://blog.goo.ne.jp/ktonegaw/e/07137c47d16d95ddde8f5c4cb6f37d55
圏論の歩き方(日本評論社)
https://blog.goo.ne.jp/ktonegaw/e/2c0ccc6e7ec3776e77dce337a11f0078
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。




「数学 その形式と機能: ソーンダース・マックレーン」

日本語版への序文
監修者のことば
原序
序説
第1章:形式的構造の起源
- 自然数
- 無限集合
- 置換
- 時刻と順序
- 空間と運動
- 対称性
- 変換群
- 群
- ブール代数
- 微積分学、連続性および位相
- 人間活動とアイデア
- 数学上の諸活動
- 公理的構造
第2章:整数から有理数へ
- 自然数の諸性質
- ペアノの(Peano)の公準
- 帰納定理により記述される自然数
- 数論
- 整数
- 有理数
- 合同式
- 基数
- 順序数
- 数(自然数)とは何か?
第3章:幾何学
- 空間にかかわる諸活動
- 図を使わない証明
- 平行線の公理
- 双曲幾何学
- 楕円幾何学
- 幾何学的量
- 向き付け
- 幾何学における群
- 立体幾何学
- 幾何学は科学であるか?
第4章:実数
- 大きさの測定
- 幾何学的量としての大きさ
- 大きさの操作(演算)
- 大きさの比較
- 実数の公理
- 実数の算術的構成
- ベクトル幾何学
- 解析幾何学
- 三角法
- 複素数
- 立体射影と無限遠点
- 虚数は現実のものか?
- 抽象代数登場
- 四元数その他
- 要約
第5章:関数、変換および群
- 関数のタイプ
- 写像
- 関数とは何か
- 対の集合としての関数
- 変換群
- ガロア理論
- 群の構成
- 単純群
- 要約:像と合成という考え方
第6章:微積分学の諸概念
- 起源
- 積分法
- 微分係数、導関数
- 積分法の基本定理
- ケプラー(Kepler)の法則とニュートンの法則
- 微分方程式
- 微積分学の基礎づけ
- テイラー(Taylor)級数と近似
- 偏導関数、偏微分係数
- 微分形式
- 微積分学から解析学へ
- 諸概念のあいだの内部関連
第7章:線形代数
- 線形性の源泉
- 線形変換と行列
- 固有値
- 双対空間
- 内積空間
- 直交行列
- 随伴変換
- 主軸定理
- 双線形性とテンソル積
- 商空間
- 外積代数と微分形式
- 相似性と直和
- 要約
第8章:空間が有する形式
- 曲率
- 曲面のガウス曲率
- 弧長と内在的幾何学
- 多価関数とリーマン面
- 多様体の例
- 滑らかな多様体
- 径路と量
- リーマン計量
- 層
- 幾何学とは何か?
第9章:力学
- ケプラーの法則
- 運動量、仕事、エネルギー
- ラグランジュの方程式
- 速度と接束
- 数学における力学
- ハミルトンの原理
- ハミルトンの方程式
- トリックとアイデア
- 主関数
- ハミルトン-ヤコビの方程式
- 回転ごま
- 力学の形式
- 量子力学
第10章:複素解析とトポロジー
- 1変数複素関数
- 病的関数
- 複素微分
- 複素積分
- 平面上の径路
- コーシーの定理
- 一様収束
- 冪(べき)級数
- コーシーの積分公式
- 特異点
- リーマン面
- 芽と層
- 解析学、幾何学、位相数学
第11章:集合、論理、圏
- 集合の階層
- 公理的集合論
- 命題計算
- 第1階の言語
- 述語計算
- 正確な推論と理解
- ゲーデルの不完全性定理
- 独立性の証明
- 圏と関手
- 自然変換
- 普遍性
- 写像の公理
- 直観主義の論理
- 層の方法による独立性の証明
- 基礎付けか組織化か?
第12章:数学のネットワーク
- 形式性
- アイデア
- ネットワーク
- 部門、分野および下位区分
- 問題
- 数学を理解するということ
- 一般化と抽象化
- 新機軸
- 数学は真実か?
- プラトニズム
- 好ましい研究の方向
- 要約
参考文献
記号一覧
訳者あとがき
索引




















「二重の発見ですね」という言葉には含蓄があります。
実生活で蓄積した知識から本質を抽出したという意味でユークリッド幾何学の発見はマクレーン教授のおっしゃる意味での「抽象化」であり、非ユークリッド幾何学」は直線を曲線にするという表面的な「一般化」を超えた「発見」なのだと思いました。
hirotaさんにそうおっしゃっていただくと心強いですね。
では「公理」はどうなんだ?という問いを考えたことがありますが、ユークリッド幾何学の公理にしても非ユークリッド幾何学の公理にしても、それぞれ幾何学の世界を矛盾なく発展させ整合性をもちながら数学の中で生きていますから「出発点」を発見したことになるのだと思います。