
![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む26年度の問題を取り上げ、ポイントを解説します。
前回に引き続いて、中学入試問題の図形問題で、経験的に覚えていなければならない問題を取り上げ解説します。学校では小学4年生で学習する、二等辺三角形の性質を使う問題を、今回と次回の二回に分けて説明しましょう。
学校で学習する二等辺三角形の性質を問う入試問題は、頻出問題と言えるほど、今回取り上げた学校以外にも多くの学校で出題されています。
【26年度の入試問題】 (分数の表記および記号が、実際の入試問題と若干異なります。)
今回は、高輪中学校・品川女子学院中等部・横浜雙葉中学校の入試問題を取り上げます。
1.高輪中学校
下の図のように、正三角形ABCの辺BCをのばした直線と、頂点Aを通る直線が、点Eで交わっています。また、AC=CD=DEです。図の(あ)の角の大きさは何度ですか。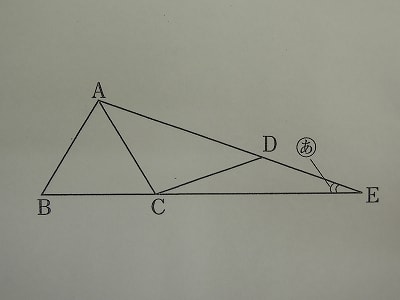
2.品川女子学院中等部
次の図で角アは角イの4倍の大きさで、辺BC,CD,DE,EFの長さは等しいです。三角形AEFが二等辺三角形であるとき、角ウの大きさは□°です。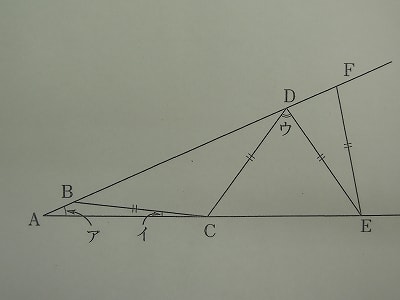
3.横浜雙葉中学校
下の図の三角形ABCはAB=ACの二等辺三角形で、角アは75度、BC=BF=EF,AD=DEです。イの角度は何度ですか。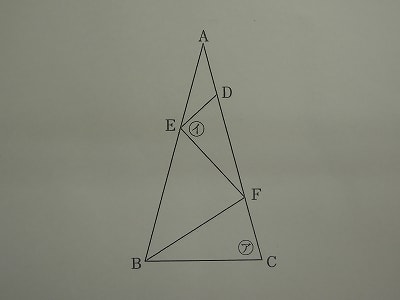
【解答と理解しておくべきポイント】
二等辺三角形の定義は、 「二つの辺の長さが等しい三角形」です。山の形の頂上の角を頂角、下の二つの角を底角と言います。二等辺三角形は、2辺の長さが等しいだけではなく、2つの底角の大きさが等しくなります。
また、頂角の大きさが定まると、残りの底角の大きさが決まり、一つの底角の大きさが定まると、残りの底角および頂角の大きさが決まります。
まず、高輪中学校の問題から解説します。
高輪の算数は、問題1に計算4題、問題2が小問4題、その後それぞれ小問が3つずつある大問が3題出題されました。今回の問題は、問題2の小問の一つです。
この種の問題は、二等辺三角形の底角が等しいという性質と、三角形の外角の定理を上手く使って求める、基本的な問題です。
下の図のように、最も小さな底角Eの大きさを①と置きます。三角形DCEの外角ADCは、角Eと角DCEの和となりますから、その大きさは②です。
同様に三角形ACEの外角BCAは、角Eと角EACの和ですから、その大きさは③と表すことが出来ます。
三角形ABCは正三角形ですので、角BCA=60度=③
よって求める(あ)の角の大きさは、①ですので、60÷3=20度
次は品川女子の問題です。
品川女子の算数の問題は、問題1が計算2題、問題2が小問6題、それに小問が2題ずつある大きな問題が4題で構成されています。今回の問題は、問題2の小問の一つです。
条件の「角アは角イの4倍の大きさ」から、角イをもとにしていますので、角イの大きさを①と置きます。すると角アの大きさは④となります。
高輪中学と同様に、二等辺三角形の性質と、三角形の外角の定理を使って、それぞれの角の大きさを下の図のように表してみます。
三角形AEFが二等辺三角形であるなら、頂角の大きさが④で、底角の大きさが⑬と表すことができます。
よって、④+⑬×2=180という式が出てきます。
マル30=180度ですので ①=6度
よって求める角ウの大きさは、
180-(⑤+⑬)=180-⑱=180-6×18=72度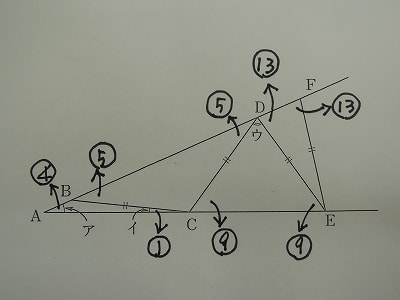
最後は、横浜雙葉の問題です。
横浜雙葉の算数は、問題1が計算を含む小問8題、問題2は小問4題・問題3が小問3題で構成された大問で作られています。
今回問題は、問題1の小問の一つとして出題されています。
条件を図に記入します。まず一番大切なことは、三角形ABCと三角形BCFは底角が共通の75度ですから、相似な二等辺三角形であることに気づくことです。
頂角75度の二等辺三角形の頂角の大きさは、
180-75×2=30度
よって角A=30度ですので、外角の定理より角EDF=30×2=60度
また角EBF=角ABC-角FBC=75-30=45度、
角BFE=180-45×2=90度
このことから、角EFD=180-(75+90)=15度
角イ=180-(角EDF+角EFD)=180-(60+15)=105度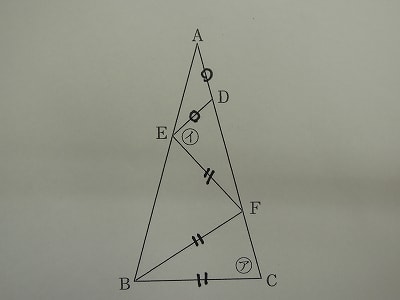
以上の問題とその解法を理解すると、こうした問題に目が慣れて来るはずで、そうした経験が、新たな問題を考えるときに解き方のヒントになります。
次回は、今回と同様に二等辺三角形の性質を使う問題ですが、少し変形された問題について考えてみましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む26年度の問題を取り上げ、ポイントを解説します。
しばらく数量系の問題を中心にピックアップしてきましたが、図形に関する問題にも、経験的知識を必要とする問題がいくつか存在します。そうした問題を中心に、今度は図形関連問題を取り上げ解説していきましょう。
【今春の入試問題】 (分数の表記は、実際の入試問題と異なります。)
慶応中等部の問題は、学校の難易度に比べ解き易い問題が多いので、慶応中等部に合格するためには、点数差が少ない分、その後の面接が重要となると言えるでしょう。慶応中等部を受験した子どもたちの多くは、テスト後、その出来を自己採点して、「先生、合格したよ!」といった反応を示すほど、比較的出来の良い答案を書くことができます。
慶応中等部の26年度の算数は、問1が計算4題、問2が小問4題、問3は図形の小問4題、その後4つの大問4題で構成されています。今日取り上げる図形3題は、問3の小問のうちの3題です。
これらは、入試問題としては、基本的ワンパターン問題と言えますが、今回のテーマ「経験的知識が必要な問題」でもあり、知らないと解くのに苦しい問題です。この出題内容を勘案すると、この問題の出題者は、比較的若手で、中学入試問題を分析してその奥深さを知り始めた数学教師であると、推測できます。
3.(2)
[図1]は、正方形と半円と、中心角が90°のおうぎ形を組み合わせたものです。角Xの大きさは□°です。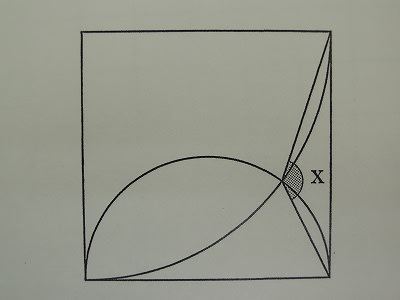
[図1]
3.(3)
周りの長さが26cmで、最も長い辺の長さが12cmの同じ直角三角形8つを、[図2]のように並べました。色のついた部分の面積は□平方cmです。
[図2]
3.(4)
[図3]のように、半径が18cmの半円を、まっすぐな線で2つの部分に分けました。色のついた部分の面積は□.□平方cmです。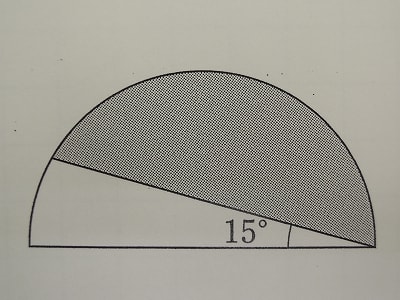
[図3]
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
【解答と理解しておくべきポイント】
この問題は、うまく補助線を引けるかどうかが決め手となります。中学数学でも補助線を引くことにより、解決の糸口とする問題は多いのですが、その線を引けるかどうかは、「図形的センス」と考える教師は多いはずです。しかし、今回のテーマである「経験的に修得すべき基礎的知識」が重要であって、日頃の学習経験が活用できる知識にまで高められているかどうかが問題だと私は考えています。教師は体系的に教えること、生徒は分析的に考えることが重要です。
まず3.(2)の解答です。
父母の皆さんで、私のこの解法を見ずに正解した方は、Very Good! まず、この問題は、点Aから点Eと、点Bから点Eに補助線を引きます。すると三角形ABEと三角形AEDができますが、いずれも2辺が同じ円の半径となっていますので二等辺三角形です。
補助線を引くことによって、気付かなかったものが見えてくる!
2つの二等辺三角形の低角を図のように、それぞれa度とb度とすると、以下のことが分かります。
四角形ABEDの内角の和は360度で、角DABは90度ですので、
a×2+b×2+90=360
(a+b)×2=270
a+b=135
また、直径BCの上の角(円周角)は90度ですので、求めるXの角度は、
360-(135+90)=135(度)
[図4]
次に、3.(3)の解答です。
この問題は、比較的簡単な問題で、解き方に気付く受験生は多かったと思われます。条件から、下のように長さを表すことができます。すると一番大きな正方形から2番目に大きな正方形を引くと、直角二等辺三角形4つ分の面積を出すことができます。
14×14=196
12×12=144
196-144=52
下の図から、2番目に大きな正方形から4つの直角二等辺三角形を引くことにより、求める一番小さな正方形の面積を求めることができます。
144-52=92(平方cm)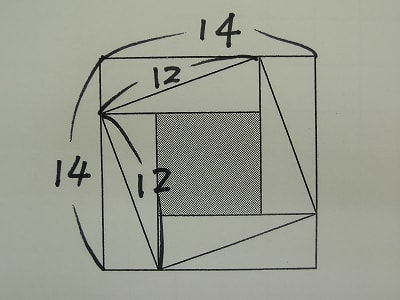
[図5]
最後は、3.(4)の解答です。
この問題を出題すると、半円から中心角15度のおうぎ形を引く生徒をよく見かけます。中心角15度のおうぎ形に見える図形は、よく考えるとそうではないことが分かるはず。同じ長さの半径2つと弧に囲まれた図形がおうぎ形なので、この場合2辺の長さが等しくないことは一目瞭然。
この問題は、色を塗った部分(弓形)を含むおうぎ形から、低角15度の二等辺三角形を引くことにより求めます。問題は低角が15度の二等辺三角形の面積を求めることができるかどうかです。これは、実は基本事項です。
下の図の斜線部分の直角三角形は、角が30度・60度・90度の特別な三角形です。三角定規にもなっていて、中3の三平方、高1・2の三角比・三角関数にも登場する三角形です。
この直角三角形の斜辺と一番長い辺の長さの比は、2:1であることは、小学4年で知っていなければなりません。斜辺はこの円の半径18cmですので、最も短い辺の長さは9cmです。
おうぎ形の面積から引く二等辺三角形の高さは、いま求めた直角三角形の一番短い辺の9cmです。よって求める面積は、
18×18×3.14×150/360-18×9÷2
=423.9-81
=342.9(平方cm)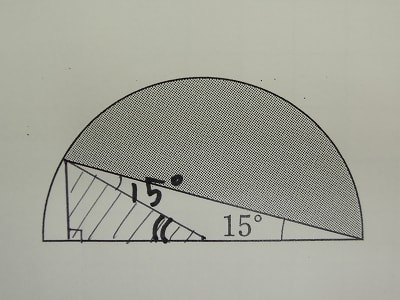
[図6]
次回は入試頻出問題であり、学校でも小学4年で学習する二等辺三角形の性質を使って解く問題について取り上げ分析してみましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む今春の問題を取り上げ、ポイントを解説します。
速さの問題は、公式を使う基本的な文章題の他に、速さに関する特殊算として、旅人算・通過算・時計算・流水算などが、毎年頻繁に出題されます。速さの公式の理解を深め、速さと道のりと時間の関係式から、比例・反比例を使う問題も数多く出題されます。
今日解説する問題は、速さの文章題の主流の問題ではありませんが、おとなも勘違いする問題として、毎年出題されます。ですから、注意する問題の一つとして、理解しておく必要があります。
【今春の入試問題】 (分数の表記は、実際の入試問題と異なります。)
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
1.東京家政学院中学校
家から学校まで、行きは分速50m、帰りは分速70mで往復しました。往復にかかる時間が合わせて18分のとき、家から学校までの距離は□mです。
2.東京女学館中学校
A地点とB地点の間を、行きは時速5kmで、帰りは時速12kmで往復します。このとき行き帰りの平均の速さを求めなさい。ただし、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
3.女子学院
ある姉妹が家から郵便ポストまで同じ道を往復しました。妹は、行きは分速80m、帰りは分速60mで歩き、姉は行きも帰りも分速□mで歩いたら、往復にかかった時間は2人とも同じでした。
【解答と理解しておくべきポイント】
大人であるなら、日頃の経験から、平均の出し方は常識として知っているはずです。その常識が考える目を曇らせ、正解に到達できない問題を今日は取り上げます。
まず初めの東京家政の問題は、今回のテーマである往復の平均の速さの問題ではありません。しかし、行きと帰りの速さを示して、道のりを求める典型的な問題ですので、ちょっと考えてみましょう。
速さと時間と道のり(距離)の3つの数値関係を、受験生はしっかりと理解しておく必要があります。こうした語彙も、3つの関係の公式も覚えずに、漠然と答えが出れば良いではないか、そうした考えの指導者がいますが、それは間違いです。
この問題は、「道のりが一定のとき、速さと時間は反比例する」という基本事項を知っているかどうか試す問題です。
速さの公式、道のり=速さ×時間ですので、道のり一定なら、速さと時間の積が一定ですので、反比例になります。・・・ここがこの問題のポイントです。
速さの比は、条件を整理して行き:帰り=50:70=5:7ですので、かかる時間は、その比の逆比7:5となります。
そこで往復の時間18分を、7:5で比例配分して行きの時間を求めることができます。
18×7/(7+5)=10.5(分)・・・行きにかかった時間
よって求める家から学校までの距離(みちのり)は、50×10.5=525(m)
次は、東京女学館の問題です。
平均=合計(総和)÷個数で求めることは、学校で学習します。そこで、表面的な理解しかしていない受験生は、この公式を使い(5+12)÷2=8.5と解答し、四捨五入せずに答えが出ちゃった!なんてことになります。大人も、一般的な経験から、この式を使って答えを出す人が多いはずです。
この問題は、速さを求めるのに、基本に戻って道のりと時間を計算して出します。ただし、問題の中にAB間の道のりが出ていません。そこで、計算上簡単になるように、道のりを速さの5と12の最小公倍数60と仮に置きます。 「分からなかったら、1と置く」という基本的な考え方で、道のりを1と置く方法もあります。私は、この方法が好きなのですが、分数計算になるのが難点です。
往復の道のり60×2=120、行きにかかった時間は60÷5=12、帰りにかかった時間は60÷12=5
よって求める往復の平均の速さは、道のり÷時間の公式を使い、120÷(12+5)=7.05と求めることができます。
求める答えは、小数第2位を四捨五入し時速7.1kmとなります。
最後は、女子学院の問題です。
「妹は、行きは分速80m、帰りは分速60mで歩き、姉は行きも帰りも分速□mで歩いた」という条件から、姉の速さは妹の往復の平均の速さとなることが分からなければなりません。
そこで、妹の往復の平均の速さを求めます。
前の東京女学館の解き方を使います。速さの80と60の最小公倍数240を道のりと仮定します。基本に戻って、速さ=道のり÷時間で計算します。すなわち、往復の道のりを往復にかかった時間で割ることにより、往復の平均の速さを求めます。
240×2÷(240/80+240÷60)=480÷7=68と4/7
求める姉の速さは、分速68と4/7mとなります。
小中学校で学習する公式は、大変基本的な考えが含まれています。表面的な暗記だけではなく、しっかりとその内容を理解しておくことが大切です。
次回から、図形の問題を取り上げて、注意すべきポイントをお教えしましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む今春の問題を取り上げ、ポイントを解説します。
今日のテーマは、日常においても様々な場面で常識として取り扱われる考え方を含む問題です。特殊算の中でも、最も有名な問題の一つである「植木算」について取り上げます。
長年この問題は、入試問題として出題され続けています。規則性の問題ですが、物事をしっかりと考える習慣のない人は、ミスしがちな問題の一つです。
【今春の入試問題】 (分数の表記は、実際の入試問題と異なります。)
1.開智中学校
100cmのアメを、5cmごとに切り、20個のアメに分ける作業を行います。この作業は、1つ切り分けるために20秒かかり、1つを切り分け終えてから、次を切り分け始めるまでに10秒かかります。すべてを切り分けるためには、□分□秒かかります。
2.大妻中学校
縦3cm、横8cmの長方形の紙を、のりしろを□cmにして、横方向に16枚つなげてできる長方形の面積は321cmです。
3.桜蔭中学校
同じ大きさの小さい正方形の紙をはりあわせて大きい正方形を作ります。小さい正方形の紙の1辺の長さの1/8の長さをのりしろとして、たて、よこ12枚ずつ、全部で144枚の小さい正方形の紙をはりあわせます。大きい正方形の面積は小さい正方形の面積の何倍ですか。
【解答と理解しておくべきポイント】
植木算は、他の学校でも、その考え方を使う問題が多く出題されています。単に木を植えたり、旗を立てたりする問題以外に、様々な問題に顔を出す考え方です。ですから植木算は、自在に使いこなせる基本的知識として、しっかりとマスターする必要があります。それでも毎年出題されるのは、基本を覚えず勘違いする受験生が多いからでしょう。
まず開智中学の問題から解説しましょう。
この問題は丸太を輪切りにする問題で、よく出てきます。単に植木算の考え方を使う問題というよりも、ちょっとした注意力を試す問題として出題されます。
アメを2つに切り分けるとき、1回切ればよいことは分かりますね。アメを20個に分ける場合、切る回数は20-1=19回です。これは、植木算の考え方です。ただし、間の10秒は、最後に切ったときだけ、必要ありません。切り終えて、10秒休憩した後に、切り終えました!と言うことはありません。
こうした問題を出題する教師は、よほど受験生の注意力を試すことに固執していると言えるでしょう。
20×(20-1)+10×(20-2)
=380+180
=560(秒)
560秒=9分20秒・・・答え
次は、大妻の問題です。
小さな長方形をつなげてできた大きな長方形の面積とたての長さは分かっています。この条件から、横の長さを求めます。
321÷3=107(cm)・・・横の長さ
8cmの紙を横にのりしろ無しで16枚つなげた時の横の長さは、8×16=128(cm)です。
16枚の長方形をつなげると、のりしろは16-1=15箇所できます。ここが、植木算の考え方です。
128-107=21(cm)短くなった理由は、のりしろ15箇所の長さの合計です。
よって求めるのりしろの長さは、21÷15=1.4(cm)です。
最後は、桜蔭の問題です。
方針としては、小さい正方形の一辺の長さを1と置きます。大きな正方形の一辺の長さを、植木算を使って出し、その結果から大きい正方形の面積が小さい正方形の面積の何倍になっているかを求める方法をとります。
小さい正方形の1辺の長さ(1とする)の1/8の長さをのりしろとして、12枚つなげた大きな正方形の一辺の長さは、のりしろが12-1=11箇所(植木算)あることを考えて求めます。
1×12-1/8×(12-1)
=12-11/8
=85/8・・・大きな正方形の一辺の長さ
したがって、求める大きな正方形の面積は、
(85/8)×(85/8)
=7225/64
小さい正方形の面積は、1×1=1ですので、求める何倍かという問の答えは、
7225/64=112と57/64倍(実際の分数表記と異なる)となります。
「植木算」は、大きな範疇に含まれる問題ではありませんが、考えの詰めがしっかりとできるか試す問題です。そうした力を見る問題は、他にも幾つかあります。
例えば「2けたの整数で、2でも3でもわれない数は幾つありますか。」といった問題です。この例題は、「1から100までの整数の中で~」の条件に比べて、計算量が3倍となります。それから2けたの数は、10から99まで90個あるのを、89個としてしまうと、いっぱいやった計算の努力が水の泡となってしまいます。
また、日数・曜日計算は、植木算と同様に詰めが甘い受験生にとって、ミスが出る問題の一つです。例えば、「11月25日が火曜日なら、その年の7月7日は何曜日でしたか。」などが代表例です。日数計算で1日ずれる場合があります。また、曜日計算も同様にミスするポイントがあります。自分がやっていることを理解し、細かい点に注意力を働かせることができる受験生は、それらのミスしやすいポイントを、的確に解いて間違えることはありません。
以前に、植木算を含む特殊算についての考察を、以下のブログで綴りました。興味ある方は参考にご覧下さい。
マッキーが教える小学生の算数…算数の『特殊算』について考える

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む今春の問題を取り上げ、ポイントを解説します。
今日の課題は、約数・公約数を求めるとき、ベン図を使って考えたり、具体的に書き並べて考えることができるようにしておくことです。また、最大公約数・最小公倍数を連除法で求める方法を理解し、その中で使われる数値の関係性を知ることです。
【今春の入試問題】 (分数の表記は、実際の入試問題と異なります。)
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
1.本郷中学校
A/42と表される0より大きく1より小さい分数について、これ以上約分されないような分数になるときに、Aに入る整数は何個ありますか。
2.開成中学校
以下の文章のア~ウに当てはまる数を答えなさい。3つの整数ア、イ、ウがあります。アとイの最大公約数は21、イとウの最大公約数は35、アとウの最大公約数は98です。また、アとイとウの合計は1000以下です。
【解答と理解しておくべきポイント】
大学合格実績が大きく伸びた本郷と、御三家開成の問題を取り上げます。
まず本郷の問題です。
前回も解説した分数の約分に関わる問題です。これ以上約分できない分数を既約分数と呼びますが、与えられた条件内の既約分数の個数を求めます。
分子のAは、条件から1以上41以下の整数です。
分母の42を素因数分解すると、42=2×3×7となります。分子Aと約分されない分数の数をもとめるためには、41個の数字から、2と3と7の倍数の数を除けばよいことは直ぐに分かりますね。
ただし、2と3と7の倍数の個数を求めるのは、小学生にとって少々難しい問題となります。集合で、2つの倍数の個数を求めるのは小4のテーマであり、3つの倍数の個数を求める問題は、小5の学習範囲です。3つの数の倍数をベン図で考えると、円が2重に重なった部分と、3重に重なった部分があることが分かります。小学生にとって、ちょっと大変な計算となります。
けれども今回の入試問題は、考慮すべき数の範囲が小さいので、本来の計算で出す方法を採らずに、書き上げて求めた方が遙かに簡単にできることに気づく必要があります。
2と3と7の倍数の数を除いた数を順に書いていきますが、偶数はすべて2の倍数ですからすべて除かれ、チェックする数はかなり限定されます。
よって求める分子を数え上げると、1,5,11,13,17,19,23,25,29,31,37,41の12個となります。
ちなみに計算で出す方法を記しておきましょう。(無論、ベン図を書いて考えます。)
2の倍数…41÷2=20あまり1
3の倍数…41÷3=13あまり2
7の倍数…41÷7=5あまり6
2と3の公倍数(6の倍数)…41÷6=6あまり5
2と7の公倍数(14の倍数)…41÷14=2あまり13
3と7の公倍数(21の倍数)…41÷21=1あまり20
2と3と7の公倍数(42の倍数)…0個
よって2または3または7の倍数の個数は、
20+13+5-6-2-1+0=29(個)
1から41までの整数のうち、2でも3でも7でもわれない数は、
41-29=12(個)
多くの問題は、数え上げるのではなく、計算で出すように指導しますが、今回の問題のように、計算で出すよりも数え上げた方がはるかに簡単な問題もあることを知っておく必要があります。
次は開成の問題です。与えられた最大公約数を素因数分解した形で条件を整理すると、以下のようになります。
ア イ ウ
3×7 3×7
5×7 5×7
2×7×7 2×7×7
アからウまで、それぞれの下に書かれた2つの最大公約数について、次にその2つの数の最小公倍数を下に書いてみましょう。
ア イ ウ
2×3×7×7 3×5×7 2×5×7×7
=294×△ =105×□ =490×○
ア・イ・ウは、それぞれ294・105・490の整数倍であり、△と□と○は「互いに素」の関係の数字が入ります。
ここまで整理すると、この先が難しい問題となりますが、「アとイとウの合計は1000以下」という条件で救われます。
アからウまで書かれた最大公約数の最小公倍数の和は、294+105+490=889となります。したがって、△と□と○はそれぞれ1とせざるを得ず、ア=294、イ=105、ウ=490が答えとなります。
ちょっと待ってください! □を2としても、合計は999となり、条件に合うのでは?
しかし、最終的なアの因数には2が含まれいますから、イの因数の中に仮に2があるとすると、アとイの最大公約数は、与えられた条件の3×7ではなく、2×3×7となってしまい、題意に合いません。
基本をしっかりと押さえておけば、開成の入試問題さえ、正解することができます!
今回で、今春の入試問題における「計算」・「数の性質」の問題を終了して、次回から毎回出題され間違いやすい文章題(小問)や図形の小問について、経験的に覚えておくべき問題を取り上げ説明しましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む今春の問題を取り上げ、ポイントを解説します。
今日の入試問題のポイントは、わり算および分数の約分において、因数に注目した解き方をマスターすることです。整数のわり算を分数に表記すれば、分母の因数がすべて分子に入っていれば、約分されて整数となります。
また単位分数(分子が1の分数)の中で、1/2=0.5のように割りきれる分数と、1/3=0.33333・・・・のように割りきれずに、循環小数(同じ数の繰り返し)となってしまうものがあることを知っている必要があります。
そうした基礎的な数値の知識を問う問題が、今日の一行題です。
【因数とは】
因数という言葉をブログでは、私は使っていますが、小学生の授業中では用いない言葉です。ただし、素因数分解という言葉を使い、さまざまな問題を解いていますので、因数とはどういった言葉かは、子供たちはおおよそ理解しています。因数とは、整数が幾つかの整数の積の形で表されているとき、そのそれぞれの整数をいう言葉です。また,因数はその整数の約数でもあります。例えば12=2×2×3という風に、12を素数の積で表すことができますが、それぞれの数が因数です。
【今春の入試問題】 (分数の表記は、実際の入試問題と異なります。)
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
1.東京都市大学附属中学校
整数を1から81まで順にかけ合わせた数1×2×3×・・・・・・・×81は、15で□回割りきることができます。
2.慶應義塾普通部
1/4を小数で表すと0.25となり、わり切れます。1/3は0.333・・・となり、わり切れません。偶数の積2×4×6×・・・×20をAとするとき、B/Aがわり切れるような最も小さい整数Bを求めなさい。
【解答と理解しておくべきポイント】
入試問題では、特に最初に出てくる一行題的な問題には、受験生に知っていてほしい大切なポイントが必ず1つ含まれています。それが何なのか?・・・それを的確に見つけることが必要です。
まず、東京都市大学附属の問題です。
1×2×3×・・・・・・・×81÷(15×15×15×・・・)
=1×2×3×・・・・・・・×81/15×15×15×・・・
上のように、わり算を分数の計算として考えると分かりやすいですね。そして約分することにより、分母が1となる時の15の最も多い個数を求めます。
15=3×5と素因数分解できます。約分とは、分母分子を同じ数で割ることです。分子の数値を素因数分解すると、3という因数はいっぱい出てきますが、5という因数はさほど多くはないことに気づく必要があります。
要するに、分子=1×2×3×(2×2)×5×(2×3)×7×(2×2×2)×(3×3)×(2×5)・・・・・・、このように10までの積を素因数分解すると、3が4個で5が2個あり、3の方が5の2倍あることが分かります。
そのことから、15の個数は分子の中の5の個数によって決まる!・・・ここを押さえることが必要です。
1×2×3×・・・・・・・×81の中に、5の因数がいくつあるかを考える場合、5の倍数がいくつあるかを調べればよいことは分かりますね。
81÷5=16・・・1(5の倍数は16個)
では、5という因数が16個かと言えば、それは間違い。5×5=25の倍数は、5という因数を2個持っています。5×5×5=125の倍数は、5という因数を3個持っています。
そこで、25の倍数の個数を考えます。
81÷25=3・・・6(25の倍数は3個)
ただし、25の倍数が3個あれば、その中に5の因数は6個あります。しかし、25の倍数は、5の倍数としてすでに1回数えているので、数えていない因数5は3個です。
よって分子の中の5の因数の個数は、16+3=19(個)となり、15で19回割りきることができるというのが正解です。
次に慶應普通部の問題です。
ちょっとこの問題と関連して、分母が偶数の単位分数の中で、分数を小数にしたときに、わり切れるものとわり切れないものを分類してみましょう。
わり切れる・・・・・1/2,1/4,1/8,1/10,1/16,1/20
わり切れない・・・1/6,1/12,1/14,1/18
この分類が即座にできるでしょうか。どうしてわり切れないのかといえば、分母に3または7の因数を含んでいるからです。したがって、求める分子Bが、分母に含まれる3と7の因数の積であれば、分母の中の3と7の因数は約分されて無くなり、わり切れる分数となります。
2から20までの偶数の中で、3と7の因数を含む数は、
6=2×3、12=2×2×3、14=2×7、18=2×3×3です。
よって、求める分子のBは、3が4個と7が1個の因数で構成される数とすればよいことになります。
このことから、B=3×3×3×3×7=567が答えとなります。
数を取り扱うさまざまな問題の学習を行う時に、数の性質をしっかりと理解して行うことが大切です。ただ単に、解答を得るだけではなく、数が持つさまざまな性質に目配りすることは、数を鳥瞰的に見て利用する力を養成することにつながります。
一流のサッカー選手が、自在にボールを操るのと同様に、与えられた数を自由に使えるよう練習するとともに、興味を持って楽しんで学習することが大切です。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む問題を取り上げ、ポイントを解説します。
今日取り上げる問題は、整数の性質や計算をしっかりと学習している受験生にとって、比較的簡単に解ける問題です。けれども、こうした分野の学習を漠然と行っている子どもにとっては、厄介な問題でもあります。出題が減少傾向だった「数の性質」に関わる問題が、近年は多く出題されています。しっかりと学習しておきましょう。
【今春の入試問題】 (分数の表記は、実際の入試問題と異なります。)
このシリーズで取り上げる今春の中学入試問題は、私の解答・解説を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
1.共立女子中学校
1/100,2/100,3/100,・・・・・・99/100,100/100の中で、約分できない分数は何個ありますか。
2.早稲田中学校
次の式を計算したとき、小数第7位の数はいくつですか。
3/16÷(5×5×5×5×5×5×5)
3.青陵中学校
2,4,5を1回ずつ使ってできる3けたのすべての整数の積は、一の位から0が□個続いて並びます。
【解答と理解しておくべきポイント】
上の三つの問題とも、整数の性質および数の規則を理解していれば、比較的簡単に解ける問題です。その規則とは、10を素因数分解すると、2×5と表すことができるということです。
4×15でも良いんじゃないですか。
4×15=(2×2)×(3×5)=2×3×(2×5)=6×10=60
このように、10すなわち後ろに0が付くのは、2×5という因数の積あるからです。
では、今春の共立の問題から考えてみましょう。分数を約分するということは、分母・分子を同じ数で割ることです。それは、分母と分子に共通の因数があるということでもあります。
分母の100を素因数分解すると、100=2×2×5×5となり、分子に2および5の因数がある場合、約分できることを表しています。
1から100までの整数で、2の倍数および5の倍数を除いた個数が、求める個数となります。こうした問題は、集合の問題として取り扱われる基本問題でもあります。
よってベン図を描く(小4で学習)と分かりやすいのですが、2の倍数の個数と5の倍数の個数を加えてしまうと、2と5の公倍数、すなわち10の倍数は2度数えてしまうことになります。例えば、10は2の倍数として1回数え、5の倍数として再び数えてしまうことになります。
よって求める個数は、
1から100までの整数の数-(2の倍数の数+5の倍数の数-10の倍数の数)となります。
2の倍数の数、100÷2=50
5の倍数の数、100÷5=20
10の倍数の数、100÷10=10
よって求める分数の個数は、100-(50+20-10)=40(個)
次は、早稲田中の問題です。問題文に、「次の式を計算したとき~」と書いてあるので、このまま計算するのでしょうか?やはり工夫して解かないと、とんでもないことになりそうです。
与えられた3/16÷(5×5×5×5×5×5×5)の式のわり算の部分は、書き換えれば分母16にかけることになります。
よって、3/16÷(5×5×5×5×5×5×5)=3/16×5×5×5×5×5×5×5
ここで16が2を四個かけた数であることに気づく必要があります。そこで分母を整理すると、
16×5×5×5×5×5×5×5=2×2×2×2×5×5×5×5×5×5×5
=(2×5)×(2×5)×(2×5)×(2×5)×5×5×5
=10×10×10×10×125 (2×5=10はしっかり理解しておく!)
このまま計算しても良いのですが、もう少し工夫する力が必要です。
3/10×10×10×10×125
=3×8/10×10×10×10×125×8 (分母・分子に8をかける)
=24/10×10×10×10×1000 (125×8=1000は基本的数値関係)
=24/10000000
=0.0000024
よって求める小数第7位の数値は、筆算することなく4となります。
最後は、青陵の問題です。
2,4,5を1回ずつ使ってできる3けたのすべての整数の積を考えます。順列の問題ですが、すべての場合の数をもとめる必要はありませんが、今回はすべて求めてみましょう。
小学生は、樹形図を使って小さい順に求めます。
245,254,425,452,524,542の6通りとなります。
この三けたの数値をかけて、0が幾つ並ぶか計算するの?
電卓の持ち込みは、無論できません!
最初の一行題に、そんな時間をかけて良いはずはありません。
この6個の数値をすべて素因数分解して、先ほどから指摘している2×5=10が幾つできるかを考えればよいわけです。ところで、素因数分解すると、2という因数はとても多く出てくることは分かるでしょう。
そこで、2はいっぱいあるのだから、5という因数の数で10が何個できるか分かるということに、気づいたでしょうか。
5の因数が入っている数は、245と425です。
245=5×7×7
425=5×5×17
よって、245×254×425×452×524×542を素因数分解すると、その中に5は3つしか存在しません。
よって、求める0は、一の位から3個続いて並んでいることが分かります。
今日紹介した問題は、いずれも筆算などやっていたら、とんでもない大きな数値になったり、大変な時間を要することになります。入試問題の最初に出てくる一行題に、そんな時間をかける問題を出題するほど嫌みな学校は、そう多くはありません!
日頃の計算練習は、自分が電卓と化して答えを出すだけでは、問題があります。もう少し論理的な考えを取り入れて、数値の相互関係を理解しながら、工夫して問題を解くことが必要です。そうした練習をしている受験生にとっては、今日の問題は、有り難くゲットできる問題と言えるでしょう。
【画像】
一番上が、拾った落ち葉。偶然にできたのか、あるいは誰かの作品か?
二番目は、コスモス。
三番目は、セイタカアワダチソウです。どんな場所にも繁茂し、問題ある帰化植物です。
【セイタカアワダチソウ】
セイタカアワダチソウ(背高泡立草)は、キク科アキノキリンソウ属の多年草である。北アメリカ原産で、日本では切り花用の観賞植物として導入された帰化植物(外来種)であり、ススキなどの在来種と競合する。外来生物法により要注意外来生物に指定されているほか、日本生態学会によって日本の侵略的外来種ワースト100にも選ばれている。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む問題を取り上げ、ポイントを解説します。出来れば、このシリーズで取り上げる今春の中学入試問題は、私の解答・解説を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
前回に引き続き、今年の中学入試に出題された計算問題を取り上げます。整数・分数・小数の加減乗除の計算、□を求める計算、単位が入った計算などが、その入試計算問題の範疇に入ります。
そうした計算の中で、分配・結合・交換の各法則を使うだけではなく、位取りや数値の相互関係を理解して、工夫して解く問題があります。今日の問題は、そうした部類の典型例ですので、理解しておく必要があります。
【今春の入試問題】
1.成城学園中学校
1.2345+12.345+123.45+1234.5=
2.普連土学園中学校
2.014×36+20.14×2.8-201.4×0.17+2014×0.053=
3.筑波大学附属中学校
次の計算をした結果は、何桁の整数となりますか。
4×5×8×25×125=
【解答と理解しておくべきポイント】
まず成城学園の問題は、4つの小数の和の計算です。このまま筆算で計算してもさほど時間はかかりません。小数のたし算の筆算は、位を揃えて計算することを試す問題と考えられます。出題意図が少し曖昧ですが、この問題を工夫して計算する方法を今回は教えましょう。まずこの式を見て、小数点を省けば全て12345の順に数値が並んでいることに気づく必要があります。
そこで、1.2345を基準として1と置くと、12.345は1.2345の10倍、123.45は1.2345の100倍、1234.5は1.2345の1000倍となっていることが分かります。
これを利用して、
1.2345+12.345+123.45+1234.5
=1.2345×1+1.2345×10+1.2345×100+1.2345×1000
=1.2345×(1+10+100+1000)(分配の法則を使う)
=1.2345×1111
=1371.5295
この計算は、そのままやってもさほどの計算量ではないのですが、この方法も気づく必要があります。
次は、普連土学園中学校の問題ですが、「小数計算が、飯より大好きなので、やらせてください!」という生徒は除いて、工夫して解くべき問題です。入試では、筆算を楽しんでいるうちに、刻々と貴重な時間が過ぎて行くことを理解すべきでしょう。疑うようであれば、筆算でやって、時間をチェックしてみてください。入試問題の計算は、難しい問題でも、およそ1分から1.5分程度で解答する必要があります。
この問題は、上で解説した成城学園の計算方法を利用して解きます。
2.014×36+20.14×2.8-201.4×0.17+2014×0.053
=2.014×36+2.014×10×2.8-2.014×100×0.17+2.014×1000×0.053
=2.014×36+2.014×28-2.014×17+2.014×53
=2.014×(36+28-17+53)
=2.014×100(筆算をせずに計算できました)
=201.4
1番の成城学園の問題を、計算の工夫で解こうとする意欲があり、日頃の練習で答えが合えば良いとせず、途中式をしっかりと書くようなことが、計算力を高めるためには大切です。
最後は、筑波大学附属の問題です。筑附のレベルは、長期低落傾向に歯止めがかかっていません。私立に比較して、指導者の力量や情熱に問題があると考えられます。また、最も多くの生徒が塾や予備校通いのダブルスクールで学習しなければならない代表校という、有り難くない評価も気になります。
筑附の入試問題をご覧になれば、与えられた時間に比べ問題量が多いのに驚かされることでしょう。入試問題で、どういった力を見たいのか、疑問符が付く出題となっています。今回紹介する計算は、最初の小問で、1分以内で解くことが要求されています。
日頃の計算練習で、25×4=100、125×8=1000、1/4=0.25、1/8=0.125といった、基本的な数値の関係をしっかりと練習している生徒にとって、とても簡単な問題です。この問題の出題意図を理解できずに、筆算で答えを出そうとしているのであれば、間違いなく合格は遠退きます。
4×5×8×25×125
=(4×25)×(8×125)×5(交換の法則と結合の法則を使う)
=100×1000×5
=500000
よって答えは6桁の整数となります。実際そのまま計算して、「答えは合ったよ!」などと言っていては、力は付きません。
中学入試の計算は、単に答えが合えば良いというものではなく、そのスピートが要求されます。情報処理能力とも言えるそうした力は、日頃の練習の量と質によって培われるものです。しっかりとノットに途中式を書いて練習しましょう。
計算力を身につけるポイントを以前のブログで紹介しました。興味ある方はご覧ください。
マッキーが教える算数…計算力を高めるためのポイント・その1:学習の仕方

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。入試問題算数の初めに出題される計算・一行題は、その学校に合格するために、ぜひ正解してほしい問題です。そうした問題の中で、特に経験的に修得すべき基礎的知識を含む問題を取り上げ、ポイントを解説します。保護者の皆さんや、受験を考えている小学校高学年の子どもが、興味を持てるように綴ります。
私は毎年、その年に出題された入試問題のほとんどに必ず目を通します。毎年出題されるスタンダードな問題・条件を複雑にした凝った問題・難問奇問に該当する問題・新傾向の問題など、様々な問題が各学校の入学試験に出題されます。
図形では、回転移動・転がり移動・対称移動など、大きな枠組みで理解していなければならない問題があります。一方、経験的に覚えておかないと、解法の糸口が見つけられない問題もあります。
今回取り上げる問題は、今年の春に出題された問題の中で、ちょっと頭に入れておいて、ぜひ正解してほしいものを取り上げます。
中学入試問題の算数で、合否を決める問題があるとすれば、それは『出来て当然の問題』と断言できます。各学校で問題レベルは異なりますが、合格するためには、そうした問題を落とさないことが大切です。そうした問題を間違える受験生は、重要事項を覚えていなかったり、ケアレスミスをしてしまうなど、日ごろの学習の質が問題になります。
前口上はそのくらいにして、今日の問題に入ります。取り上げる問題は、分数数列の和の問題です。この計算は、高校で本格的に学習する内容です。けれども、数値の規則性を理解すれば、計算の工夫の面白さがあります。この計算は、大変な手間を掛けて通分しても計算できます。しかし、それでは貴重な時間をロスしてしまいます。計算問題ですが、唯一その計算方法を覚えておく必要がある問題です。
【今春の入試問題】 (注:以下の数式は、実際の入試問題の分数表記とは異なります。)
1.成城学園中学校
1/5×6+1/6×7+1/7×8+1/8×9=
2.立教女学院中学校
1/12+1/20+19/24+1/30+1/42+1/56=
3.早稲田大学高等学院中学部
1/3+1/15+1/35+1/63+1/99=
出来れば、このシリーズで取り上げる入試問題は、以下で示した解答・解説を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
【解答と理解しておくべきポイント】
1番の成城学園の問題が、この計算方法を示しています。分子が1で、分母が連続する2つの整数の積となっていて、それぞれの分数の分母の数を見ると、連続しているといったことが特徴です。このように、解き方のヒントを示した出題形式の学校も多く見られます。
ところで、1/30=1/5×6=1/5-1/6 となることは理解できるでしょうか。
通分を考えると、1/5-1/6=(6-5)/5×6=1/5×6=1/30 となりますが、この逆を利用したわけです。
するとこの式は、以下のように書き換えることが出来ます。
1/5×6+1/6×7+1/7×8+1/8×9
=(1/5-1/6)+(1/6-1/7)+(1/7-1/8)+(1/8-1/9)
上の式から、最初の1/5と最後の-1/9を除いた分数は、 -1/6+1/6-1/7+1/7-1/8+1/8=0 と計算され0となってしまいます。よって、上の式を続けると、
=1/5-1/9
=4/45
この式をそのまま通分すると、分母は2520となり、大変な計算をすることになります。
2番目の立教女学院の問題は、上の解き方を利用しますが、余計な分数(下の青色の分数)が一つありますので、交換の法則で最後にまわします。
1/12+1/20+1/30+1/42+1/56+19/24
=1/3×4+1/4×5+1/5×6+1/6×7+1/7×8+19/24
=(1/3-1/4)+(1/4-1/5)+(1/5-1/6)+(1/6-1/7)+(1/7-1/8)+19/24
やはり、-1/4+1/4-1/5+1/5-1/6+1/6-1/7+1/7 の部分は0となりますから、
=1/3-1/8+19/24
=5/24+19/24
=1
では、3番目の早大学院の問題はどうでしょう。
それぞれの分数の分母を2数の積の形に表すと、1×3、3×5、5×7、7×9、9×11 となり、連続する2つの整数の積とはなりません。
また、今までと同様に考えると、1/3=1/1×3=1/1-1/3=2/3 となって、等式が成り立ちません。
そこで1/3=1/1×3=(1/1-1/3)÷2(または×1/2)と置いてみたらどうでしょう。
1/3+1/15+1/35+1/63+1/99
=(1/1-1/3+1/3-1/5+1/5-1/7+1/7-1/9+1/9-1/11)×1/2
=(1-1/11)×1/2
=10/11×1/2
=5/11
以上のように、この式の書き換えを使うと、ほぼ筆算を必要とせずに、素早く答えを出すことができる問題です。計算問題集には、必ず載っている問題ですので、まじめに計算練習をしているかどうか試す問題と言ってよいでしょう。
今回取り上げた問題は、以前にも紹介していますので、興味のある方は以下のブログをご覧ください。
マッキーが教える入試問題・算数…分数の数列の和をどう解くか
今回取り上げた計算問題は、連除法で分母の最小公倍数を求め、一般的な分数計算のように通分する方法で行うと、大変な計算となります。当然に時間がかかり過ぎ、計算ミスも多くなります。
問題中の数値の規則性を利用して解く、この方法を覚えておくと良いでしょう。今回が、このテーマの初回でしたが、引き続き今春の入試問題から、経験的に理解しておくべき典型的な問題をピックアップして、皆さんに紹介しましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
ネット上で感情的でクレーマー的な主張を撒き散らす者達が使用する共通語彙の一つとして、「絶対」という言葉があります。「絶対許されない。」「~は絶対ありえねー。」など、絶対という言葉が極めて安易に使われます。
非論理的かつ感情的な主張の対極にあり、厳然と存在する「絶対」という語彙を多用することにより、反論に対する防御姿勢をとっているとも言えます。非論理的で感情が先行する主張は、他の考えを熟慮できる余裕は無く、故に非妥協的で、果ては相手を誹謗中傷することも厭わない結果となっているようです。
教育関連の話題さえも同様です。例えば、「5箱あって、それぞれに10個のクッキーが入っている。クッキーの総数は?」という設問を例に挙げ、「私は5が10個分と自然に思い浮かぶ。」という考えを述べて、自分の考えを主張している者がいます。答えを出すだけなら、5×10で50だなと大人が考えることは勝手です。しかし、自分が思いついた5箱×10個=50個という支離滅裂な式を、これから考える力を身につけようとする小学校低学年に対する学習指導にも使うべきだという安直な考えは、大きな間違いです。
この人物は、「答えが合えば式のたて方はどうでもよい」と主張していますが、学校や塾のプロ教師が、常に研究し試行錯誤している教科指導の努力を、いとも単簡に否定しています。自分の考えを式に書き表すことが、子どもが論理的に考える力を深め、算数の学習目的でもあることを、理解していない主張と言えるでしょう。常に匿名で自分の主張を述べているので、どういった人物か不明ですが、言動に責任を持つ意識は希薄なようです。少なくとも、子どもに対する学習指導経験が無いことは、確かです。
進学塾では稀ですが、公立小中学校の指導経験を踏まえて、私は次のような例を挙げて、論理的に式を立てることができない子どもの問題点を、指摘することがあります。「100円のお菓子を2つ買った時の代金は?」という問に対して、100+2=102円という答えや、時には100÷2=50円という答えが返ってくることがあります。
本当ですか? それは本当です! このように、与えられた数値を、しっかりと理解しないまま反射的に答えを出そうとする解き方を、「100円のお菓子2個で102円方式」と私は呼んでいます。このように日常扱うレベルの計算さえも、物事を論理的に考えることをしない子どもは、ミスをしてしまいます。公立小中学校の教師であれば、「102円方式」の解き方を、実感を持って納得できるでしょう。日常的に取り扱う数値感覚が身についていない子どもに対しては、情景図や模式図等を使い、手順を追って指導する教師の努力と忍耐が必要です。
さて、以上のような問題点をクリアし、子どもの算数学習を、効果的に指導するためのテクニックを簡単に教えましょう。まずは、問題の条件を整理することを指導します。これは、なにも入試問題解法だけではなく、上記の問題レベルさえも場合によっては必要です。
100円と書かれたお菓子を2つ、実際に情景図としてノートに書きます。その図を見ながら、どうしたら代金を出すことができるか、考えさせます。下手な指導者は、直ぐに式を書かせて、100+2=102円ですか?……違うんじゃないの! では100-2=98円ですか?……違うね! じゃあ100÷2=50円ですか?………このような指導法は、答えが合えばそれで良しとする、最初に指摘した者と同様の指導法といえるでしょう。
「102円方式」の子どもには、情景図を参考に、「100円のお菓子をまず1つ買うと100円。その後でもうひとつ買えば、また100円。だから、100+100=200円となり、100円が2つ分だから、100×2=200円という式を書いて求めることができるよ。」……こんな風に指導する必要があります。
また、条件を整理すること無く、「~ですか。じゃあ~ですか。それとも~ですか……」方式で答えを「当てよう」としている子どもに対して、注意を喚起するために「102円方式」を持ち出すことがあります。
問題のレベルが上がると、どういったジャンルの問題で、どのように条件を整理する問題かを、まず考えさせます。全ての解法は、既に経験したものから類推して導き出すので、全く発想が湧かない場合、その問題を離れて、知識として持つべき基本からやり直すべきです。
条件を整理→→各種図を書く→→この後に、その考えを式に定着させます。式をいい加減に書いて、答えが合っているかどうかだけが気になる子どもがいます。多くの問題を解いても、学力がアップしない子どもの、これは共通したスタンスです。
問題を解く行為は、答えを出すことが目的ではなく、そうした問題の解き方を経験し、活用できる知識を修得することが大切だと考えてください。自分が書いた式を説明させることは、考え方を反復することで知識を定着させる良い方法です。
簡単にヒントを与えないこと。解くきっかけを、子ども自らが考える、また解く気力を身につけさせることが大切です。もっと言えば、教える者が、子どもの考えることの障害とならないことが必要です。「え~と、1kmは、何メートルだっけ?」・「1kmは、1000mでしょ!」、「えーと、円の面積を求める公式は…?」・「半径×半径×円周率でしょ!」……。
これでは、算数の学習指導になりません。手取り足取り教えて、「先生(お父さんorお母さん)の教え方、よく分かる~!」などと子どもに言われていい気になっていると、実は全然成果が上がっていない指導だったということは、稀ではありません。
算数の指導は、子どもが論理的に、かつ持続的に考えることを、どれだけ支援できたのか、そこが最も大切です。
上の画像は、この時期に咲いているヒマワリ・トケイソウ・ワルナスビの花です。

![]()
ブログ人気投票にクリックいただけると幸いです!
いよいよ都内中学入試が今朝からスタートしました。本人も父母も緊張した朝を迎えたことでしょう。今までの努力を自信に、力いっぱい頑張ってください。今朝は、公立中学校に出向き、中3受験生の数学指導を2コマ行いました。都立推薦入試の結果発表があり、都立志望の公立中学の生徒たちも、受験に突入した感があります。夕刻から、今日の入試の結果が、ネットを活用して次々と発表されました。今日の教室の中学入試結果は、大変良い出来でした。明日も期待したいと思います。
さて、大変忙しい日々の今日この頃ですが、私のこのブログに「あるコメント」を頂きました。この件に関し、私の考えを述べることにうんざりするほど、もうすでに私の考えを明確にこのブログを使い述べています。興味ある方は、一番下に載せますので御覧ください。今回コメントをされた方は、「子どもを持つ親の立場の者」ということでしたので、このコメントに再び応えたいと思います。
【いただいたコメントの内容】
はじめて書き込みさせていただきます。
子どもを持つ親の立場の者です。
かけ算の順序についてです。
http://blog.goo.ne.jp/hps_tokyo/e/da0ebdcf67d59feaf04391460b1b4f4a
の記事を読ませていただきましたところ、マッキー様は
>「かけ算の順序に拘る教え方をする人、及びそれを擁護する人」という
>対象を示す言い回しは正確ではなく、「考え方を式にしっかりと表すこ
>とを指導する教師」と「答えが出せれば式の表記はどうでも良いと考え
>る教師」との対比で表すべきで、「かけ算の順序」という焦点をぼかし
>た言い回しは避けなければなりません。
と仰っておられますので、
「考え方を式にしっかりと表す → 正しい順序の式を書く」
というお考えなのだと理解しました。
さて、ここで質問がございます。
【質問】
2008年10月06日の記事の中で、
「1.5㎞ を m に直す」という換算を
1.5×1000=1500
としておられます。
ここを、児童が
1000×1.5=1500
と書いたら、そちらの教室では バツ 又は
「考え方を式にしっかりと表わせていない」
と判断されるのでしょうか?
よろしくお願いします。
【コメントに応える】
取り上げているのは、1.5km=( )mという単位変換の問題です。
この単位変換を行う場合、まず1kmが何mかを知らなければなりません。1km=100mと答える児童は、例外的な子どもではありません。「では、運動会で《100m競走》と言う代わりに、《1km競走》と言い換えても言い訳ですね。」そう問われて、ちょっとおかしいなと気付くようなことは、公立小学校では稀なことではありません。7年間複数の公立小学校で指導した経験から、お話ししています。
メートル法は、基本的に3ケタで単位が変わります。1km=1000m、1m=1000mmといった具合です。ですから、km単位の数値を、m単位の数値に変換する場合、1000倍すれば良いことが理解できるでしょう。
ですから、1.5(km)という数値を1000倍して、1500mとする考え方が無難です。式であらわせば、1.5×1000=1500(m)となります。
もう一つの考え方は、1000m=1kmを基準にします。1.5kmは1kmの1.5倍と考えます。すると、1kmと等しい数値の1000mの1.5倍が、1.5kmと均しいことが分かります。そこで、1000(m)×1.5(倍)=1500(m)と変換しても、自分の考え方が説明できるなら、問題なく正解です。
ただし説明を付け加えるなら、1.5kmをmに単位変換する場合は1000倍して1500mと答えを出し、1500mをkmに単位変換する場合は1000で割ってやって1.5kmと答えを出す教え方の方が、理解しやすさからすれば優れた教え方です。
実際に公立学校で教えていると、「150mは何kmですか。」または「0.15kmは何mですか。」という問に対して、1000倍するのか、1000で割るのか、そのことさえなかなか理解していない子どもが多いのです。
kmをmのように、小さな単位にすると、数値は大きくなります。逆にmをkmのように、大きな単位に変換すると、数値は小さくなります。この大原則さえも、分かっていないのです。そこで、こうした生徒に対しては、「君の身長は?」と聞きます。すると児童は、「150cmです。」と応えます。では、君の身長は何mですかという問をすかさずします。「1.5mです。」
自分の身長は、cm単位で言えば150cmですし、mの単位にすれば1.5mとなります。このような身の回りの例を示して、上で示した単位変換の原則(小さな単位にすると数値は大きくなり、逆に大きな単位に変換すると数値は小さくなる)を教えなければならないのが現状であることを、ご覧の方はご理解いただけるでしょうか。そのことを前提で、私の話をお聞きください。
もう一つ例を挙げると、1ha=10000平方mですが、この変換を子どもに丸暗記させてはいけません。1平方kmは一辺がkmの正方形の面積、1haは一辺が100mの正方形の面積、1aは一辺が10mの正方形の面積、1平方mは一辺が1mの正方形の面積、1平方cmは一辺が1cmの正方形の面積です。すなわち、1haと1aの正方形の一辺を覚えていれば、面積の単位変換が可能であることが分かるでしょう。
私は、単位変換に関しても、その考え方を子どもに言わせて、日頃練習させます。「1haは、(一辺が100mの正方形だから)100×100で、10000平方mです。」……といった風に答えさせます。ですから、自然と「1ha=10000平方m」という式がまず浮かぶはずです。決して「10000平方m=1ha」ではないのです。
この流れから、「1.5haは何平方mですか。」という問に対しては、
1.5×10000=15000平方mが、考え方の流れからすれば自然です。
また、「15000平方mは何haですか。」という問には、
15000÷10000=1.5haと答えを出します。
子どもは、10000倍するのか10000で割るのかに神経を集中できるのです。
かつて、「5箱があって、それぞれに10個のクッキーが入っている。クッキーの総数は?」という問をある方が設定して、「私は5が10個分と自然に思い浮かびます」とおっしゃっていいました。
簡単に言えば、「あなたがこの設問で浮かんがことを、私は聞いているのではない。算数の道具箱の教材を手を使って用いながら、考える力を身に付けようとする小学校低学年の子どもたちに、如何に分かり易く教えるか。そしてどう教えたら考えを深めることができるのか。そこだけが重要なのだ。」……私は、そういう方に対して、このように言いたいのです。常に教えている時に、センサーを最大限活用して、子どもたちの反応を読み取っている教師なら、このように曖昧な考え方でこの問題を捉えることは決してありません。
単位の入った式は、小学生にとって、考え方を整理するのに役立ちますが、5箱×10倍=50個では意味不明です。10個×5箱分(倍)=50個が自然な考え方で、自分で書いた式を他の人に説明できなければ、考えは深まりません。
中学1年では、円周を求める公式を、S=2πr(2パイアール)と教えます。だからといって、小学生に、2を3.14倍してそこに半径をかけると円周が出ますとは教えません。文字式は、途中の考え方を無視して、文字式の決まり、数値・円周率・アルファベットの順に表記します。それをそのまま、上記のようには子どもに決して教えないのです。
それどころか、習熟度の低い中1に対して、小学生の指導に戻って、半径を2倍して直径を出し、その直径を円周率倍して円周を求めることを教えて式を書かせ、その後文字式のルールで表記し直させるといった指導も多いと思われます。
以前私が批判したネット評論家や、好んでこのような話題をネットで論戦している人たちの多くが、実際の児童・生徒を指導した経験を持っていないことが多いようです。現場の真面目な教師の努力を無にするようなクレーマー的な批判が多すぎるように私には思われます。
今回コメントを頂いた「子どもを持つ親の立場の者」に申し上げたいことは、お子さんの算数・数学のノートには、考え方の道筋をしっかりと書くことをアドバイスしてあげてください。日頃の学習は、答えを出すことが目的ではなく、論理的に考えていく訓練であり、それは他の人に自分が書いた式を基に考えを説明できるような学習であることに留意してください。
以下の内容は、今回のブログに関連して、かつて綴った文章です。興味ある方は、ご覧下さい。
マッキーの教育論:ネット評論家の無責任な教育論
マッキーの算数指導法:式のたて方のコメントに応える
マッキーの算数指導法:式のたて方のコメントに応える(2)
マッキーの算数指導法:式のたて方のコメントに応える(3)

![]()
ブログ人気投票にクリックいただけると幸いです!
今回のブログは、前回の問題の解説です。
《問題》
「パン屋さんで250円のパンを買います。3人でお金を払うのですが、250円は3人で割れないため1人100円ずつ出しておつりをもらいました。そして、50円のおつりをまた3人で分けますが、うまく割り切れないので1人10円ずつもらい、残り20円はユニセフに募金します。
さてここで、逆算してみます。まず100円払っておつりの10円が戻ってきたので1人90円ずつ出したことになります。90円×3人で270円、そこに募金した20円をたすと290円。300円出したのに290円。10円はどこに行ったでしょう?」
《解説》
この問題の設定と同じような考え方のミスを犯す子どもは、教えていると結構います。
この問題を生徒に出した教師は、そんな生徒の解法を見て思いついたか、または、ほろ酔い気分で問題を考えているときに、自らが迷宮に入り込んで思いついた問題か、そんなところでしょう。
現金の出入りを整理すると、まず3人から100円ずつ徴収して、計300円。
次に250円のパンを購入して、50円のおつりをもらい、3人に10円ずつ返します。
この段階で、3人はそれぞれ90円ずつ計270円の出費となります。
この出費270円とユニセフへの寄付の20円を加えると、確かに290円となってしまいます。
ただし270円の内訳は、パン250円とユニセフへの寄付20円がすでに含まれています。
この問題のポイントは、250円のパン+10円×3人分返却+20円の寄付=計300円というお金の流れと、300円出して30円戻ってきて、すでに出したお金から20円を寄付したという、実際に使ったお金の表面的な出来事を混同してしまったところです。
3人が使った270円には、すでに20円の寄付が含まれていて、使ったお金270円+返却したお金30円=300円という本来のお金の流れを見失った結果、このような錯角をしてしまったと考えられます。
こうした考え方の間違いは、簡単に例えれば、きかんしゃトーマスが目的地に向かって走っている間に、ポイントの切り替えを間違えて、気付かぬうちに全く違った方向へ走ってしまっているようなものです。
いつまで経っても目的地に到着せずに、いったいどこのポイントで間違えたのかわからない状態なので、まずは間違えたポイントを探り、そこまで戻って針路を修正する必要があります。
算数・数学の複雑な問題を生徒に解かせると、そうしたポイント切り替えミスの発生をよく見かけます。
単に頭のなかで考えているのではなく、条件を紙面上に整理して、できるだけ論理的な考え方をするように訓練することで、そうしたミスを未然に防ぐことができます。
考えが常に表面で横滑りしてしまう生徒を見かけますが、そうした訓練を意識的に行うことが大切です。

ブログ人気投票にクリックいただけると幸いです!
前回綴った通り、「式のたて方のコメントに応える」その2にひき続いて、今回は「その3」をブログに載せます。
また、前回と同様に、積分定数さん自身のコメントと、積分定数さんに寄せられたコメントの後に、私の考えを青字で記すという形式でまとめましたのでご覧下さい。
(積分定数さんの考え)
順序に批判的な小学校教師のコメントです。
苦手な子も試行錯誤して割合の問題を解いたそうです。苦手な子の解放は教師も気づかなかった方法。
(コメント1)
私自身もそういわれたような気がするし、これまでさして気にもしなかったし、「相手に分かるように式を書く」と主旨も理解していましたが、そういう「子供自身が答えを見つけるためにどうすればいいのか」とは別の、「外部に対して、自分がどう考えていたかを明示するためのあれやこれやのルール」が、子供が自由に考えることの足かせになっているような気がするのです。
前にも書いたけど、出来る子は、自分なりの方法で、合理的な方法で答えを見つけつつ、解答欄の「しき」には、それとは別の、「正しいとされる式」をそつなく書く、なんて芸当はさして苦労もなく出来るかもしれないけど、苦手な子には厳しいと思います。
自分は「正しいとされる式」を子どもに求めることは、ありません。式からすべてを読み取れるわけではないけど、子どもたちがどういう考え方で正解にたどりつくかを楽しみにしています。
<昨年度末、「かけ順考」とともに校内に配布した文書より…>
『おまけのおまけ…「解決の道筋は一つではありません」の実例』
6年生ワークテスト「6年のまとめ」の問題より
問題・「ゆうたさんの組では、家で動物を飼っている人が21人います。これは、組全体の人数の60%にあたります。ゆうたさんの組の人数は何人ですか?」
正解は「くらべられる部分の量÷割合=もとにする量」の公式をもとにした21÷0.6=35 答え35人ですが、これ以外にも…
①21÷60=0.35 0.35×100=35 ⇒1%当たりの人数をもとにした「単位量当たりの考え方」
②21÷6=3.5 3.5×10=35 ⇒10%当たりの人数をもとにその10倍にした「帰一法」
③21÷3=7 7×5=35 ⇒20%当たりの人数をもとにその5倍にした「帰一法」
④60:21=100:x 21×100/60=35 ⇒「等しい比(異種の比)」を使った方法
⑤60:100=21:x 100×21/60=35 ⇒「等しい比(部分同種の比)」を使った方法
⑥21÷3×2=14 21+14=35 ⇒「21人が60%」から、飼っていない40%の人数を求めて足した方法
の6通りの解答がありました。(①~④はそれぞれ複数名いました。)もちろん全て正解としました。算数(文章題)がものすごく苦手な児童で、何とか正解(35人)にたどり着いた児童も多く、「みんなが割合を使って答えを出す⇒割合がわからなければあきらめる」よりも、ずっと嬉しかったです。6年生の伸びを、確かに感じた瞬間でした。
子どもたちは「公式的な模範解答的な式を書く」というよりも、上位の子は「人とは違ういろいろな考え方で正解にたどり着くことを楽しみにしている」下位の子は、「どんな形でもいいから今までの経験を総動員して何とか正解にたどりつきたい」という感覚であったように思います。
個人的な感覚では、子どもが一生懸命考えた子どもなりの考え方を「その単元のが学習で習った公式と違う」という理由で一律に切り捨てて×にするのなら、小学校教員としての資質に欠けているとさえ思います。
この問題は、小学5年の「割合の考え方」と割合の表記法の「百分率」を使って解く問題で、「くらべられる量」とその「割合」から「もとにする量」を求める問題です。
小学年6年で学習する「比」を習った後では、もう少し広い視野で解くことができます。
ワークテスト「6年のまとめ」のタイトルから、小学6年の終わりに算数の学力をチェックするために行ったテストと思われます。
上の文面を拝見すると、子どもたちがきちんと順序よく式をたてた結果、この問題を一般的な割合を使わずに、様々な方法で問題を解いていることが分かり、子どもたちの頑張りに対して拍手を送りたいと思います。
ただし、苦労して頑張ったのは子どもたちであり、本来小学5年で「割合の考え方」を子どもたちに頑張ってマスターさせるべきこの教師の指導成果には、反省すべき問題点があります。
割合の概念を生徒に教えることは、小学校では最も難しい項目の一つであり、教える教師の力量が問われるテーマです。
この項目の習熟度が弱い原因を、「下位の子」と形容して子どもたちに求めるのではなく、教え手の教務能力にあることに、この教師は思いを致すべきです。
子どもたちがあきらめずに頑張ってこの問題に取り組んだことと、教師が割合の概念を子どもたちに教えきれていないという事実を、この教師は混同しているようです。
後日、この教師から割合を現場で教えることの困難についてコメントがありました。割合について子どもたちに習熟させることができずにいることは確かです。私のようなプロの判断からすれば、この教師の誘導が無ければ、考えられまいような子どもの解き方を例に挙げています。極めて不自然な文面を綴ったこの教師の言い分について、あえて今回は目をつぶり是認して、私も以下の指摘をしたいと思います。
ところで、子どもたちが考えたという6つの解き方について、少し触れておきたいと思います。
1と2は、基本的な解き方と言ってよく、1%または10%=1割にあたる数値を出して、その数値を使って100%=1にあたる「もとにする量」を求めています。
割合の問題を線分図等で表記すると、子どもたちはこうした解き方に気づきますが、割合の習熟度が比較的低い場合の解き方です。
3の解き方を使った子どもたちは相当なテクニシャンで、与えられた百分率の数値を、60%の1/3が20%、その20%の5倍が100%となることを見ぬいて、答えを出したことになります。
また、6の解き方は、小学生にとってはノーベル賞ものの解き方であり、21人が60%という条件から、3の解き方と同様に20%にあたる数を求め、それを2倍して40%にあたる値を求め、出てきたその数値と21人を最後に合計することにより答えを求めています。
3や6の解き方で、しかも複数の子どもたちがこの方法を使い問題を解いたと述べていますが、私の長年の指導経験からしても、教師による誘導の結果でなく、子どもたち自らがこの方法を考えだしたとすると、「学力が下位」というこの教師の形容は正しくなく、ほんとうに「小学6年生としてはトップレベルの算数の力を持っている生徒たち」だと断定出来ます。
また、4と5の解き方は、小学6年で学習する「比例式」を使い、おまけにその比例式の解き方を「外項の積と内項の積が等しい」という考え方で子どもたちは解いていますが、この解き方は公立小学校では指導していない「中学3年生レベルの解き方」であることを指摘しておきます。
もしも、こうした解き方が、教師の誘導無く出来たとするなら、この教師が「下位の子」と呼んでいる子どもたちが、小5で学習すべき割合の考え方も習熟せずに、教科書の内容を超えた中3レベルの解き方を考えついたことは、前代未聞の話です。
ただし、こうした考え方よりも基本的な「21÷0.6=35」という式を、小5で割合を教え、かつ小6で比を教えた後になっても子どもたちが思いつかないのは、極めて不自然な現象と言えます。
いずれにしろこの教師が、「算数(文章題)がものすごく苦手な児童」と呼んでいる子どもたちが、ものすごく頑張ってこうした解き方を導き出せたのなら、この教師もこの子どもたちに「割合の概念」を指導することを「下位の子」と決めつけて諦めるべきではありません。
この教師が言うところの「その単元で学習すべき公式」を軽視し未習熟のままに放置するのではなく、この子どもたちと同様に頑張りぬいて、子どもたちに習得させる指導を行うのが、教師の役割であり責務だと私は考えます。
繰り返しますが、この教師が子どもたちに習熟させるべき重要事項を教え切れない事実と、その結果子どもたちが試行錯誤して問題を解いたという話を、論理的にすり替えてはなりません。
公立の中学校で指導していると、割合や速さの考え方を小学校時代にマスターしていない生徒が、その後の数学の学習でとても苦労している事実を、この教師は認識しなければなりません。割合の学習は、答えが出せればよいといったものではなく、割合の概念をしっかりと子どもたちに定着させることが重要なのです。
(コメント2)
>「テントウムシが7匹います。テントウムシには足が6本あります。全部で足は何本あるでしょう
テントウムシには,右前足,右中足,右後ろ足,左前足,左中足,左後ろ足の6種類の足があります。7匹いるので,1種類あたり7本の足があります。全部で足は何本あるでしょう。
正解は,7本×6種類=42 です。
6×7では,7種類の足を持つテントウムシがいることになってしまいます。
順序は、「意味の違い」を表す重要なもの?
いや、「問題文の表現の違い」を表すだけのつまらないものに過ぎない。
(この文章を読んで、私が考えたこと、と言うよりは笑ってしまったこと)
論点がここまで来ると、笑う他ありません。あまりにもふざけた論調に怒りさえ感じます。
「式のたてかたの順序などどうでも良いことなのだ!」ということを、このコメントをした方が、この例を挙げて子供たちに説明する機会を、ぜひ与えたい!
「何それ! 全然わかんない! この人は何を考えているんだろう?」・・・間違いなくそんな感想しか、子どもたちからは出てこないでしょう!
この人の天邪鬼的解釈は、子供だけではなく私でさえ、またこのブログをご覧の多くの方も、???・・・と言った印象を受けるに違いありません。
おまけに、自分自身が記したこの文章に、自分が否定している「式の立て方や順序」(この場合はかけ算)から、解いた人の「考え方の過程が読み取れる」ことの重要性を、結果的に自らが雄弁に語っているではありませんか!極めて支離滅裂で恥ずかしい文面です。

少し前のブログに載せた、テーブルの上においてある蕾のヒヤシンス(水栽培)が、数日前から咲き出しました。
関心のある方は、以下のブログも参考にご覧ください。
マッキーの教育論:ネット評論家の無責任な教育論
マッキーの算数指導法:式のたて方のコメントに応える
マッキーの算数指導法:式のたて方のコメントに応える(2)

![]()
ブログ人気投票にクリックいただけると幸いです!
最初のコメントの後に再び、積分定数さんからコメントを頂きました。
はっきり言ってちょっと無視したい内容も含まれ、感情が交錯した低次元のこうしたネット上の議論を好まない私としては、どうしようかと考えました。
しかし、長年の経験を基にした自分の考えを明確に述べておこうと思い、それが長文になることが予想出来たので、今回は「式のたて方のコメントに応える」その2、次回その3と二回に分けて綴ります。
こうした議論の中で、積分定数さんに対して、いろんな意味で問題視されているといった指摘を受けていますが、その積分定数さんのコメントと、積分定数さんに寄せられたコメントの後に、今回は私の考えを青色の文字で記すことにしましたのでご覧下さい。無論のこと、私の綴った主張は、読んでいただく多くの方に参考になるよう配慮したものです。
(積分定数さんから頂いたコメント)
まず、どう教えるか(方法・手段)、と、何を教えるのか(目的)を分けて考える必要があると思います。
かけ算の順序に拘る教え方をする人、及びそれを擁護する人の多くは、ここを勘違いしている場合が非常に多いです。
算数において何を教えるのかということと、子供たちにその内容を理解させるための教え方は、当然ながら密接に関連したものであり、また教師のそれぞれの学習指導法の主張は、生徒の習熟度・考えの深まりについて責任を持つことを前提として語らなければなりません。
子どもに、しっかりとした式のたて方を指導しきれない教師は、自分の低い教務能力を棚に上げて、恣意的な学習法を子どもに強いるべきではありません。
「かけ算の順序に拘る教え方をする人、及びそれを擁護する人」という対象を示す言い回しは正確ではなく、「考え方を式にしっかりと表すことを指導する教師」と「答えが出せれば式の表記はどうでも良いと考える者」との対比で表すべきで、「かけ算の順序」という焦点をぼかした言い回しは避けなければなりません。
■ そもそもかけ算に順序はない。
■ 「かけ算の順序」は目的ではない。
この2点が明確でない順序指導擁護論は、そもそもその段階で失格だと思っています。
かけ算に順序はないと言っておきながら、かけ算の順序は目的ではないと言っていること自体が意味不明です。
単純に言えば、かけ算を表記した段階で順序が発生するのであって、かけ算はその表記した数字の順序を交換しても答えは一緒になることから、かけ算をその式に従って計算する時点で順序が決まると言って良いでしょう。
もっと例を挙げるなら、文字式の乗法には、アルファベット順という明確な表記順序があり、abcをbacとすれば、中学1年の数学テストでは、バツとなります。・・・かけ算の順序など、どうでもよいだろうとは言えません。
「かけ算の順序は目的ではない?」・・・かけ算の計算を指導する場合、かけ算の順序を変えても答えは同じだということ(交換の法則・小学4年で学習)を指導する場合、「かけ算の順序」が学習目的となります。
順序指導を正当化するには、この2点が明確でなおかつ、教育的メリットが上回るということが示されないとならないと考えます。
>計算のルール、すなわち交換の法則・結合の法則・分配の法則などの決まりと、答えを導き出す考えを表した式の区別
このような区別がなぜ必要なのか分かりません。
式だけで考え方を見ることは不可能だと思います。
式の立て方などどうでもよいだろうという考えを主張する者の多くは、「式だけで考え方を見ることは不可能だ」と言いながら、自分が書いた意味不明な式に、天邪鬼的な意味付けをすることを好むようです。言っていることとやっていることのギャップが甚だしいと言わざるを得ません。
何度も指摘しますが、小学生に問題を出したとき、その問題の解答を導き出した自分の考えの手順を示したものが式です。場合によっては式以外に、与えられた条件の整理や考える手順を示す手段として、線分図・情景図・表・樹形図・面積図・ベン図・てんびん図・文字式など、さまざまなアプローチを試す必要があるでしょう。根気よく解答を導き出していくそのプロセスを式に定着させる(自分の考えを整理する)ことが、算数学習の目的の一つであるはずです。
式がしっかりと書かれていれば、その式を指導者が読み解くことにより、その子がどのように論理的に考え式をたてたのかを、おおよそ知ることができるだけではなく、その式にしたがってその子どもは、自分の考えを他の人に伝えることもできるのです。
算数の学習は、論理的に物事を考え、他の人に分かり易く自分の考えを伝える、そうした力を養うことができるからこそ、大切な教科なのです。
どんなやり方でも良いから答えを出すという主張は、その子のノートに、神のお告げの如く答えだけが書かれていても、「よくできました」と丸をつける算数指導ですが、それでは子どもの考えの深まりは期待出来ません。
(追伸)
どんなやり方でもいいからとにかく答えを出す。
やり方を覚えるのではなくて、試行錯誤して答えに行き着く
というのが大切だと思っています。そのためには、恣意的なルールは極力なくすべきだと思っています。
答えに到る道筋は、さまざまあるでしょう。
勾配が緩やかだけれども時間のかかる道、急坂や危険な隘路だけれども最短でいける道、生徒が集中して解答を求める道を探ることも、算数を学習する重要な目的です。
ただし繰り返し指摘したいのは、乗法公式を覚えずにいつまでも分配の法則を使って計算する(答えは同じ)ことを認めるような、計算の結果だけを求める指導法は、因数分解を学習する時点でその子を頓挫させてしまう結果となることを、教える側は知るべきです。
生徒に対して学習内容を習熟させる役割を担う教師の努力と責任を放棄し、「どんなやり方でもいいからとにかく答えをだしなさい。」は、無責任の誹りを免れません。
塾では、性急に答えだけを出そうとする生徒に対して、「答なんてどうでもいいことでしょう。与えられた条件をしっかりと整理して、ちゃんと式を書いて考えなさい。」と私は指導します。・・・個々の問題の答えをだすことが目的ではなく、問題を解く考えの深まりを期待しているのですから。ただし、公立学校での指導では、そんな過激な言葉は発しませんが。
積分定数さん寄せられたコメント。彼の意見を補完する例として紹介されている。
(事例1)
さっきの算数の問題はこれ→「1.5mのホースの重さは270g、このホースの1mの重さは何g?」 教科書的正解は270÷1.5=180g 長女の考え方は「0.5mで90g、なので1mだと180g」 でもこれだと×になっちゃうんなんだって・・・(・ω・;)。
ありがとうございます!担任の先生もこの単元では×になるけど割り算の計算につながる良い考え方だとほめてくださったようです。「小数の割り算」の単元なので小数の割り算を使わないとダメと言う事なのでしょうね。親バカながらこれからの伸びに期待しています(^^)♪
>「小数の割り算」の単元なので小数の割り算を使わないとダメ
そうであれば、「かけ算の単元だからかけ算を使う」と子供が考えるのは当然。
「教える側が望んだ答案を書くべきだ」というような、子供に空気と行間を読ませることが目的なんだからと、順序を擁護する意見があるが、
「かけ算の単元だからかけ算にする」というのは、まさにそういうことではないのか?
(積分定数さんの主張)
こういう「少数の割り算の単元だから少数の割り算を使わなくてはならない」という、解放の制約が、子供たちが素直に自由に問題に取り組むことを妨げて、「こうやって解くのを先生は認めてくれるだろうか?」という、空気を読む訓練をさせることになってしまっているように思えます。
まず、少数は小数、解放は解法のミスでね。
小5のお子さんだと思われますが、割合の考え方・小数の計算(公立学校小5の学習テーマ)を理解したかどうかをチェックするテストだったと思われます。
答えは確かに正解ですし、答えを導き出そうという努力と工夫した跡が見られる式の立て方であり、当てずっぽうの解き方ではありません。
しかし、「小数計算」と、「割合の式の立て方」のこの子の習熟度は、弱いかまたは判定不能です。
この考え方から読み取れることは、この子は条件を線分図で整理して、その考え方に気づき式をたてたはずです。
その取り組む姿勢を評価すべきか、学習した項目の習熟度の判定としてテストを捉えるべきなのか、教える教師としては、判断に迷うことでしょう。
そうした教師の取り組み(この児童に対しても、しっかりとフォローしている)に思いを馳せることが出来ずに、単純にこの教師の判定を非難する者は、算数指導の全容を理解せず、明らかにクレーマーと断言してよいでしょう。
小数計算も、割合の考え方も習熟しない子どもに、そのことを指摘すること無くゴーサインを出すことが、後々の学習を進める上で、大きな負担をこの子に負わせてしまうことになります。
ここで、私が最近経験したちょっとした例を挙げたいと思います。
ある公立小学校の4年生に、九九を覚えていない生徒がいましたが、無論のこと、小学4年の計算は九九を知らないので、ほとんどできません。
例えば、5×7=え~と、5+5は10,10+5は15,・・・小学2年生なら、その努力を褒めても良いのですが、やはり習得すべき学習項目を習熟しないと、とてもかわいそうな結果となります。
この子は、文章題を出すと論理的なしっかりとした式をたてることができ、九九の習熟が大きなハードルになっていることが分かりました。
そこで、「君ね、1日に1回、トイレの中でも良いから、九九を練習しなさい。必ず覚えられるから!」と言い渡し、およそ1ヶ月後の冬休み明けに、九九をその子に確認すると、嬉しそうにしっかりと九九を言えるようになっているではありませんか。
こうした事例からも、学習すべき項目の習熟を考えずに、答さえ合っていればよいという指導法は、子どもに後々たいへんな負担をかけることになることを、強調しておきます。
また、子どものテストに付けるマル・バツは、そのテスト項目における自分(教える側)の指導評価でもあるのです。
教える立場の者は、そこをいい加減に捉えてはいけません。
児童の学習の習熟度を知り、自分の指導を常に検証し、出てきた結果を、その後の指導に役立てるためにフィードバックする努力をしない教え方は、いつまでも学習内容全体を・鳥瞰・掌握できない人の指導法といえるでしょう。
サザンカは最盛期を過ぎたようですが、陽光が強くなった如月の空に、紅の花が映えていました。
関心のある方は、以下のブログも参考にご覧ください。
マッキーの教育論:ネット評論家の無責任な教育論
マッキーの算数指導法:式のたて方のコメントに応える
マッキーの算数指導法:式のたて方のコメントに応える(3)

![]()
ブログ人気投票にクリックいただけると幸いです!
今朝教室に出ると、以下の私のブログにコメントがありました。今日は、このことについて、綴りたいと思います。
マッキーの教育論:ネット評論家の無責任な教育論
《コメント内容》
5個箱があって、それぞれに10個のクッキーが入っている。クッキーの総数は?この場合、私は5が10個分と自然に思い浮かびますが、5×10とするのは間違いなんでしょうか?
《私の回答》
大人が勝手に答えを考えるのなら、このコメントを寄せた方が言うように、式の立て方など、どうでもよいでしょう。
「クッキーが入ったお菓子箱がa箱あり、それぞれにb個のクッキーが入っているとすると、クッキーの総数は何個でしょう」という問いを、中学1年生の文字式の問題として出題したとします。
b個のクッキーがa箱分だから、b個のa倍で、b×a=a×b=ab(個)とするのが正しい表記法で、考え方をそのまま式に表したba個は、順序が間違っているのでバツとなります。それは、文字式は「交換の法則」をすでに織り込み済みにして、アルファベット順に表記しなければならないからです。
最初の式をたてる場合、アルファベット順を無視して、小学校風に考えの手順通りに式をたて、その後にアルファベット順に書き直すのが一般的な生徒のやり方です。なぜなら、アルファベット順で式をたてる場合、考える手順を表記しているわけではないので、頭の中でアルファベット順に書き直す時に間違えるからです。中学生の学力でさえ、考える手順を式で表し、自分も理解しながら答えを求めることが必要です。
小学校では、「考えた手順を式に表します」が、中学校ではアルファベット順に書きならべることにより、式を美しく見せるという別の側面から出てきたルールにより、「かけ算の順序」が決まります。したがって、文字式の解答には、考えの手順は隠れてしまい、数学的なルールによって出された結果のみしか知ることができません。
このようなことからも、小学校2年生や3年生に、物事を筋道たてて指導する場合は、コメントをされた方の式の立て方は、大きな問題があります。また、積分定数さんの主張を読むと、小学生に対する学習指導経験が無いか乏しいと考えられます。(何度も指摘しますが、大人が答えのみ知りたいなら、式の順序など、どどうでもよいと言って差し支えありません。)
この積分定数さんの問題を、小学校2・3年生に出題するなら、「クッキーが入ったお菓子箱が5箱あり、それぞれの箱には10個のクッキーが入っているとすると、クッキーの総数は何個でしょう。」となります。積分定数さんの問題の「5個箱」は、助数詞を正確に書くと、「5箱」となります。
この方が思いついた5×10という式は、5箱の10個分で50箱となってしまいます。
式を立てて考えを深める学習が重要な小学校低学年では、10個の5箱分(倍)、すなわち10×5=50個と指導しなければなりません。答えが合っていれば、式などどうでもよいだろうという主張は、極めてマズイ結果しか残りません。
繰り返しますが、交換・結合・分配の法則をあたりまえのように使える中学生以上と、数え棒やおはじきなどの算数教材を手で操作しながら考えていく小学校低学年の指導法とは、異なるのも当然です。
「積分定数さん」が、小学校2・3年生に教える場合、5箱×10(倍)=50個?と教える方が良いか、10個×5倍=50個と教える方が子供たちに理解させ易いかを比べてみて下さい。式の立て方などどうでも良いと考えているようですが、単位が入った式で解き方を教えてみて、低学年の子供たちが数値をどのように扱って答えを出すのかを知るべきでしょう。
「この場合、私は5が10個分と自然に思い浮かびますが、5×10とするのは間違いなんでしょうか?」…積分定数さんの問いですが、大人が勝手に浮かんだ考え方を、子どもに教えようとする事自体、大きな勘違いといえるでしょう。
5にはなぜか単位を付けていませんが、この方の式に単位をつけるとすれば、5箱の10個分ということになり、パズルの如く言い訳を駆使しない限り、この式を子どもに説明することができません。こうした主張をする方は、式に意味が無いと言いながら、天邪鬼的に式に意味づけすることが好きなようです。
私がこの質問に応えるとすれば、日頃の私の指導では式の立て方が違っていてもバツとはしませんが、「君ね、答えは合っているけれど、どういった考え方で式をたてたの。」(こういった質問は、小学4年生以上ですけれど)と質問して、筋道たてて応えられたらすんなりとマルをつけるといった対応をしています。
算数の学習の意義は、論理的なものの考え方を鍛えることであり、そして自分の考えを他人に示して、論理的に説明できる力を付けることだと、私は認識しています。決して出題された問題の答えを出すのが目的ではありません。
答えの数値は同じなのだから、どう教えようが良いじゃないか!
自分の考えを、筋道立てて説明する必要があるから、算数嫌いになるのだ!
そう主張する方がいますが、それは大きな間違いです。
「先生、なんで数学なんて勉強するの! 俺、社会に出たら絶対ルートなんか使わないから!」・・・数学嫌いな生徒がよく主張することです。
もしも算数・数学が、答えの正誤が問題にされるだけなら、また式の立て方などどうでもよく、答えに到達すればいいのだと考える指導者は、上記の生徒に対して「全く君の言うとおり!」と応えなければなりません。
(追記)
ネット上で、こうした問題が取り上げられ、議論されていることを調べて知りました。私自身は、こうした場を使って意見を述べたことがないのですが、今回の問題に関して言えば、ネットでは、意見が集約されていくと言うよりも、焦点がぼけて拡散されていく印象を受けます。小学生低学年を指導する現場の実情を無視して、感情的な議論を好むネット中毒者が、深夜に大活躍する議論では、互いの考えが深まりません。残念ながら、「積分定数さん」もこうした範疇に入る人物であることを、何人かの人から後日指摘されました。誠に残念なことです。
プリントを、汚さないでね!・・・と思ったら、ちょっと書かれている英語を読んでね!
関心のある方は、以下のブログも参考にご覧ください。
マッキーの算数指導法:式のたて方のコメントに応える(2)
マッキーの算数指導法:式のたて方のコメントに応える(3)


















