算数の本質

例えば６年生が比を解いていく中で

【3】－４＝【1】＋２

などという式を解いていく場合があるでしょう。

これを大人が見ると、あ、方程式じゃないか、と思いがちなのですが、実はそうではありません。

方程式で考えると、当然、左のー４を右へ、右の【1】を左へと移項することになるわけですが、算数の考え方は



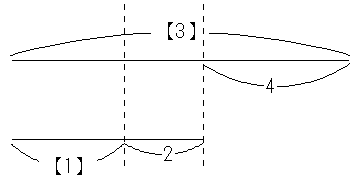
というような線分図を考えたとき、

【3】と【1】の違いである【2】が２＋４＝６と等しいから【1】＝３と解くような考え方なのです。

数学はひとつの考え方から解いていく。移項して、正負の数を考えていくわけですが、小学生はそういうことは知らないから、自分の知っている方法の中で解く。

もちろん、慣れてくれば毎回線分図を描くことはなくなりますが、もとの考え方はそういう工夫なのです。

正方形の面積が196cm2のとき、正方形の1辺の長さを求めなさい。

という問題も、これは数学でいえば二次方程式かもしれない。

しかし、196＝２×98＝２×２×49＝２×２×７×７　と分解できるから1辺の長さは14cmと求めるわけで、その工夫を考えるのが算数だといっていい。

数学を知れば、もっと考える道具が増えるかもしれないが、算数はその道具を限ってその代わり、それをいかに使うか、ということを考えさせようとします。

だから、中学入試の問題を大学生が解くと解けなくなる場合があるわけです。これは大学生ができないからではなく、「そういう考え方に慣れていない」だけのことです。

限られた道具立ての中からどうやって問題を解けばいいか工夫する。図を描いてもいい、表を作ってもいい、あるいはグラフを考えてもいいかもしれない。

全部書き出しちゃう、という手にでて、そのうち規則が見つかる場合だってあるでしょう。

入試は時間が限られるし、合格点はとらなければいけないから、つい道具立てを増やす方向に行きがちですが、しかし、道具を増やせば実は子どもたちがマスターしなければいけないことが増えてしまう分、子どもは算数の本質にたどり着く前にくたびれてしまうということがおきる可能性があるのです。

中学校の先生は、小学生の知っていることだけで解ける問題を作ろう、ということで作問をします。逆にこれを知らないとできない、というようなことはすべて問題に書いてしまわなければいけないという条件が付いています。

だからそこは信頼して、子どもたちの知っていることだけで、どうやって問題を解けばいいか、ということに集中する方が、結局算数はできるようになると私は思います。

=============================================================
今日の田中貴.com

後半戦へ
==============================================================
中学受験　算数オンライン塾

8月17日の問題
==============================================================






にほんブログ村