最短路問題: 双方向探索(bidirectional search) - 1

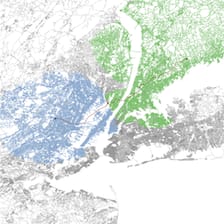
前回の記事で登場した双方向探索(bidirectional search)を説明していく。

まずは、通常のダイクストラ法から復習する。P2P最短路問題の終了条件は「終点が探索点となる」ことであり、それまでひたすら幅優先探索的に探索済み範囲を広げていく。

「両方向探索」では、通常のダイクストラ法を２つ同時に走らせるだけのように感じるかもしれないが、その終了条件が多少複雑かもしれない。もちろん単に forward, backward の両方で確定済みになったらではない。

forward, backward それぞれのポテンシャルの更新時に、求めるべきパスの長さの更新を行う。そのパスが更新できなくなれば終了となる。

Df(v)  : forward-search におけるポテンシャル(始点からの距離)
Db(v)  : backward-search におけるポテンシャル(終点からの距離)
Qf(v)  : forward-search における優先キュー
Qb(v)  : backward-search における優先キュー
l(v,w) : 枝 v-w の重み
mu     : 求めるパスの長さ
muid   : forward-search と backward-search をつなぐ点

/* forward-search でのポテンシャル更新 */
if ( Df(v) + l(v,w) < Df(w) ) {
    Df(w) = Df(v) + l(v,w);
    if ( Df(v) + l(v,w) + Db(w) < mu ) {
        mu = Df(v) + l(v,w) + Db(w);
        muid = w;
    }
}

/* backward-search でのポテンシャル更新 */
if ( Db(v) + l(v,w) < Db(w) ) {
    Db(w) = Db(v) + l(v,w);
    if ( Db(v) + l(v,w) + Df(w) < mu ) {
        mu = Db(v) + l(v,w) + Df(w);
        muid = w;
    }
}

/* 終了条件 */
if ( Qf[root] + Qb[root] >= mu ) {
  return (mu, muid);
}

また「両方向探索」では終点からも同様の探索を行う事になるため、グラフ表現や優先キューが forward 側だけではなくて backward 側分も必要となる。よって、これまでと同じレベルの探索速度を保ちたければ通常の倍のメモリが必要になるだろう。