湿度の問題１ グラフを使う

　＊11/6 タイトルを修正しました！

中学生の中間テストが終わったと思ったら今日は大変寒いです。
もう冬なんですかね‥

テスト範囲に湿度があったのですが
湿度が苦手な生徒が多いですね。
なので、ネットで見つけた問題を解説していきます。

その前に、「湿度」とは何か、をおさらいしておきましょう。
まあ、空気の湿り気のことなんですが、単位が「％」なので割合なんですね。
　その温度の空気１㎥中の飽和水蒸気量に対して、何倍の水蒸気が含まれているか
が湿度です。

なので、「湿度２０％」は、「目一杯の水蒸気量の０.２倍」
ということになります。


問題１　グラフの曲線は飽和水蒸気量を表している。また、青い棒グラフは気温25℃の空気に含まれている水蒸気を表している。次の問いに答えよ。
　

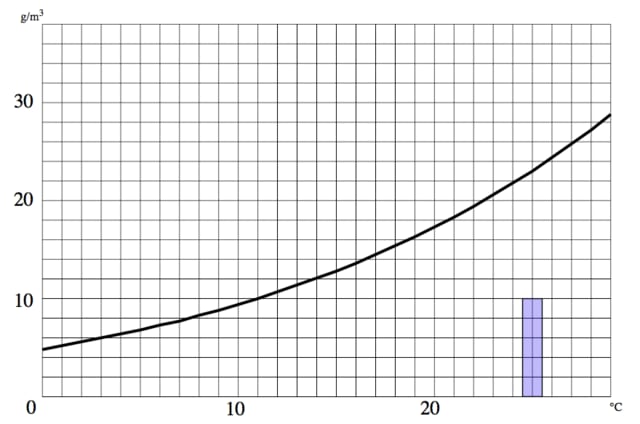
　はい、ここでまずグラフをきちんと読み取りましょう！
　グラフの縦軸、横軸をきちんと確認しますよ！
　
　横軸は単位が「℃」となっていて、問題文に「気温25℃の‥」とあることから「気温」を表していて、
　１目盛りは１℃ですね。
　縦軸は単位が「g/㎥」となっていて、問題文に「青い棒グラフは‥水蒸気量を表している」とあることから「水蒸気量」を表していて、
　１目盛りは２g/㎥ですね。
　グラフをきちんと読み取れたら、設問を読みます。


(1) この空気25℃での湿度を求めよ。（割り切れない場合小数第１位を四捨五入せよ）

　湿度を求める時にはこの公式を暗記したと思うのですが、

　
　上にも書いた通り湿度は割合ですので、

　　含まれている水蒸気量 ÷ 飽和水蒸気量

　で計算して％に直した方が早いです。

　25℃は青いグラフですから、気温25℃のときに含まれている水蒸気量は、グラフから10g/㎥、


　25℃の飽和水蒸気量は、グラフから23g/㎥

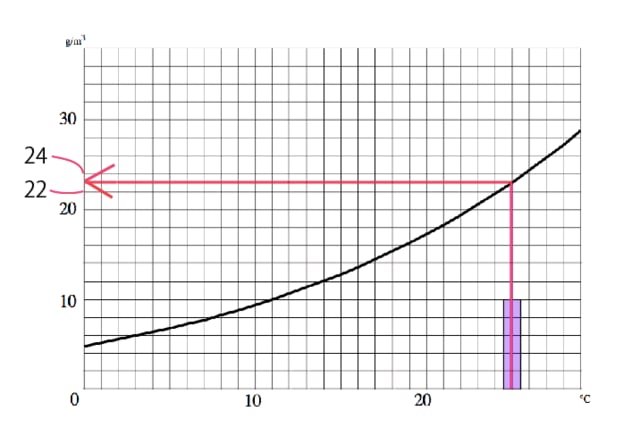
　と読み取れますね。

　　　１０ ÷ ２３ ＝０.４３４７‥ →４３.４７‥％
　　小数第１位を四捨五入なので　　　　　　　　　　　　　　　　　　　　　　　　　４３％　

　グラフをきちんと読み取って、計算すれば、結構簡単ですね！


(2) この空気の露点を求めよ。

　「露点」の意味をしっかり理解していれば楽勝ですね！
　露点とは、含まれている水蒸気が冷やされて水として出てきちゃう温度のことです。
　つまり、このとき含まれている水蒸気量が飽和水蒸気量になる温度が露点なんですね。
　グラフを見ると‥

　１１℃とわかりますね！　　　　　　　　　　　　　　　　　　　　　　　　　　　　１１℃

この調子でラスト問題です！

(3) 空気中の水蒸気量を変えずにこの空気の温度を下げる。
　３℃まで下げた時、空気１㎥中にどれだけの水滴ができるか求めよ。

　なんだかややこしそうですが、大丈夫です！
　気温が下がったので、空気中に含むことのできる水蒸気量は減ります。
　３℃ではどのくらいまで含むことができるか、飽和水蒸気量をグラフで見ると‥

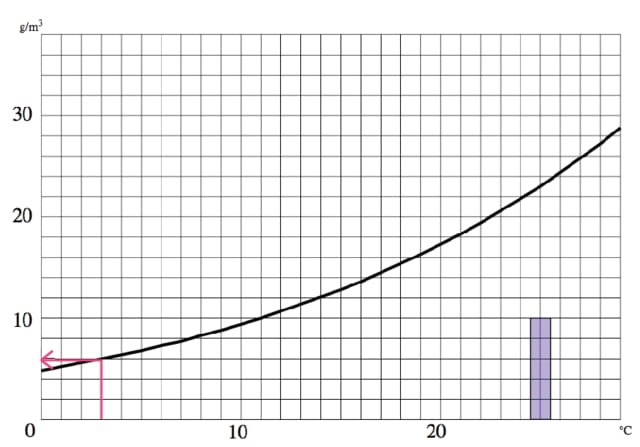
　６g/㎥ですね！
　３℃では１㎥中に６gしか水蒸気は含むことができないのです。
　今の水蒸気量は(1)で読み取った通り１０g/㎥ですから多い分は水になってしまうわけです。
　　１０−６＝４　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ４g


どうでしょうか？
言葉の意味と計算の仕方、グラフの読み取りが理解できたでしょうか？
露点ってのは目一杯のときの温度か、
湿度は今の水蒸気量を飽和水蒸気量でわればいいんだ、
てな辺りがわかれば、あとは練習をしてくだけです！

次回は表を使った計算をします。