【能力開発】図形センスを磨き、難問に挑む－高校への数学「レベルアップ演習」編§７－

　中学の時、図形問題が苦手であると、高校、大学入試時まで引きずってしまうことがある。

　そして、図形問題を解くセンスは、知覚・認知過程の変容も必要となるため、短期間では、なかなか容易に身に着けることはできない。

　難関大学の入試において図形問題が出ることから、早期に着手して苦手意識を克服し、図形力をUPしておくことが望まれる。

　ここで、まずは東京出版の「高校への数学」の別冊では登竜門的な位置付けである、「レベルアップ演習」に取り組み、図形問題を解くセンスを身に着けていきたい。

❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋

【★７・１】（すべては直角と平行線から始まった…）
（問題文は当該問題集を参照して下さい）【この本へのリンク】

　この問題自体は、息子・娘ともに瞬殺で解いてしまい、かなり平易なものだったが、関連してあれこれ考えだすと、とても深みにはまりこんでしまった。

【問題の解法の流れ】

「三角形の外角の定理（内対角の和は外角に等しい）」
　　↓
　ｘ＋１５°＝１１０°、４０°＋ｙ＝ｘ
　より、ｘ、ｙを求めてO.K.

　もしそれが思い浮かばなくても

「三角形の内角の和は１８０°（２∠Ｒ）の定理」
　↓
　ｘ＋１５°＋a＝１８０°
　１１０°＋a＝１８０°
　４０°＋ｙ＝ｘ
　より、a、ｘ、ｙを求めてO.K.


●しかし、問題は、「三角形の内角の和は１８０°（２∠Ｒ）の定理」の証明について突き詰めて考えていくことから始まって行った。

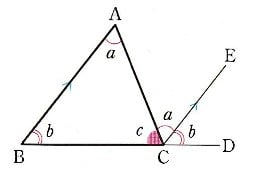
　まず、「三角形の内角の和は１８０°（２∠Ｒ）の定理」（Ｒは「直角」（right angleの頭文字）を表す）であるが、以下の手順で証明する。

（step１）
　下図の三角形ABCにおいて、辺ABに対する平行な補助線CEを引いて、
　「平行線の錯角は等しいという定理」と「平行線の同位角は等しいという定理」を適用し、
その補助線CEの周りに三角形の各角を集める。
　↓
（step２）
　集めた∠BCA＋∠ACE＋∠ECDは底辺BCDの角と等しく、
「直線上の角１８０°（２∠Ｒ）に等しいという定理」と一致。

（了）

【図】



+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-:+:-+:-+:-+:-+:-+

　ここまではよかったのだが・・・

●そこで、さらに突き詰めると、「平行線の錯角は等しいという定理」と「平行線の同位角は等しいという定理」は、「ユークリッド原論」（以下「原論」という）に命題２９（定理）があるが、どのように証明するかということである。

　「対頂角は等しい」ということが示されていると、「錯角」と「同位角」は、それぞれ等しいことになる。
　よって、「平行線の錯角は等しい」ということが示せれば、「平行線の同位角は等しい」ということが導ける。

●最初に、「対頂角は等しいという定理」を証明したいのだが、
　そのためには、その前の段階があって、

　「直線上の角は１８０°（２∠Ｒ）」という、「原論」の命題１３（定理）が必要となる。

　それを以下のように証明する。

　【下図】において、



　①もし、∠DBA＝∠ABCならば、∠DBA＝∠ABC＝∠R（「原論」定義１０より）

　②もし、∠CBA≠∠ABDならば、

　∠CBE＝∠EBD＝∠Rとなる垂線を引く。

　∠EBD＝∠R＝∠EBA＋∠ABD

　∠CBE＋∠EBD＝２∠R＝∠CBE＋∠EBA＋∠ABD
　よって、∠EBA＋∠ABD＝∠R

　一方、∠CBA＋∠ABD＝∠CBE＋∠EBA＋∠ABD
　∠CBE＝∠R、∠EBA＋∠ABD＝∠Rより、
　∠CBA＋∠ABD＝２∠R

（了）

●続いて、「対頂角は等しいという定理」を次の手順で証明する。

　【下図】において、



　∠DEA＋∠AEC＝２∠R（命題１３より）

　∠AEC＋∠CEB＝２∠R（命題１３より）

　∠DEA＋∠AEC＝∠AEC＋∠CEB

　両辺から∠AECを引くと、対頂角同士は、∠DEA＝∠CEBとなる。

　同様に、∠DED＝∠AECが示される。

●ようやく、「平行線の錯角は等しいという定理」の証明を行っていく。

　そのためには、「原論」の第1巻にある、「第５公準」と、先に証明した「直線上の角は１８０°（２∠Ｒ）」という命題１３（定理）を用いることになる。

　「公準」とは、数学上の言葉で、証明の出発、前提の要請（命題）となるものだ。

　これは一般的に自明なものとして使用するものだ。

　そして、「原論」の「第５公準」は、
　「１直線が２直線に交わり同じ側の内角の和を２直角より小さくするならば、この２直線は限りなく延長されると２直角より小さい角のある側において交わること」
だ。

●「平行線の錯角は等しいという定理」の証明は、背理法（高校数学で学ぶ）を使う。

【図】



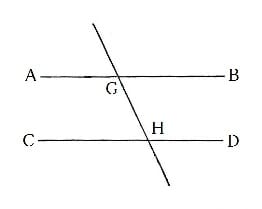
（step１）２つの直線ABと直線CDが平行である時、図の「錯角である∠AGHと∠DHGが等しくない」（∠AGH≠∠DHG）と仮定する。結果、どちらかの角が大きいことになるが、仮に∠AGH＞∠DHG…①とする。
　　↓
（step２）①の両辺に∠BGHを加えると、∠AGH＋∠BGH＞∠DHG＋∠BGHとなる。
　　↓
（step３）∠AGH＋∠BGHは直線上の角で、上記の「命題１３」より、２∠Rとなる。
　　↓
（step４）よって、∠DHG＋∠BGH＜２∠Rとなる。
　　↓
（step５）「第５公準」より、直線ABと直線CDは交わることになる。
　　↓
（step６）このことは、直線ABと直線CDは平行であることに矛盾する。
　　↓
（step７）結局、「錯角の∠AGHと∠DHGが等しくない」という仮定は誤りとなり、２つの直線が平行な時は、「その錯角は等しい」ことになる。

（了）

●しかし、話はここで終わらない・・・（ユークリッド幾何学を超えて）

　以上に見たように、
　「三角形の内角の和は１８０°（２∠Ｒ）の定理」は、「原論」の「第５公準」を前提とした場合に成り立つ。

　では、この「第５公準」を前提としない場合や、成り立たない場合は、「三角形の内角の和」はどうなるのだろうか？

　そして、その場合、どういった幾何学になるのだろうか？

　結論を言うと、それは「原論」で展開される「ユークリッド幾何学」というものに対し、「非ユークリッド幾何学」というものになる。

　「第５公準」が成り立たない場合である「非ユークリッド幾何学」においては、３次元球面上では「三角形の内角の和は２７０°」となったり、負に曲がった平面上では「三角形の内角の和は１８０°以下」となる。

【非ユークリッド幾何学】の発見まで

「第５公準」は他の公準に比べ、表現が複雑
　　↓
「第５公準」は定理であり、これ自体が証明可能？
　　↓
　2000年間の証明の試み
　　↓
「第５公準」⇔同値「三角形の内角の和が２直角に等しい」（ルジャンドル）

「第５公準」の否定⇔同値「三角形の内角の和が２直角より真に小さい」（サッケリの理論より）
　　↓
「非ユークリッド幾何学」の発見（ガウス、ボヤイ、ロバチェフスキー、関連してリーマン）

【今回参考にした図書】
・「ユークリッド原論追補版」共立出版（2011/5/25）
・「ユークリッド『原論』とは何か―二千年読みつがれた数学の古典」斎藤憲：岩波書店（2008/9/17）
・「現代幾何学の流れ」砂田利一：日本評論社（2007/10）

【最後に】

　普段、当たり前に受け取っていた物事や知識などについて、改めて原点に立ち返って突き詰めて確認してみたことは、思った以上に大変だった・・・

　今後も図形問題を解くにあたっては、「原論」を随時参照して、立ち返って考えて行きたい。

　※なお、各定理の証明は、「原論」の記載通りに再現せずに、自分なりにアレンジした。

❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋❋

≪他のページ≫
★高１駿台模試（第１回：H25.6.9）
★高２駿台模試（第１回：H26.6.8）

★現代文勉強法の考察～各問題集を巡って～【田村のやさしく語る現代文】編
★【現代文の勉強法01】要約力、文章構造分析力、アイデア創造の発問力の強化－日本語能力試験N２編(1)　問題10(1)

★【システム英単語勉強法】６００語を２０日間で記憶するためにエクセルを活用した覚え方
★【英語多読】目指せ！大学受験の英文読解で１００万語！

★【大学への数学1対1対応の演習】の使い方・勉強法－直観力鍛錬と問題構造分析－数学Ⅰ数と式　例題８
★【能力開発】図形センスを磨き、難問を制覇する－高校への数学「レベルアップ演習」編§７合同＆線分比・面積比－

★美術展・街歩きのページ

★私の読書メーター（全記録）

★読書日記（受験本）

★ウェブ記事セレクション（H27.1～）
★ウェブ記事セレクション（H26.6～12）
★ウェブ記事セレクション（H26.1～6）