昆虫の呼吸-その10 改訂版
Weis-Fogh(ヴァイスフォー)の論文を再度読み直して空孔率を訂正し、計算をやり直しました。
前回は昆虫の外骨格の強度という点で、怪獣のような巨大化は難しいという話でした。
今回は、気管の分布から巨大化が可能かどうか考えてみます。
「昆虫の呼吸-その7」ではWeis-Fogh(ヴァイスフォー)の論文を話題にしました。それによると飛翔筋内の気管の構造は、気門―1次気管(直径100~μm)-2次気管(7~1μm)―3次気管(2.5~1μm)―毛細気管(1~0.1μm)と分岐します。1次気管から毛細気管までは約1mmです。
1次気管から毛細気管までの気管系の分岐の様子:
2次気管から約25本の3次気管が分岐して、3次気管から20~30本の毛細気管が分岐します。
従って2次気管1本から500~750 本の毛細気管が分かれて、筋肉細胞へ繋がっている。
飛翔筋の断面積に対する気管系の断面積の割合を空孔率(H)といい、これには1次気管から毛細気管まですべて含み、バッタでは約7%、トンボでは1次だけで1-4%。
このことから、飛翔筋の空孔率Hが1%から7%の間にあるときに、筋肉では酸素の供給と二酸化炭素の排出が適切に調節されるとします(仮定1)。従って巨大化する昆虫では空孔率Hは巨大化前後で同じ値をとることになります。

翅の挙上筋1本を考える。その横断面の面積をAoとする
その面を通る1次気管支の数をm1、断面積をS1とし、2次、3次気管支、毛細気管についても数と断面積をそれぞれm2、S2、m3,S3、m4、S4とします。
気管系の総数Mt=m1+m2+m3+m4
全気管系の断面積Stは
St=S1m1+S2m2+S3m3+S4m4 (1)
空孔率H= St/Aoは1%~7%の間なので
0.01≦St/Ao≦0.07
昆虫が巨大化して相似形のまま体長が元のn倍になったとすると体積はnの3乗倍になりますが、体を構成する筋肉細胞の大きさは同じと考えられるので、細胞の数も元のnの
3乗倍になる。 従ってその細胞に繋がる毛細気管の数m4もnの3乗倍のm4✕n^3になります。
1次気管から毛細気管までの直径は巨大化後も同じサイズで、気管系の数は全てn^3倍になるとすると(仮定2)、
巨大化後の気管系の総断面積Snは
Sn=(S1m1+S2m2+S3m3+S4m4)・n^3
筋の断面積はnの2乗で拡大するのでAo ・n^2になる。従って巨大化後の空孔率Hnは
Hn=Sn/(Ao ・n^2)=(S1m1+S2m2+S3m3+S4m4)・n/Ao
(1)より
Hn=(St/Ao)・n
仮定1からHnも1%~7%の間とすると
0.01≦(St/Ao)・n≦0.07 ここに0.01≦St/Ao≦0.07 (2)
となる。これを満たすSt/Aoとnが巨大化の指標となります。
例1 5倍の巨大化 n=5では(2)より
0.01≦(St/Ao)・5≦0.07
従って
0.002≦(St/Ao)≦0.014
となります。
これは例えばH=(St/Ao)=0.012であれば(2)を満たすのでこの巨大化は可能です。
例2 10倍の巨大化 n=10では 同様にして
0.001≦(St/Ao)≦0.007 となるが、これは仮定1から(St/Ao)が0.01以上なので満たされない。従って10倍の巨大化は不可能です。
この場合Hn=10×(St/Ao)なので、H=(St/Ao)が最小の0.01でも巨大後はHn=0.1、従って空孔率が10%となり7%以下でなくなります。
巨大化後には筋肉細胞数が巨大化率の3乗で増えるため、気管系の量も増えてそれが筋肉を減少させるために巨大化に限界があるということになります。

この図は(2)式が0.01と0.07の間の時に、St/Aoとnが取り得る範囲を示したもので、オレンジ色の部分の範囲です。
空孔率Hが1%~7%の制限では、巨大化率n=7が最大であり、巨大化の限界であることを示しています。これ以上の巨大化は、n=10の場合のように気管系の筋肉内に占める割合が7%を越えることになります。
以上から、仮定1と2のもとでは、気管系をもつ昆虫では巨大化には上限があって、この場合はそれが7倍ということになります。
前回は体長8cmのバッタを例に挙げたので、8x7=56cmが上限となります。
古生代後半に生息していた巨大トンボ:メガネウラの体長は約30cmあったとのことですが、ここで予測した巨大化の範囲に収まっています。
石炭紀からペルム紀にかけての1億年間(3.5~2.5億年前)には酸素濃度が現在の20%よりも高く、最高で35%まで上昇したことが知られています(昆虫の呼吸-その4参照)。
酸素濃度と巨大化の関連については諸説あって今もなお議論が続いています。しかし、ここで検討したように巨大化による細胞数の増加は同時に気管系も増加させるので、筋肉内の著しく増加した気管系の量が必要な筋肉を減少させることにつながります。気管呼吸をする昆虫では巨大化に上限があると考えられます。
前回の話題に出てきた、体長4mの怪獣のような巨大昆虫は気管呼吸をしている限り不可能のようですね。
仮定1の検討
「気管系の断面積の合計は飛翔筋の断面積の1%以上7%以下である」という仮定は観察結果です。
飛翔筋内の気管系が少なければ十分にガス交換ができません。また気管系の占める割合が多ければそれだけ筋肉の量が減ることになります。空孔率が1%から7%の観察結果がすべての昆虫に当てはまるのかどうかはわかりませんが、この空孔率は妥当な割合だと考えてこれを仮定しました。
仮定2について
「気管系の直径が巨大化前と同じで、その本数だけがnの3乗倍になる」
細胞と直接繋がる毛細気管の直径は筋肉細胞の大きさに規定されるのでn倍の巨大化前と同じはずですが、毛細気管と気管の長さは巨大化に比例してn倍に延長するでしょう。酸素や二酸化炭素の拡散量(供給量)は距離に反比例して減少します。また、筋肉細胞数はnの3乗に比例して増えるので酸素消費量もそれだけ増加します。
つまり気管系の延長で酸素供給量は減るにもかかわらず、全細胞での必要とする酸素量は増加するという状況になります。
必要な酸素を供給するためには、昆虫体の筋肉の収縮と弛緩による気管換気回数の増加(昆虫の呼吸―その3)とともに気管系を太くして体積を増やして酸素濃度の変化を安定させる必要があります。
こう考えると、細胞に貫入する毛細気管以外の気管系の直径は大きくなると推測されますが、ここでは直径は巨大化前と同じで本数だけが増えることとして、巨大化に有利なままにしています。
参考文献
1.Weis-Fogh T. J Exp Biol 41: 229-56, 1964
2.ピーター・D・ウオード 恐竜はなぜ鳥に進化したのか 文藝春秋 2008
Weis-Fogh(ヴァイスフォー)の論文を再度読み直して空孔率を訂正し、計算をやり直しました。
前回は昆虫の外骨格の強度という点で、怪獣のような巨大化は難しいという話でした。
今回は、気管の分布から巨大化が可能かどうか考えてみます。
「昆虫の呼吸-その7」ではWeis-Fogh(ヴァイスフォー)の論文を話題にしました。それによると飛翔筋内の気管の構造は、気門―1次気管(直径100~μm)-2次気管(7~1μm)―3次気管(2.5~1μm)―毛細気管(1~0.1μm)と分岐します。1次気管から毛細気管までは約1mmです。
1次気管から毛細気管までの気管系の分岐の様子:
2次気管から約25本の3次気管が分岐して、3次気管から20~30本の毛細気管が分岐します。
従って2次気管1本から500~750 本の毛細気管が分かれて、筋肉細胞へ繋がっている。
飛翔筋の断面積に対する気管系の断面積の割合を空孔率(H)といい、これには1次気管から毛細気管まですべて含み、バッタでは約7%、トンボでは1次だけで1-4%。
このことから、飛翔筋の空孔率Hが1%から7%の間にあるときに、筋肉では酸素の供給と二酸化炭素の排出が適切に調節されるとします(仮定1)。従って巨大化する昆虫では空孔率Hは巨大化前後で同じ値をとることになります。

翅の挙上筋1本を考える。その横断面の面積をAoとする
その面を通る1次気管支の数をm1、断面積をS1とし、2次、3次気管支、毛細気管についても数と断面積をそれぞれm2、S2、m3,S3、m4、S4とします。
気管系の総数Mt=m1+m2+m3+m4
全気管系の断面積Stは
St=S1m1+S2m2+S3m3+S4m4 (1)
空孔率H= St/Aoは1%~7%の間なので
0.01≦St/Ao≦0.07
昆虫が巨大化して相似形のまま体長が元のn倍になったとすると体積はnの3乗倍になりますが、体を構成する筋肉細胞の大きさは同じと考えられるので、細胞の数も元のnの
3乗倍になる。 従ってその細胞に繋がる毛細気管の数m4もnの3乗倍のm4✕n^3になります。
1次気管から毛細気管までの直径は巨大化後も同じサイズで、気管系の数は全てn^3倍になるとすると(仮定2)、
巨大化後の気管系の総断面積Snは
Sn=(S1m1+S2m2+S3m3+S4m4)・n^3
筋の断面積はnの2乗で拡大するのでAo ・n^2になる。従って巨大化後の空孔率Hnは
Hn=Sn/(Ao ・n^2)=(S1m1+S2m2+S3m3+S4m4)・n/Ao
(1)より
Hn=(St/Ao)・n
仮定1からHnも1%~7%の間とすると
0.01≦(St/Ao)・n≦0.07 ここに0.01≦St/Ao≦0.07 (2)
となる。これを満たすSt/Aoとnが巨大化の指標となります。
例1 5倍の巨大化 n=5では(2)より
0.01≦(St/Ao)・5≦0.07
従って
0.002≦(St/Ao)≦0.014
となります。
これは例えばH=(St/Ao)=0.012であれば(2)を満たすのでこの巨大化は可能です。
例2 10倍の巨大化 n=10では 同様にして
0.001≦(St/Ao)≦0.007 となるが、これは仮定1から(St/Ao)が0.01以上なので満たされない。従って10倍の巨大化は不可能です。
この場合Hn=10×(St/Ao)なので、H=(St/Ao)が最小の0.01でも巨大後はHn=0.1、従って空孔率が10%となり7%以下でなくなります。
巨大化後には筋肉細胞数が巨大化率の3乗で増えるため、気管系の量も増えてそれが筋肉を減少させるために巨大化に限界があるということになります。

この図は(2)式が0.01と0.07の間の時に、St/Aoとnが取り得る範囲を示したもので、オレンジ色の部分の範囲です。
空孔率Hが1%~7%の制限では、巨大化率n=7が最大であり、巨大化の限界であることを示しています。これ以上の巨大化は、n=10の場合のように気管系の筋肉内に占める割合が7%を越えることになります。
以上から、仮定1と2のもとでは、気管系をもつ昆虫では巨大化には上限があって、この場合はそれが7倍ということになります。
前回は体長8cmのバッタを例に挙げたので、8x7=56cmが上限となります。
古生代後半に生息していた巨大トンボ:メガネウラの体長は約30cmあったとのことですが、ここで予測した巨大化の範囲に収まっています。
石炭紀からペルム紀にかけての1億年間(3.5~2.5億年前)には酸素濃度が現在の20%よりも高く、最高で35%まで上昇したことが知られています(昆虫の呼吸-その4参照)。
酸素濃度と巨大化の関連については諸説あって今もなお議論が続いています。しかし、ここで検討したように巨大化による細胞数の増加は同時に気管系も増加させるので、筋肉内の著しく増加した気管系の量が必要な筋肉を減少させることにつながります。気管呼吸をする昆虫では巨大化に上限があると考えられます。
前回の話題に出てきた、体長4mの怪獣のような巨大昆虫は気管呼吸をしている限り不可能のようですね。
仮定1の検討
「気管系の断面積の合計は飛翔筋の断面積の1%以上7%以下である」という仮定は観察結果です。
飛翔筋内の気管系が少なければ十分にガス交換ができません。また気管系の占める割合が多ければそれだけ筋肉の量が減ることになります。空孔率が1%から7%の観察結果がすべての昆虫に当てはまるのかどうかはわかりませんが、この空孔率は妥当な割合だと考えてこれを仮定しました。
仮定2について
「気管系の直径が巨大化前と同じで、その本数だけがnの3乗倍になる」
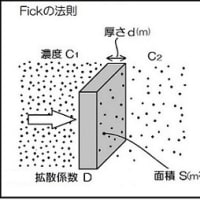
細胞と直接繋がる毛細気管の直径は筋肉細胞の大きさに規定されるのでn倍の巨大化前と同じはずですが、毛細気管と気管の長さは巨大化に比例してn倍に延長するでしょう。酸素や二酸化炭素の拡散量(供給量)は距離に反比例して減少します。また、筋肉細胞数はnの3乗に比例して増えるので酸素消費量もそれだけ増加します。
つまり気管系の延長で酸素供給量は減るにもかかわらず、全細胞での必要とする酸素量は増加するという状況になります。
必要な酸素を供給するためには、昆虫体の筋肉の収縮と弛緩による気管換気回数の増加(昆虫の呼吸―その3)とともに気管系を太くして体積を増やして酸素濃度の変化を安定させる必要があります。
こう考えると、細胞に貫入する毛細気管以外の気管系の直径は大きくなると推測されますが、ここでは直径は巨大化前と同じで本数だけが増えることとして、巨大化に有利なままにしています。
参考文献
1.Weis-Fogh T. J Exp Biol 41: 229-56, 1964
2.ピーター・D・ウオード 恐竜はなぜ鳥に進化したのか 文藝春秋 2008
























※コメント投稿者のブログIDはブログ作成者のみに通知されます