前記事では、肝となるアルゴリズムに絞って書いたが、今回は insert の全体像を。
そのためにいくつかの準備が必要である。
■準備■
・点 v に対し「c(v) = 最小枝長」とする。枝がない場合は「c(v) = infinity」。
・点 v に対し、d(v) はポテンシャル値。
・バケットを補助する集合 F を用意する。
・「μ = 最後に取り出したポテンシャル値」とする。
(1レベルのように、mod bucket_size でなく、素のポテンシャル値)
■点 u を挿入する
if (μ + c(u) >= d(u)) {
F に u を挿入する
}
else {
(i,j) の組をビット演算で求めて、u を B(i,j) に挿入する
}
そのためにいくつかの準備が必要である。
■準備■
・点 v に対し「c(v) = 最小枝長」とする。枝がない場合は「c(v) = infinity」。
・点 v に対し、d(v) はポテンシャル値。
・バケットを補助する集合 F を用意する。
・「μ = 最後に取り出したポテンシャル値」とする。
(1レベルのように、mod bucket_size でなく、素のポテンシャル値)
■点 u を挿入する
if (μ + c(u) >= d(u)) {
F に u を挿入する
}
else {
(i,j) の組をビット演算で求めて、u を B(i,j) に挿入する
}












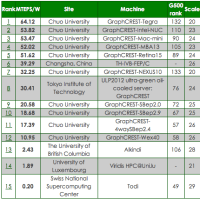
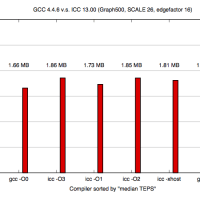
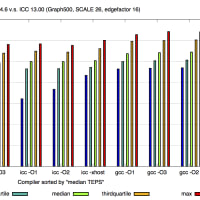
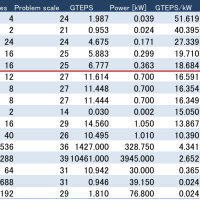
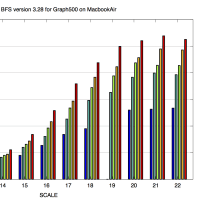
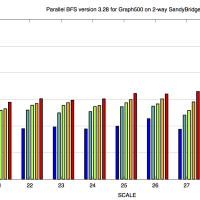
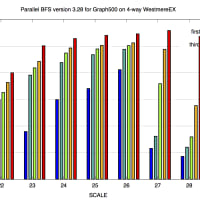
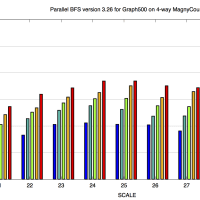
※コメント投稿者のブログIDはブログ作成者のみに通知されます