ある授業で「分枝限定法」について発表することになったので、
ナップサック問題を解くソルバーを作ってみた。
それにしても、なんてアバウトなテーマなのかと思ってしまう。
全列挙法や、ラグランジュ緩和を用いた分枝限定法、
また更に釘つけテストを適応したものと3つ作ってみた。
1.全列挙法
とりあえず、すべての解を列挙。最適値を保存しておく。
2.ラグランジュ緩和による分枝限定法
線形緩和問題を解き、その値と現在までの上界値を欲張り法により算出。
効率の良い順に探索しておけば何もしないときに比べ、
早い段階で最適解が求まる可能性が高いので途中で止められる。
3.枝付けテストを用いた分枝限定法
変数の多い問題を解く際に、実際には意味のない変数を前処理を行って見分け、取り除く。
各変数を固定して(釘付けして)分枝限定法を行う。
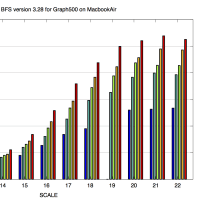
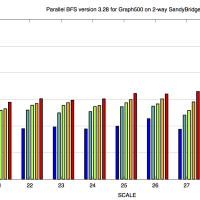
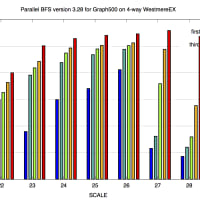
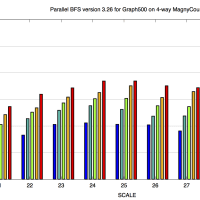
実行時間は 1>2>3 となり、まあうまくいっていると言えるだろう。
ただ小さな問題であると、動的確保したメモリを用いると処理が遅くなってしまう。
全列挙法などでは、たかだか30程のアイテムでも待つことになるので、
静的にとってしまった方がよいだろう。
ナップサック問題を解くソルバーを作ってみた。
それにしても、なんてアバウトなテーマなのかと思ってしまう。
全列挙法や、ラグランジュ緩和を用いた分枝限定法、
また更に釘つけテストを適応したものと3つ作ってみた。
1.全列挙法
とりあえず、すべての解を列挙。最適値を保存しておく。
2.ラグランジュ緩和による分枝限定法
線形緩和問題を解き、その値と現在までの上界値を欲張り法により算出。
効率の良い順に探索しておけば何もしないときに比べ、
早い段階で最適解が求まる可能性が高いので途中で止められる。
3.枝付けテストを用いた分枝限定法
変数の多い問題を解く際に、実際には意味のない変数を前処理を行って見分け、取り除く。
各変数を固定して(釘付けして)分枝限定法を行う。
実行時間は 1>2>3 となり、まあうまくいっていると言えるだろう。
ただ小さな問題であると、動的確保したメモリを用いると処理が遅くなってしまう。
全列挙法などでは、たかだか30程のアイテムでも待つことになるので、
静的にとってしまった方がよいだろう。












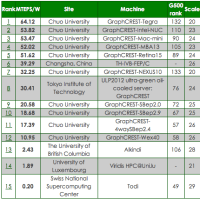
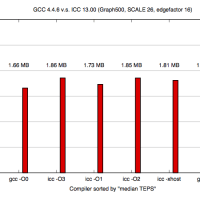
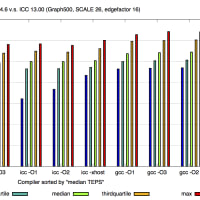
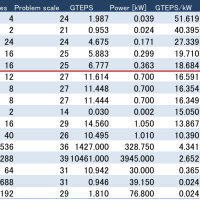
※コメント投稿者のブログIDはブログ作成者のみに通知されます