バケット法 (Dial's implementation) では、探索候補ノードの順番を最大枝長分の配列 bucket[max_length] と、両方向リストによって保持している。bucket[] は、循環リスト(circularly-linked list)であるので、次の要素を参照するときに、次のような演算を多用する。(bucket_size == max_length である)
i = (i + 1) % bucket_size;
バケット法では距離分だけ上記の演算をする(全米データ1対全では 4000万~5000万回ほど)ため、除算のコストがばかにならない。以下のように if 文に書き直すことで改善できる。
i++;
if (i >= bucket_size) i = 0;
また、bucket_size が2のべき乗であるならば、さらに改善できるようなので、bucket[] を切り上げて使用するというのも手のなのかもしれない。
アクセスパターン解析と並行して演算の再確認をしておこうと思う。
i = (i + 1) % bucket_size;
バケット法では距離分だけ上記の演算をする(全米データ1対全では 4000万~5000万回ほど)ため、除算のコストがばかにならない。以下のように if 文に書き直すことで改善できる。
i++;
if (i >= bucket_size) i = 0;
また、bucket_size が2のべき乗であるならば、さらに改善できるようなので、bucket[] を切り上げて使用するというのも手のなのかもしれない。
アクセスパターン解析と並行して演算の再確認をしておこうと思う。












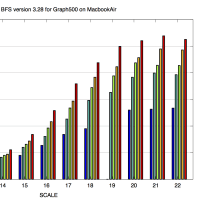
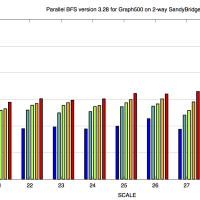
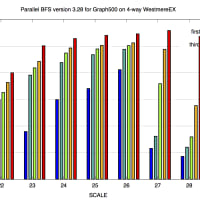
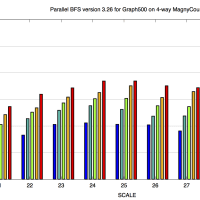
例のサイクルカウンタを使って計算時間全体に占める割合を算出するんですが、Intel 系列だと rdtsc のスループットが 64 サイクル程度と大きいので、Opteron を使うといいです(Penryn という手もあるがそれでもまだ大きい)。
あと、問題になるのが bucket_size の数値の大きさ。これが大きいと当然ながら遅くなります。^2 にするともちろん最高ですが、配列のアクセスに気をつけないとキャッシュコンフリクトが出ます。
もし、本当にこの部分がボトルネックになっているならば、Penryn 上での実行時間がかなり短くなっているはずです。Core2 との比から推定してみるのも良いです。
バケット法では枝長の分だけ、この循環リストのインクリメントを行うことになりますので、整数除算もボトルネックの一つになると思われます。
単純に実行時間の比較だけは次の記事で結果を載せておりますが、確かに penryn の方が高速化の割合が大きいです。
ちなみに bucket_size は全米では 368855 になります。このサイズは大きいと考えてよいのでしょうか。サイクルカウンタでも計測してみます。
整数除余算の問題点は、プロファイルやパフォーマンスカウンタでは検出できないのと、計算自体にやたらと時間を要するということです。
Alpha アーキテクチャみたいに整数除算命令を持っていないシステム上でプロファイルを採ると一発で問題点がわかるんですけどね。Intel 系は便利な命令がたくさん用意してあるので、このような場合には逆に苦労することになります。
1.データのロードの合間に余算を行う。余算に要する時間はデータのロードとそれほど大きな違いがないため、オーバーラップさせる。欠点はせいぜい倍しか速くならない。
2.テーブルを使って商を求めてから、乗算と引き算を使って余算を求める。10倍くらい速くなるが除数が大きいとテーブルが大きくなってしまい、テーブルのキャッシュミスで性能が落ちる。
3.余算用のベクトル演算ルーチンを作る。余算の演算で互いに依存性がある場合には使えないが、性能は50倍くらい速くなる。キャッシュに対する悪影響も少ない。Itanium2 では1要素あたり2サイクル以下の効率で計算が可能だったはず。
というわけで、お勧めは3です。1は完全にアーキテクチャ依存で、組み込み系のチップでは性能は出ないです。2はキャッシュの大きさに依存するのであまり良くないです。