3/16（日）認めません！！

昨日からくしゃみ鼻水です。
花粉症デビューだと妻や息子に言われていますが
断じて認めません！

とは言いつつ、とりあえず仕事部屋用に急きょ買ってきました。。

3/13（木）昨日の答え

昨日の問題の答えです。

秋山先生が解説していた方法で説明します。
この方法はまったく数学的な計算などは行いません。

＜問題＞
子供たち（A～Jくん）に体験してもらおうと、各スポーツクラブのコーチが集まりました。
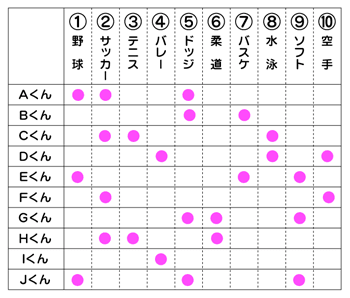
体験したいスポーツをまとめたのが下の表です。体験時間は各スポーツ1時間。
さて、効率よい時間割を考えましょう。


＜秋山先生の示した回答方法＞
（1）10種のスポーツを1～10の数字にして円形にならべます。
　　そして、同時に行えない数字同士を線でつなぎます。
　　例えば、Aくんは野球とサッカーとドッジの3つを希望してますが
　　同時にはできないのでその3つを線でつなぎます。


（2）同じようにBくん、Cくんの分の線を加えていきます。


（3）全員の線をひくとこうなりました。


（4）さあ、もう仕上げなんです。
　　各数字に色を付けていくんですが、1つルールがあります。
　　「線でつながった相手とは違う色にすること」

　　・「1」をピンクにします。
　　・「2」は「1」とつながっているので黄色にします。

　　・「3」は「2」とはつながってるけど
　　　「1」とはつながっていないのでピンクでOK。

（5）このルールに従ってこういう色分けができました。

　　　※結果には何パターンかあります。
　　　この色分けした数が必要な時間数になります。
　　　今回は5色使ったので5時間ということです。

（6）まったく計算をしないで効率の良い時間割を作ることができました。


数学的には、線と点で示されているので「グラフ」になるんだそうです。
JRや地下鉄の路線図、高速道路の案内なんかもそう。
複雑な情報を視覚的にわかりやすく表すことができるのが「グラフ」なんだということ。
たしかに。
この方法だと「野球とサッカー、バレーとバスケなど場所の都合で同時にできない」など、複雑な条件も追加できますし、なんたって、小3の息子レベルでもできそうじゃないですか。
素晴らしい！すごいぞ秋山先生！数学って面白い！
と、感動したところで、おしまい（笑）

3/12（水）問題です。

テレビでおもしろい問題があったのでここにメモ。
講師は秋山仁先生。
後で息子に教えてあげよう。

その問題とはこちら。（設定はちょっと変えています）

Q：子供たち（A～Jくん）に体験してもらおうと、各スポーツクラブのコーチが集まりました。
体験したいスポーツをまとめたのが下の表です。体験時間は各スポーツ1時間。
さて、効率よい割り振りを考えましょう。



答えは明日アップします（笑）

3/11（火）へくしっ！

なってみなければ本人の辛さはわからないんでしょうけど
息子を見ていると、やっぱり花粉症は大変だなと思います。。
去年はさほど症状が出なかったのに、今年は辛そう。
習い始めたがっている野球も、今しばらくは様子見かなあ。
今日みたいな日に洗濯物が外に干してある家を見ると、平和でうらやましい。
と、同時にそのうち来るぞぉ～。とも（笑）
ま、自分もいつデビューするかわかりませんけど。

3/10（月）6年間ありがとう。

息子が幼稚園に入園する時に
大好きだったアンパンマンの布で妻が手作りしたカバン。

小学3年も終わろうという今も、文句一つ言わずに学校へ持っていく息子。
ずいぶんボロボロになって、さすがに今学期で使い納めになりそうです。