階乗！から三角関数が顔をだす

　最近であった数学の話題です。

ご存じ階乗 2! =2,　3!=6, 4!= 24 　・・・となりますが、 n ! = (n-1)! × n の関係があります。　ではこの n を有理数・実数などに拡張し、　1.5 ! の計算はできないものでしょうか？

　この計算を行うのが、Γ（ガンマ）関数。平たくいうと、自然数のみだった「階乗」を拡張したものです。　Γ(1) ,Γ(2),Γ(3) ・・・が階乗に相当するのですのですが、正しくは Γ(n+1) = n! となります。　

　階乗を拡張したΓ関数ですが、　別の計算をすると、三角関数が表れます。その式は

　Γ(x)Γ(1－x)=π/sin(πx)　というシンプルなものです。

　ζ（ゼータ）関数というのも、興味をそそり、

 1+2+3+4+5 ・・・ =∞ではなく、 = - 1/12 となるのです。下記の書籍での出会い。

（参考）　へんな数式美術館 ~世界を表すミョーな数式の数々~ (知りたい!サイエンス)

　　　　　https://ja.wikipedia.org/wiki/1%2B2%2B3%2B4%2B…

---

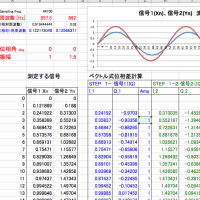
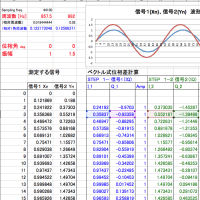
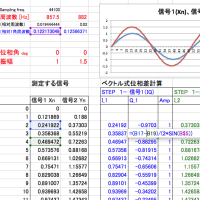
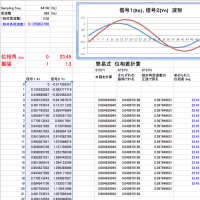
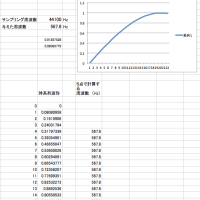
 今取り組もうとしているのは、「多重三角関数」。私の研究成果である、Synchro PRIMO法を複数成分に拡張しようとすると三角関数の展開は超難解。また、自身の提案した方法の「一般化」もめざして「パルス」の位相差にも取り組んでいるところ。

　数学のネタを探していたら、Γだのζなど、読めない関数にであい。引き込まれてしまいました。　大学２年で「複素解析」をやっていれば、入門としてはついていけると思います。