1.2.1 期待順位値の導入
麻雀は選択の連続です。
「どの牌を切るか?」
「鳴くか、鳴かないか?」
「リーチか、ダマか?」 etc
そして、より優れていると思った選択肢を
我々は選んでいくわけです。
では、「より優れている選択肢」とはどういうことでしょうか?
それは、
「ゲーム終了時に良い順位であるために最良な選択肢」
と言い換えられます。
つまり、麻雀における最良の選択肢を判断するには
ある選択肢を選んだと仮定した場合に
最終的な順位がどれくらいになるかを、
全ての選択肢について正しく把握しなければいけません。
この「最終的な順位がどれくらいになるか」を表す値を
期待順位値と呼ぶことにします。
期待順位値は以下のように定義できます。
期待順位値
=(1×1位を取る確率)+(2×2位を取る確率)+(3×3位を取る確率)+(4×4位を取る確率) 式(1.2.1.)
例えば、ゲーム開始直後で配牌を見る直前は
1位をとる確率も2位を取る確率も3位を取る確率も4位を取る確率も
全て等しく25%なので(厳密には違いますが、ここでは考慮せず。)
期待順位値は
1×0.25+2×0.25+3×0.25+4×0.25=2.5 式(1.2.2)
よって、期待順位値 2.50位
となります。
ここで、東一局で8000点をあがったとすると、
1位や2位を取る確率が上がり、3位や4位を取る確率は下がるので
期待順位値は2.50位より良くなります。
反対に東一局で8000点を振り込むと、
1位や2位を取る確率が下がり、3位や4位を取る確率は上がるので
期待順位値は2.50位より悪くなります
1.2.2 期待順位値と他家との点数差
では、点棒移動が生じると期待順位値は
具体的にどのように変化するのでしょうか?
図1.2.1は、自分とある一人の他家との点差と
期待順位値の変化量の関係を表したグラフです。[1]
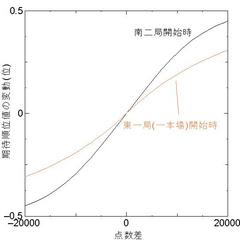
図1.2.1 ある一人の他家との点差と期待順位値の変化量の関係[1]
(他の局のグラフを知りたければ、
引用元の「科学する麻雀」(講談社)をご覧下さい。)
例えば、東一局一本場開始時に
ある一人の他家に16000点差をつけていると、
期待順位値は2.50位から0.25位ほど良くなります。
同様に、他の二人の他家にも16000点差をつけているとしましょう。
(これは開局で4000オールをあがった場合に相当)
そうすると、他の他家に対してもそれぞれ0.25位ほど有利になるので
他家三人合計で、
0.25×3=0.75位分の期待順位が良くなります。
1.2.3 平場の定義と期待値
さて、ここでもう一度図1.2.1をご覧下さい。
東一局なら±20000点くらいまで
南二局なら±10000点くらいまでは、
他家一人との点差と期待順位値の変化量は
比例しているといえます。
つまり、局にもよりますが
点差が競っているときは、
他家との点差がそのまま期待順位値の変化を示す
ということができます。
これが点差が開いてしまっている状況、
例えば、南二局で18000点差の場合
大きくあがっても期待順位値はあまり向上しないことが
グラフから読み取れます。
今回、押し引きを論じるにあたっては
点差が競っていて、点差がそのまま期待順位値の
変化量を表す場合について考えていきます。
また、他家三人の点差と期待順位値の変化量が比例している状況を
平場と呼ぶことにします。
さて、平場においては他家三人との点差の合計が
そのまま2.50位からの期待順位値の変化になるのですが、
麻雀は四人の点数の合計が常に一定であることから
他家三人との点差の合計が決定されると
一意的に自分の持ち点が決まります。
簡単なことですが、一応証明しておきます。
∵
原点をX点とする。つまり、4人の点数の合計は4X点。
ある任意の局の他家三人にリードしている分の点数差を
それぞれa点、b点、c点とおき
自分の持ち点をY点とおくと、
4人の合計点数は 4Y-(a+b+c)点。
今、4X=4Y-(a+b+c)より
Y=X+(1/4)(a+b+c)
ゆえに、三人との点数差の合計a+b+cが決定されると
自分の持ち点Y点が決まる。 //
よって、平場においては
「自分の持ち点の変化が
そのまま期待順位値の変化につながる」
といえます。
ここから、平場での押すか引くかの判断はそれぞれの場合で
どの程度の持ち点の変化が見込まれるか
すなわち、それぞれの期待値を計算し
期待値が高い方を選択すればよいわけです。
参照
[1]とつげき東北 「科学する麻雀」 講談社 2004年
前へ 次へ 目次へ
麻雀は選択の連続です。
「どの牌を切るか?」
「鳴くか、鳴かないか?」
「リーチか、ダマか?」 etc
そして、より優れていると思った選択肢を
我々は選んでいくわけです。
では、「より優れている選択肢」とはどういうことでしょうか?
それは、
「ゲーム終了時に良い順位であるために最良な選択肢」
と言い換えられます。
つまり、麻雀における最良の選択肢を判断するには
ある選択肢を選んだと仮定した場合に
最終的な順位がどれくらいになるかを、
全ての選択肢について正しく把握しなければいけません。
この「最終的な順位がどれくらいになるか」を表す値を
期待順位値と呼ぶことにします。
期待順位値は以下のように定義できます。
期待順位値
=(1×1位を取る確率)+(2×2位を取る確率)+(3×3位を取る確率)+(4×4位を取る確率) 式(1.2.1.)
例えば、ゲーム開始直後で配牌を見る直前は
1位をとる確率も2位を取る確率も3位を取る確率も4位を取る確率も
全て等しく25%なので(厳密には違いますが、ここでは考慮せず。)
期待順位値は
1×0.25+2×0.25+3×0.25+4×0.25=2.5 式(1.2.2)
よって、期待順位値 2.50位
となります。
ここで、東一局で8000点をあがったとすると、
1位や2位を取る確率が上がり、3位や4位を取る確率は下がるので
期待順位値は2.50位より良くなります。
反対に東一局で8000点を振り込むと、
1位や2位を取る確率が下がり、3位や4位を取る確率は上がるので
期待順位値は2.50位より悪くなります
1.2.2 期待順位値と他家との点数差
では、点棒移動が生じると期待順位値は
具体的にどのように変化するのでしょうか?
図1.2.1は、自分とある一人の他家との点差と
期待順位値の変化量の関係を表したグラフです。[1]

図1.2.1 ある一人の他家との点差と期待順位値の変化量の関係[1]
(他の局のグラフを知りたければ、
引用元の「科学する麻雀」(講談社)をご覧下さい。)
例えば、東一局一本場開始時に
ある一人の他家に16000点差をつけていると、
期待順位値は2.50位から0.25位ほど良くなります。
同様に、他の二人の他家にも16000点差をつけているとしましょう。
(これは開局で4000オールをあがった場合に相当)
そうすると、他の他家に対してもそれぞれ0.25位ほど有利になるので
他家三人合計で、
0.25×3=0.75位分の期待順位が良くなります。
1.2.3 平場の定義と期待値
さて、ここでもう一度図1.2.1をご覧下さい。
東一局なら±20000点くらいまで
南二局なら±10000点くらいまでは、
他家一人との点差と期待順位値の変化量は
比例しているといえます。
つまり、局にもよりますが
点差が競っているときは、
他家との点差がそのまま期待順位値の変化を示す
ということができます。
これが点差が開いてしまっている状況、
例えば、南二局で18000点差の場合
大きくあがっても期待順位値はあまり向上しないことが
グラフから読み取れます。
今回、押し引きを論じるにあたっては
点差が競っていて、点差がそのまま期待順位値の
変化量を表す場合について考えていきます。
また、他家三人の点差と期待順位値の変化量が比例している状況を
平場と呼ぶことにします。
さて、平場においては他家三人との点差の合計が
そのまま2.50位からの期待順位値の変化になるのですが、
麻雀は四人の点数の合計が常に一定であることから
他家三人との点差の合計が決定されると
一意的に自分の持ち点が決まります。
簡単なことですが、一応証明しておきます。
∵
原点をX点とする。つまり、4人の点数の合計は4X点。
ある任意の局の他家三人にリードしている分の点数差を
それぞれa点、b点、c点とおき
自分の持ち点をY点とおくと、
4人の合計点数は 4Y-(a+b+c)点。
今、4X=4Y-(a+b+c)より
Y=X+(1/4)(a+b+c)
ゆえに、三人との点数差の合計a+b+cが決定されると
自分の持ち点Y点が決まる。 //
よって、平場においては
「自分の持ち点の変化が
そのまま期待順位値の変化につながる」
といえます。
ここから、平場での押すか引くかの判断はそれぞれの場合で
どの程度の持ち点の変化が見込まれるか
すなわち、それぞれの期待値を計算し
期待値が高い方を選択すればよいわけです。
参照
[1]とつげき東北 「科学する麻雀」 講談社 2004年
前へ 次へ 目次へ



















暖かい一日、どのように過ごしましたか?
またブログで教えてくださいね。
楽しみに待ってます。
今日は風が強いですね~
春一番がふくかも?!
ブログ待ってますね!
今日は寒くなるそうですね。
体調管理には気をつけてくださいね。
応援してます。
楽しみにしています。