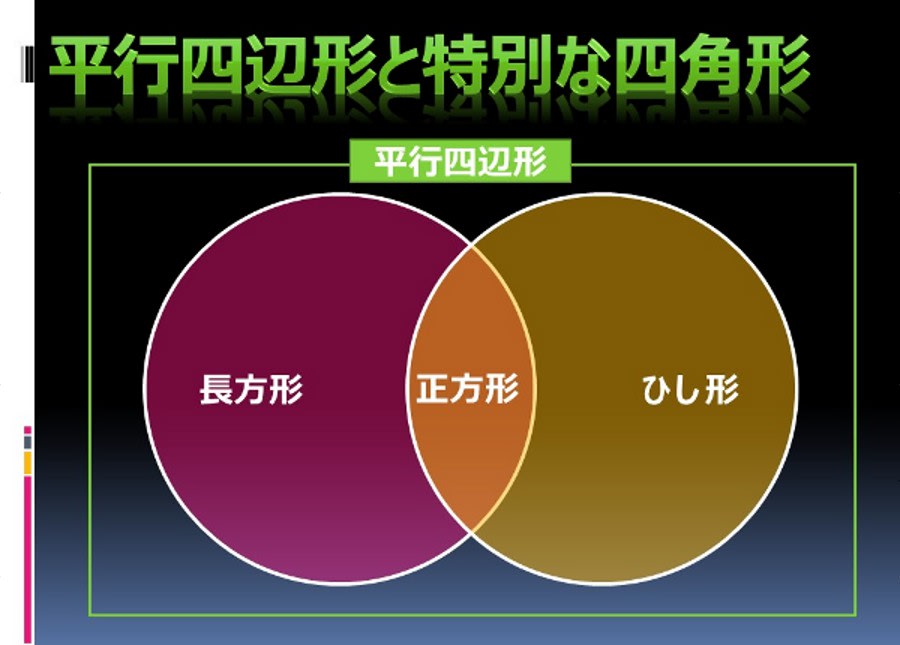
高校入試と「平行四辺形の定義と定理について」

高校入試と「平行四辺形の定義と定理について」




図形の「定理」は定義と違い複数存在するので、証明の方法も１通りとは限りません。

辺の長さだけでなく角度などを使った証明も可能になるので、「定義」と「定理」をすべて覚えて、

どの条件を証明に用いるべきかを判断できるようにしましょう。


◎ 平行四辺形： 2組の向かい合う辺がそれぞれ平行な四角形 （定　義）

　定　理1： 「平行四辺形の2組の向かい合う辺はそれぞれ等しい」

　〈証　明〉

　　　平行四辺形のACを結ぶ対角線を引きます

　　　

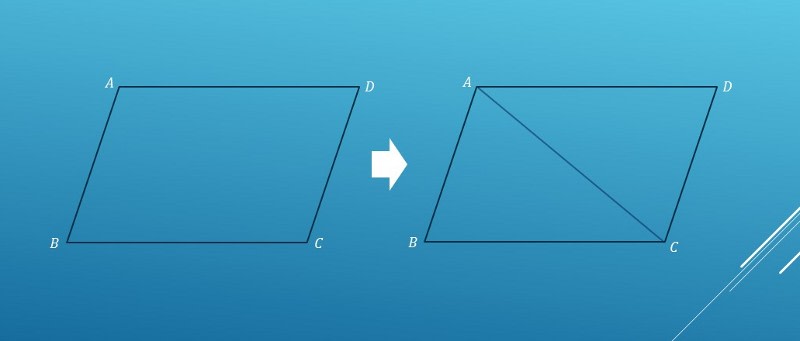
　　　△ABC と△CDA において、
　　　∠BAC＝∠DCA，∠BCA＝∠DAC　――　①　（平行線の錯角）
　　　AC＝CA　――　②　（共通の辺）

　　　①②より、　1辺とその両端の角がそれぞれ等しい2つの三角形は合同　であるから、
　　　△ABC ≡ △CDA 　である

　　　合同な図形の対応する辺の長さはすべて等しいので、
　　　AB＝CD, AD＝CB　である　・・・　証明終わり


　定　理2： 「平行四辺形の2組の向かい合う角はそれぞれ等しい」

　〈証　明〉

　　　定理1．のと同様に、補助線としての対角線ACを引き、△ABC≡△CDAであることを証明してから、

　　　合同な図形の対応する角度はすべて等しいので、
　　　∠ABC＝∠CDA，　∠BAC＝∠DCA，　∠BCA＝∠DAC
　　　∠BAD＝∠BAC＋∠DAC，　∠BCD＝∠BCA＋∠DAC　であるから、
　　　∠BAD＝∠BCD　・・・　証明終わり


　定　理3： 平行四辺形の対角線はそれぞれの中点で交わる

　〈証　明〉

　　　平行四辺形のAC, BD を結ぶ2本の対角線を引きます。

      

　　　△ABO と △CDO において、
　　　∠OCD＝∠OAB， ∠OBA＝∠ODC　――　①　（平行線の錯角）
　　　AB＝CD　――　②　（平行四辺形の対辺）

　　　①②より、　1辺とその両端の角がそれぞれ等しい2つの三角形は合同であるから、
　　　△ABO ≡ △CDO　である。

　　　合同な2つの図形の対応する辺の長さはすべて等しいので、
　　　OB＝OD，OA＝OC　・・・　証明終わり


次に、この3つの定理の逆　「○○ならば平行四辺形である」　について復習します。


　定理1の逆： 「向かい合う2組の辺がそれぞれ等しい四角形は平行四辺形である」

　　　定理1同様、補助線ACを引けば、

　　　

　　　仮定より、AB＝CD，AD＝BC　――　①
　　　　　　　 　　　AC＝CA　――　②　（共通の辺）

　　　合同条件 「3辺がそれぞれ等しい」より、　△ABC ≡ △CDA

　　　合同な図形の対応する角はすべて等しいので、
　　　　　　∠BAC＝∠DCA　――　③　
　　　　　　　∠BCA＝∠DAC　――　④

　　　③④より、　錯角が等しい2つの直線は平行であるから、
　　　　　　AB // DC，　AD // BC

　　　よって、　

　　　向かい合う2組の辺が平行であるからこの四角形は平行四辺形である　・・・　証明終わり


　定理2の逆： 「向かい合う2組の角がそれぞれ等しい四角形は平行四辺形である」

　〈証　明〉

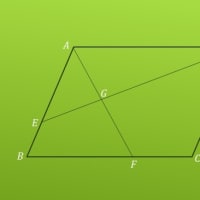
　　　平行四辺形ABCDのABの延長線BEを引きます

　　　

　　　仮定より、∠A＝∠C，∠B＝∠D　――　①
　　　　　　　∠A＝∠C＝x， ∠B＝∠D＝y  とすると
　　　　　　　　∠A＋∠B＋∠C＋∠D＝360°　より
　　　　　　　　　　x＋y＋x＋y ＝360°　　2（x＋y）＝360°
　　　∴　 x＋y＝180°　――　③

　　　直線のつくる角は180°であるから、
　　　　　　　　　∠B＋∠CBE＝180°   　y ＋∠CBE＝180°
　　　③より、　∠CBE＝x 　――　④

　　　これにより、　∠A＝∠C＝∠CBE＝x   ――　⑤
　　　このとき、∠Aと∠CBEは同位角、∠Cと∠CBEは錯角に当たるので、

　　　⑤より、　AD // BC，  AB // DC

　　　よって、

　　　向かい合う2組の辺が平行であるからこの四角形は平行四辺形である　・・・　証明終わり


　定理3の逆： 「四角形の対角線がそれぞれの中点で交わるならば、この四角形は平行四辺形である」

　　　四角形ABCDのAC, DB を結ぶ対角線の交点をOとするとき、

　　　

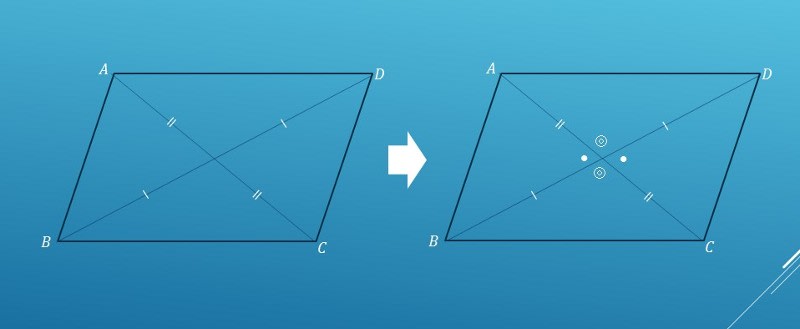
　　　△ABOと△CDOにおいて、
　　　仮定より、AO＝CO，BO＝DO　――　①
　　　　　　　　　∠AOB＝∠COD　――　②　（対頂角）

　　　①②より、2辺とその間の角がそれぞれ等しい2つの三角形は合同 であるから、
　　　△ABO ≡ △CDO　である。

　　　合同な図形の対応する角はすべて等しいので、
　　　∠BAO＝∠DCO であり、錯角が等しいので　AB // DC　――　③

　　　同様に、△BCOと△DAOにおいて、
　　　仮定より、AO＝CO，BO＝DO　――　①
　　　　　　　　　∠AOD＝∠COB　――　②　（対頂角）

　　　①②より、2辺とその間の角がそれぞれ等しい2つの三角形は合同であるから、
　　　△BCO ≡ △DAO　である。

　　　合同な図形の対応する角はすべて等しいので、
　　　∠OCB＝∠OAD であり、錯角が等しいので　AD // BC　――　④

　　　③④より、向かい合う2組の辺が平行であるからこの四角形は平行四辺形である　・・・　証明終わり



〈演習問題にチャレンジ〉

　　　　　　　　　「四角形ABCDにおいて、AD＝BC, AD // BC であるならば、この四角形は平行四辺形で
　　　　　　　　　あることを証明しなさい」

　　　　　　　　　　




〈前回の演習問題の答え〉


　　　　　

授業で学習した内容をしっかり身に着ける！
☆　[要点整理]と[演習問題]を一体化した実践学習 〉〉

　*　桜華塾の［英語・数学］対応講座