高校入試と「合同の証明」

高校入試と「合同の証明」




数学において「合同」は、

　　　　　　　「2つの図形の一方を移動して他方に重ねたとき、ぴったりと重なり合う状態」

をいいます。

三角形については、わざわざ重ね合わせなくても「合同」であると判断する手段があり、

「三角形の合同条件」　に当てはめることになります。

上の図のように、三角形の合同条件は3つ

　　　　　　　　1）　3辺の長さがそれぞれ等しい

　　　　　　　　2）　2辺の長さとその間の角度がそれぞれ等しい

　　　　　　　　3）　1辺の長さとその両端の角度がそれぞれ等しい


〈合同の証明〉

　「証明」するとは、仮定や図形の性質などを根拠に与えられた命題が正しいと

結論づける　ことをいいます。

　　　　「仮定」は、あらかじめ与えられている「決まりごと」　のことで、

　　　　「結論」は与えられた命題が正しい事柄であると導き出すこと。

証明するとき、　「○○という理由から、××である」　という形の文章表現をしますが、

「〇〇」に当たる部分が仮定や図形の性質を表し、

「××」に当たる部分が結論（2つの三角形は合同である）になります。


〈証明の手順〉

「2つの三角形は合同である」　と結論づける文を完成させる手順をしっかり覚えてください。

　　　　　　　手 順 1．証明の対象を明らかにする
　　　　　　　　　　　　　　　　　　→　どの図形とどの図形についての証明か

　　　　　　　手 順 2．証明の対象について、仮定や図形の性質を述べる

　　　　　　　手 順 3．3つの合同条件のどれを用いるか明らかにする
　　　　　　　　　　　　　　　　　→　「手順2 から〇〇の合同条件が成り立つ」　という説明

　　　　　　　手 順 4．結論づける


〈合同を利用する問題〉

入試問題では、「2つの三角形が合同であるから△△が成り立つ」という別の性質を導き出させるものが

よく出題されます。主に、角度や線分の長さに関するものになり、

　　　　　　　「合同な図形の対応する辺や角は等しいから△△である」　

という文章を作成します。


・入試問題にチャレンジ：

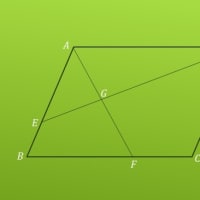
　　　　　　　「図において、四角形ABCDは正方形であり、△CEFはCE＝CF の直角二等辺三角形である。
　　　　　　　このとき、△BCF≡△DCE であることを証明しなさい」

　　　　　　　　

　受験勉強は「マラソン競技」と同じ！　
スタートダッシュで先頭集団をキープできたら自分のペースを
守りゴールを目指して少しずつ確実に前進しよう！

☆　独自の学習法で知識の使い方が学べる学習講座！ 〉〉

　*　桜華塾の［英語・数学］対応講座