引き続き、割り算の文章題です。
例題②
90を□で割ると6余り、136を□で割ると10余ります。
(ただし、□は、考えられる整数のうちで、いちばん小さい数とします。)
前回の例題①と同様に「割る数」を出す問題ですが
例題①とは違い、余っている数が同じではありませんね。
しかし、考え方は同じです。
90を割ると6余る、ということは、6少なければ割り切れる
136を割ると10余る、ということは10少なければ割り切れる
ということですね。
90−6=84
136−10=126
84と126を割り切れる数=84と126の公約数ですね!
公約数=最大公約数の約数ですので、早速すだれ算で出していきましょう!
84と126を並べて書いて

どちらも一の位が偶数ですので、2で割りましょう。

84÷2=42
126÷2=63 ですのでこうなりますね。

まだ割れそうですね。
今度は片方の一の位は偶数ではないので、2はダメですね。
しかし、両方とも7の段にありますねえ。
ということで7で割りましょう。
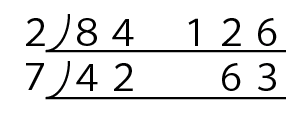
こんな風に下に書いていきます。
42÷7=6
63÷7=9 ですのでこうなりますね。

6と9ですので3で割れますね。
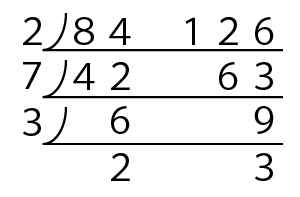
こうなります。
もう割れないので、すだれ算はここで終了です。
最大公約数は、すだれ算の
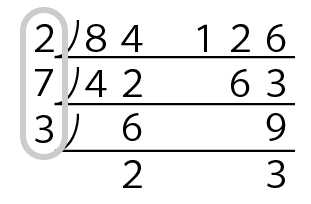
ここの部分をかけたものになります。
2×7×3=42
が84と126の最大公約数ですね!
ここで問いに戻ると、余りが6と10ですので、
割る数は10より大きくないといけません。
10より小さい数、例えば5とかで割れば、10の中にまだ5はありますから、10余ることはないのですね。
(前回、ここの部分をすっとばして答えを出してしまいました‥追記しておきました。申し訳ありません)
ということで、求める数は42の約数のうち10より大きい数です。
約数は最大公約数を小さい数から割っていって出します。
その数を割れる一番小さい数は1なので、まず1を書き、
その下に1で割った答えを書きます。

こんな感じですね。
1の次に割れる数を、1の横に書き、その下に割った答えを書きます。

2で割れるので、こうなりますね。
同じように、順に割れる数で割って答えを書いていきます。

6の次は7で割れますが、7はもう書いてあるのでここで終了です。
42の約数は 1、2、3、6、7、14、21、42 と分かりました!
この中で10より大きい数は 14、21、42
この中でいちばん小さい数は14
ということで答えは 14
どうでしょうか?
余っているということはどういうことか?が理解出来れば簡単ですね!
すだれ算、約数の出し方などもスムーズにできるようにしておきましょう!
次回は例題③です!
例題②
90を□で割ると6余り、136を□で割ると10余ります。
(ただし、□は、考えられる整数のうちで、いちばん小さい数とします。)
前回の例題①と同様に「割る数」を出す問題ですが
例題①とは違い、余っている数が同じではありませんね。
しかし、考え方は同じです。
90を割ると6余る、ということは、6少なければ割り切れる
136を割ると10余る、ということは10少なければ割り切れる
ということですね。
90−6=84
136−10=126
84と126を割り切れる数=84と126の公約数ですね!
公約数=最大公約数の約数ですので、早速すだれ算で出していきましょう!
84と126を並べて書いて

どちらも一の位が偶数ですので、2で割りましょう。

84÷2=42
126÷2=63 ですのでこうなりますね。

まだ割れそうですね。
今度は片方の一の位は偶数ではないので、2はダメですね。
しかし、両方とも7の段にありますねえ。
ということで7で割りましょう。
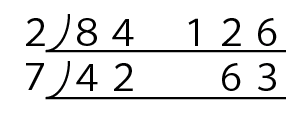
こんな風に下に書いていきます。
42÷7=6
63÷7=9 ですのでこうなりますね。

6と9ですので3で割れますね。
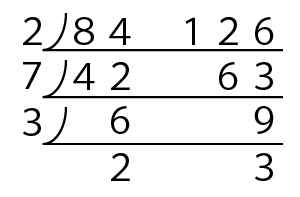
こうなります。
もう割れないので、すだれ算はここで終了です。
最大公約数は、すだれ算の
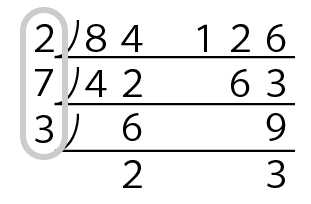
ここの部分をかけたものになります。
2×7×3=42
が84と126の最大公約数ですね!
ここで問いに戻ると、余りが6と10ですので、
割る数は10より大きくないといけません。
10より小さい数、例えば5とかで割れば、10の中にまだ5はありますから、10余ることはないのですね。
(前回、ここの部分をすっとばして答えを出してしまいました‥追記しておきました。申し訳ありません)
ということで、求める数は42の約数のうち10より大きい数です。
約数は最大公約数を小さい数から割っていって出します。
その数を割れる一番小さい数は1なので、まず1を書き、
その下に1で割った答えを書きます。

こんな感じですね。
1の次に割れる数を、1の横に書き、その下に割った答えを書きます。

2で割れるので、こうなりますね。
同じように、順に割れる数で割って答えを書いていきます。

6の次は7で割れますが、7はもう書いてあるのでここで終了です。
42の約数は 1、2、3、6、7、14、21、42 と分かりました!
この中で10より大きい数は 14、21、42
この中でいちばん小さい数は14
ということで答えは 14
どうでしょうか?
余っているということはどういうことか?が理解出来れば簡単ですね!
すだれ算、約数の出し方などもスムーズにできるようにしておきましょう!
次回は例題③です!










※コメント投稿者のブログIDはブログ作成者のみに通知されます