三角関数の変な公式？

　必要あって、次の計算式に取り組んでいました。

cos^2(θ) - cos^2(2θ) = sinθ・sin3θ　

cos^2(0) - cos^2(θ) =  sinθ・sinθ　（単純には 1-cos^2(θ)=sin^2(θ))

これを一般化して、

cos^2(nθ) - cos^2{(n+1)θ} = sin θ・sin (2n+1)θ　　を、とりあえず証明しました。

 

実は以前に説明した「リサージュ外積」 Lsをz領域で表したとき遅延段数kを1,2,3....としたときの一般形を知りたかったのです。 

展開と導出はそれほど難しくはなく、与式をまず「和差の積」に変換、次に三角関数の「和積変換」、sin cos の項に集めると「倍角の公式」を用いてさらに簡単になり目的の式ができあがりです。

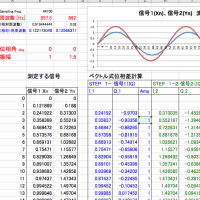
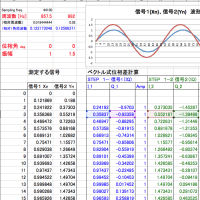
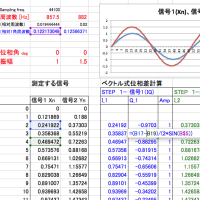
　当社の周波数測定方法（計算方法）は、「リサージュ外積比(=r)」を解いて、目的の周波数を計算しているのですが、現在までにわかっている計算式は、1) r=Ls2/Ls1 とする「倍角法」、2)r=Ls3/Ls1 とする「三倍角法」　だけです。 

r = Ls5/ Ls3 のような形ではどうなるか・・・

結局、上の・・・"余弦自乗差・正弦倍角変換？　をつかうと、 r = sin(mΩ) / sin(nΩ)　という式で、与えたm,nの条件下で求めたい周波数Ωを解くことになるのです。　他に３つ以上のリサージュ外積を組み合わせた解法も（数学的には）可能ででしょうが、どんな性質や性能となるかは予想がついておりません。狙いとしては, Ls1,Ls2,Ls3 ....と適当なところまで使用した計算式。複数を組み合わせることでお得な何かがあればいいかと思っています。