アサルトアーマーRevenge/Part2

Part1レギュ1.30でのAA攻撃力計算に先立ち
Part216000≦PAのAA攻撃力式
Part312000≦PA≦16000のAA攻撃力式
Part49000≦PA≦12000のAA攻撃力式
Part5PA≦9000のAA攻撃力式
Part6AA攻撃力計算式まとめ
Part7PA満タン以外でも計算式を成立させる


Part2はPA≧16000についてです。

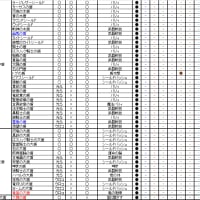
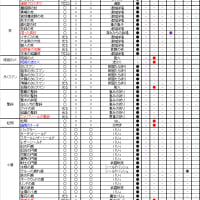
計算式導出に用いる総合AA攻撃力の実測値は、


総合AA攻撃力から算出したAA攻撃力は、


各AA攻撃力/OBについて、段数を変数とした近似直線の傾きと切片は、


傾きについて、値の傾向を見ると、


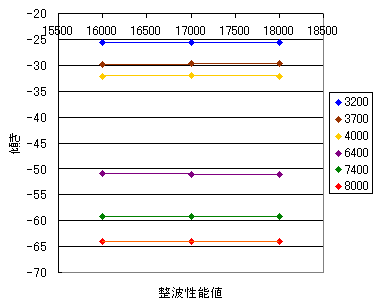
傾きはPA値が変化しても同値をとっていると判断出来る。そこで任意のPA値として、PA16000について、AA攻撃力/OBを変数として傾きを見ると以下のようになる(PA17000やPA18000はPA16000のグラフと被るため割愛)。

傾き-傾きはPA17000では-0.007999、PA18000では-0.007990である。傾き-切片は、PA17000では0.03267、PA18000では-0.054155である。これらが同値であるという仮定から、傾き-傾きは-0.008であり、傾き-切片は0に補正されると考えられる。今後のPA範囲でも同様のことであるが、補正することによる計算値への影響は最後に確認する。妥当かそうでないかは最終結果で分かります。


切片は、

切片-傾きは0.3080程度である。

ここで(傾き-傾き)＋(切片-傾き)＝0.30になることが分かる。切片-切片は、

0.12×PAと読み取れる。なお、切片-切片近似式の切片は0に補正している。


以上から、
PA≧16000において、段数をZ、AA攻撃力/OBをAAとおくと、

AA攻撃力
＝-0.008×AA×Z＋0.3080×AA＋0.12×PA
＝{(Z-1)(-0.008)＋0.30}×AA＋0.12×PA

ここで、PA19522(P-MARROW装備可能な最大PA)とPA20282(最大PA)の総合AA攻撃力の実測値を示す。


総合AA攻撃力から求めたAA攻撃力は、


となる。

そして、PA≧16000でのAA攻撃力の計算値を示す。


計算値-実測値の差をとって求めた平均絶対誤差は0.39521、最大絶対誤差は1.19564であり、EN防御最低機体(EN防御3828)のAP1に相当する攻撃力1.41736よりも小さいため、十分な精度の計算式であることが分かる。


改めて、
AA攻撃力＝{(Z-1)(-0.008)＋0.30}×AA＋0.12×PA (PA≧16000)

なお、総合AA攻撃力の式はAA攻撃力式から容易に組めるが、それはまとめのところで述べる。

Part3 12000≦PA≦16000のAA攻撃力式