折り紙で大二十・十二面体（Great Icosidodecahedron）～素晴らしい星型多面体

折り紙、新聞紙、チラシ、空き箱などで多面体を作って（編んだり、組みたてたりして）います。

今回は、折り紙で大二十・十二面体（Great Icosidodecahedron）を作って（組みたてて）みました。

※今までに折り紙で作った（編んだり、組みたてたりした）多面体
　○菱形十二面体の星型
　○菱形三十面体
　○菱形六十面体

　○小星型十二面体(Small stellated dodecahedron)と大星型十二面体(Great stellated dodecahedron)

　○3つの正八面体の複合多面体（Compound of three Octahedra）
　○5つの正八面体の複合多面体（我が家での呼び方は「美しすぎる120面体」）

　○5つの正四面体の複合多面体（Compound of five tetrahedra）Part1
　○5つの正四面体の複合多面体（Compound of five tetrahedra）Part2
　○5つの正四面体の複合多面体（Compound of five tetrahedra）Part3
　○6つの正四面体の複合多面体（Compound of six tetrahedra）Part1
　○6つの正四面体の複合多面体（Compound of six tetrahedra）Part2
　○10個の正四面体の複合多面体（Compound of ten tetrahedra）Part1
　○10個の正四面体の複合多面体（Compound of ten tetrahedra）Part2
　○大二十面体（The great icosahedron）Part1
　○大二十面体（The great icosahedron）Part2
　○2つの立方体の複合多面体（Compound of Two Cubes）
　○6つの立方体の複合多面体（Compound of six Cubes）

　○6五角形プリズムの複合多面体(Compound of 6 pentagonal prisms)

大二十・十二面体（Great Icosidodecahedron）は、3種類の図形（正五角形、凧型、菱形の一角を切り取った五角形）で組み立てることができます。

ＨＰ上に公開されている型紙を活用して無地のチラシで組みたて、五芒星12個、正三角形20個がわかるように9色で色塗りをしてみます。


この大二十・十二面体（Great Icosidodecahedron）を作る際の大きさの目安として、構成面の正三角形一辺の長さから星型を構成する3つの図形（正五角形、凧型、菱形の一角を切り取った五角形）の各辺の長さの関係をエクセルで表計算してみました。

※大二十・十二面体（Great Icosidodecahedron）の星型を構成する3つの図形の各辺の長さ、型紙等の計算には、ウィキペディア等ＨＰ上に数多く公開されている計算式を使わせていただきました。




型紙は、菱形の一角を切り取った五角形用…60個、正五角形用…12個、凧型用…60個、合わせて3種類132個です。


そして、折り紙は菱形の一角を切り取った五角形用の型紙60個は5色、正五角形用の型紙12個と凧型用の型紙60個は4色を用意します。

15㎝×15㎝の折り紙を使います。
菱形の一角を切り取った五角形用の型紙…5色の折り紙を重ねて型紙で切り取ります。

正五角形用の型紙12個と凧型用の型紙60個の型紙…4色の折り紙を重ねて型紙で切り取ります。

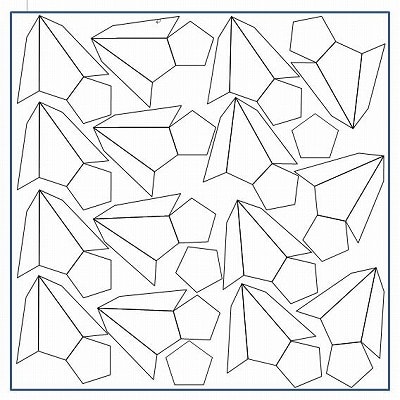
組み合わせ方


組み合わせていきます。



もう少しです。


素晴らしい星型多面体の完成です。


この大二十・十二面体（Great Icosidodecahedron）、均整がとれた可愛い星型の多面体で、見ているだけで心がうきうきしてきます。
ちょっと欲張って色々な方向からみた画像を載せてみました。













五芒星12個、正三角形20個、確認できますか？