まずは大問1の計算。基本が出来てなきゃ応用なんて出来ません
そして関数の基本へ、前回は式に数字を代入だけで取れる問題です
続きです。前回はこちら
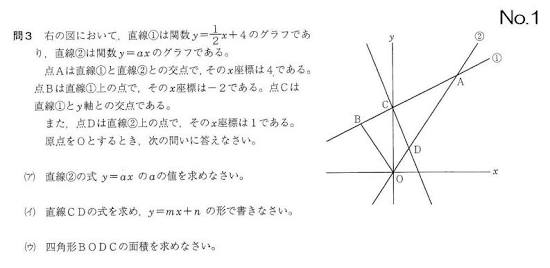
一つ目の画像は前回と同じ入試問題。共通テストに必ず出る一次関数と比例です
まず問題文にそって、数字や文字そして式をグラフ上に書き込んでいきます。数学は、文章で読むより数式やグラフのほうが圧倒的にカンタン。グラフに書き込んでおけば速く解けます。他の問題や見直しに時間が使えますよ
問題文を読みながら、グラフに書き込んでしまいましょう★
[関数の基本](↓自信がなきゃまた書け!忘れたらまた書け!!)
x軸とy軸のグラフでは、ひとつの点をx座標とy座標ふたつの座標(x,y)で表します
直線のグラフは一次関数★です
y=ax+b 、aは傾(かたむ)き 、bは切片(せっぺん)
原点(0,0)を通る直線のグラフは比例★です
y=ax 、aは傾(かたむ)き 、原点でy=0なのでbもゼロです
直線(1)や直線CDは一次関数。y=ax+bの形をとります
直線(2)や直線BOは原点を通る直線なので比例。y=axの形をとります
ここで使うxやyは変わる数、変数です
ここで使ったaやbには定まった数、定数が入ります
ここからが本題
[解説]
関数は仕事で使います。たとえば、あるひとの身長と体重の関(かか)わりのグラフ。この関わりは公式に出来ませんがグラフは描ける。たくさんのデータがあれば傾向も見えてきます。売れ筋商品の傾向、エンジンの効率、クスリの効果的な量、わたしたちの役に立つ傾向が見えてきます。グラフである範囲の面積を求めれば、散らばりぐあいを比べることが出来ます
それから面積の公式は覚えてますね?これは覚えておかないと、これからも解けるようにはなりません。一目で小学校の基本ですから。覚えてなきゃ書いて覚えてください。覚えるまで何度も写せばいい。学校の受験用教材にまとめてありますよ。
(ウ)四角形BODCの面積を求めなさい。
四角形BODCをグラフ上をなぞって確認します。わたしは薄い斜線で求める面がひと目でわかるようにしておきます。グラフの四角形に直角がありませんね。このままじゃ底辺と高さがわからない
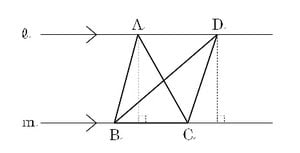
二つ目の画像(l∥m)を見てください。面積を求めるには、底辺と高さ以外は使いません。底辺と高さは直角に交(まじ)わります。関数のグラフでx座標とy座標は直角に交わりますね。これ使えるじゃん
まず底辺を定(さだ)めましょう。グラフの四角形BODCだけ見ます。ひとつの四角形と考えると直角は見えてきません。ふたつの三角形に分けたらどうでしょう。y軸でふたつに分けてみます
y軸のCOが底辺だとすると、右側の三角形DCOでは点Dからy軸までの距離が高さに、左側の三角形BCOでは点Bからy軸までの距離が高さになります。
〇三角形DCOの面積=CO×点Dのx座標×1/2
×三角形BCOの面積=CO×点Bのx座標×1/2
ただし!点Bのx座標はマイナスですからそのまま使えば面積もマイナスになってしまいます。|絶対値|を使って符号のない距離として扱えばいいんです
〇三角形BCOの面積=CO×|点Bのx座標|×1/2
点C(0,4)と原点O(0,0)より、COはたて軸ですからy座標のみ比べます。CO=4-0=4
また(ア)(ィ)までで求めた点D(1,3/2)を使います
三角形DCOの面積=4×1×1/2=2
「点Bは直線(1)上の点で、そのx座標は-2である。」
三角形BCOの面積=4×2×1/2=4
ゴールは四角形BODCの面積ですよね
四角形BODC=2+4=6
[関数のまとめ!★]
・問題文を読みながら、数字や文字や式をグラフ上に書き込め
・何を求めているのか、途中も文字や式または単位を書き残していく
・途中で求めた式や座標もその場でグラフに書き込め
・解答する前に、設問のゴール何を求めるのかを再確認する
・求める面積は斜線で強調する
ルールにそって材料を集め、手順を踏みゴールへ向かっていく。メンドくさいね。でも仕事ってこんなものです。学校みたいに穴埋めプリントなんか配ってはもらえない。あなたが自分で、そのメンドウやるから良い給料がもらえるわけです。そこで身に付けた学力はあなたの役に立ちます。必ずです
急がばまわれ、あせらないで!最初は時間がかかりますが、気にせず丁寧に書いていきましょう。 あわてたところですぐに得点まで出来ません。大問の最後の問題は特にね。学校の受験用教材や数友を何度か解くうち、数学のルールにも慣れだんだん速く正確になりますから
カンだけでは出来る仕事は限られます。経験を積むには時間も必要だからね。仕事だってこんな感じで身に付けていくのです。学びにはその時間を縮めてくれるチカラがあります。学べばスタートで差を付けておけます。だから大人はもっと学んでおけばよかったと後悔するんです(藤田)





















