※ この記事は前々回からの続編となりますので、じっくり読み進めたい方は前々回の記事からご覧ください。

・(はじめの7項を調べてみたところ)4,4,2という値の循環が起こっていそう!・・・<要点把握>
↓
・だから(多分)第2003項の1の位の数は4だ!
↓
・どうやって循環が本当に起こっていることを証明する?
↓
・数学的帰納法を使えば証明できる!・・・<実現可能>
以上で、頭の中では問題を攻略できました。
数学を得点源にできる生徒は、頭の中に上の方針が浮かんだ瞬間、
「よし、解けた!」という確信に至ります。
その時点で答案用紙は白紙であっても、勝負はついてしまっているわけです。
『数学的思考』の強化を図った授業では、
問題を攻略するための枠組み(戦略)の構築を重視する分、
具体的な処理や計算は生徒自身に任せる、という姿勢をとることになります。
と言うことは、
『数学的思考』の強化を目指す場合、ある程度の「実践力」をあらかじめ仮定されているわけです。
たとえば
上の問題を授業で扱ったとして、(2)の後半部分の解説を行ったとしたら、
理想として、帰納法の証明は生徒自身の裁量に任せる形になるでしょう。
ですから、帰納法の実践力があらかじめ備わっていなければ、
「思考プロセス」に対する理解は薄れてしまう危険性があります。
「基礎はできるのに、入試問題になると解けなくなる」
「初めて見る問題は解ける気がしない」
と悩んでいる中高生の方へ。
一般に、「思考プロセス」がわかった瞬間は、爽快感に浸れます。
しかし、現状を打破する上で大切なのは「加えて具体的な処理ができるかどうか」です。
できる方にとって「思考プロセス」の強化は最善の方針でしょう。
そうでない場合は・・・
次のことを伝えたいと思います。
「思考プロセス」が分かったからといって、そこで手を止めるべきではない。
具体的な処理がおぼつかないのなら、今の課題は『数学的思考』ではないかもしれない。
思考プロセスと具体的な処理の一挙両得を目指すという戦略は、
本人に相当の合理性が備わっていない限り、どっちつかずの失敗を招きます。
的確な課題は、私たちの言葉でいえば
「深く知る」「知識の融合」であるのかもしれません。
(「自分が該当する」という方へ・・・
この領域での伸び悩みは、伸び悩む要因が多岐にわたります。
上記の内容がすべてではありません。個人の判断が難しい部分ですから、
信頼できる指導者の方に相談されるのが良いでしょう。)
ここまでの総括として、
中高全学年が取り組める、以下の問題をお届けします。
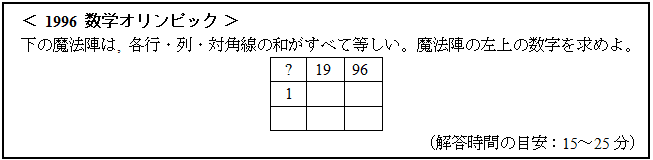
~続く~
(次回の更新は12月4日です)
=============
数学専門塾ヘウレーカ
=============

・(はじめの7項を調べてみたところ)4,4,2という値の循環が起こっていそう!・・・<要点把握>
↓
・だから(多分)第2003項の1の位の数は4だ!
↓
・どうやって循環が本当に起こっていることを証明する?
↓
・数学的帰納法を使えば証明できる!・・・<実現可能>
以上で、頭の中では問題を攻略できました。
数学を得点源にできる生徒は、頭の中に上の方針が浮かんだ瞬間、
「よし、解けた!」という確信に至ります。
その時点で答案用紙は白紙であっても、勝負はついてしまっているわけです。
『数学的思考』の強化を図った授業では、
問題を攻略するための枠組み(戦略)の構築を重視する分、
具体的な処理や計算は生徒自身に任せる、という姿勢をとることになります。
と言うことは、
『数学的思考』の強化を目指す場合、ある程度の「実践力」をあらかじめ仮定されているわけです。
たとえば
上の問題を授業で扱ったとして、(2)の後半部分の解説を行ったとしたら、
理想として、帰納法の証明は生徒自身の裁量に任せる形になるでしょう。
ですから、帰納法の実践力があらかじめ備わっていなければ、
「思考プロセス」に対する理解は薄れてしまう危険性があります。
「基礎はできるのに、入試問題になると解けなくなる」
「初めて見る問題は解ける気がしない」
と悩んでいる中高生の方へ。
一般に、「思考プロセス」がわかった瞬間は、爽快感に浸れます。
しかし、現状を打破する上で大切なのは「加えて具体的な処理ができるかどうか」です。
できる方にとって「思考プロセス」の強化は最善の方針でしょう。
そうでない場合は・・・
次のことを伝えたいと思います。
「思考プロセス」が分かったからといって、そこで手を止めるべきではない。
具体的な処理がおぼつかないのなら、今の課題は『数学的思考』ではないかもしれない。
思考プロセスと具体的な処理の一挙両得を目指すという戦略は、
本人に相当の合理性が備わっていない限り、どっちつかずの失敗を招きます。
的確な課題は、私たちの言葉でいえば
「深く知る」「知識の融合」であるのかもしれません。
(「自分が該当する」という方へ・・・
この領域での伸び悩みは、伸び悩む要因が多岐にわたります。
上記の内容がすべてではありません。個人の判断が難しい部分ですから、
信頼できる指導者の方に相談されるのが良いでしょう。)
ここまでの総括として、
中高全学年が取り組める、以下の問題をお届けします。

~続く~
(次回の更新は12月4日です)
=============
数学専門塾ヘウレーカ
=============



















