近頃の人たちは「算数」というものを嫌う人が多いようだが、昔の日本人は世界的に見ても数学のレベルは相当に高かった。(探究の源流は江戸の寺子屋と和算にあり?社会に開かれた学びと探究心が育てた世界レベルの学力水準!)
何しろ、役人たる武士の子は言うに及ばず、農民の子はコメの取れ高を計ったり商人の子は利幅や値決め、大工の子は寸法の算出の習得にと、それぞれの道に合った和算を相当なレベルで習得していて、数字が生活の大切な要素になっていた。今と違うのは、それぞれ目的をもって学んでいた、ということだ。
中には、「算額」を神社に奉納するほどの数学オタクも結構たくさんいらっしゃったみたいで。(全国算額案内)、(和 算(2013年9月14日)、解く楽しみ(2013年9月21日)、赤とんぼ(2020年10月9日) )

昔から数字は嫌いではない。むしろ、数字への興味はオタクに近いものがあると思っていて、機会があれば、その魅力に触れようとしている。
「数」には、整数とか自然数とか実数とか、いろいろとある訳だが、それを表現する手段の「数字」とは?については、いつの日にか機会があれば触れてみたい。今回は「数式」について見てみたい。
「数式」というものに出会うのは、算数での最初の計算、たぶん、「1+1=2」だろう。
そして次に、「1+2=3」。これは誰でも知っている。
しかしながら、次の様式美を知っている人は少ないようだ。
1+2=3
4+5+6=7+8
9+10+11+12=13+14+15
16+17+18+19+20=21+22+23+24
25+26+27+28+29+30=31+32+33+34+35
36+37+38+39+40+41+42=43+44+45+46+47+48
・・・・・・・・
ずらーっと続く数字の、こういう区切り方で左辺と右辺が同じになるという、こんなにもきれいな算式と出会うこととなる。
要は、行の最初が1、4、9、16・・・と、2乗となっていることにあるのだが、この規則性については何か、あるいは誰かの名前がついていたはずだ。
20より小さい奇数の和がちょうど100になるのも面白い。
1+3+5+7+9+11+13+15+17+19=100
割り算で1を9で割れば、
1÷9=0.11111111・・・・・
と続いていく訳だが、これをもう1回9で割ると、
1÷81=0.012345679012345679・・・・・・
という規則性も見ることができる。「8」が出てこないことが残念でもあるが。
ということで、規則性というものを追求してみると、
1÷9801=
という割り算をエクセルで計算してみる場合、エクセルは小数点以下30桁までが限界みたいだが、結果は
1÷9801=0.000102030405060708000000000000
となって、19桁からは0で誤魔化してしまう。実際には
0.00010203040506070809101112131415161718192021・・・・・95969799000・・・・
ということで、小数点以下3桁以下は01から0203・・と続き、99の手前で98だけが出てこずに、まだまだ違った規則性で続いていく、という物凄い結果となっている。
次は「分数」について。
分数というものを最初に習うのは小学校3年のときらしいが、分母が異なる場合の足し算・引き算については5年生になってからのようだ。
このときのテクニックとして用いられるのが「通分」、つまり分母を同じ値にする訳だが、ここで「最小公倍数」がでてくる時点でつまづくことが多いとのこと。
まぁ、九九をしっかり押さえておけば何なくクリアできるはずのものだが。

で、この「通分」の逆の操作をするのが「部分分数分解」という方法。
たとえば、下記のような計算

それぞれの分数は

と分解されるので、

と打ち消しあうので、
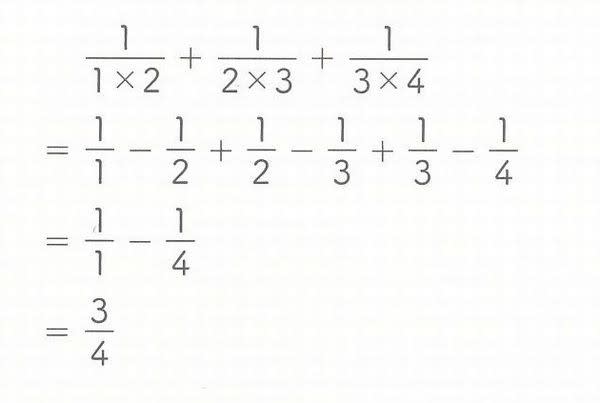
気持ちいいくらいに真ん中が消えていってくれる。が、この「部分分数分解」っちゅうのは、リンク先にも出てるように、きわめて奥が深いので、ここではサラリと触れる程度で止めておく。
対称性のある掛け算の例として、電卓が正常かどうかを証明するときにも使われるのが

その他の対称性の結果など。


累乗にまで広げると更に面白い例がでてくるのだが、際限もなくなりそうなので、2つほど。


今回、参考にした書籍。

数式とは意味を持った文書であり、つまり言葉である、とよく言われる。
言葉は使っていないと忘れてしまうように、数式も使っていないと忘れがちである。
昔、難なく解いた数式も、生活にかまけて使わないでいたら解法さえ忘れてしまっていた。
つまり、数式との会話が困難になってしまっていたわけだ。会話が途絶えることは悲しいので、思い出しながら少しずつ会話ができるように努力している昨今である。
(数学はなんの役に立つなんか聞くんじゃねぇ~数式は言葉編(1)~、数式は言葉編(2) )
ハマス「武器はウクライナから買った」・・・・西側世界から支援されていた武器は横流しされて懐に入り、蓄財や別荘の購入などに化けていた。
イスラエル沖の天然ガスをEUへ運ぶためにはガザが邪魔な西側の私的権力









